5.6 Источники дислокаций Франка-Рида или генераторы
дислокаций
Обычно дислокации возникают при образовании кристалла из расплава или из газообразной фазы. В тщательно отожженном кристалле, т.е. наиболее мягком материале, находится около 106 см-2 дислокаций. В процессе пластической деформации возможны случаи, когда дислокации противоположных знаков, лежащие в одной плоскости скольжения при сближении, уничтожают друг друга. Это явление называется аннигиляция. Если же такие дислокации лежат в разных плоскостях скольжения, то для их аннигиляции требуются дополнительны затраты энергии, связанные с переползанием дислокаций на соседние плоскости. Процесс аннигиляции, а также выход оставшихся в кристалле дислокаций на его поверхность, привели бы к быстрому исчерпанию пластичности материала, и значительная пластическая деформация материала стала бы невозможной, так как имеющиеся в кристалле дислокации были бы израсходованы. Однако, многие материалы, в частности металлы, имеют высокие показатели пластичности. Опираясь на современные представления о металлах, такое явление можно объяснить лишь тем, что в процессе деформирования в кристаллах происходит "размножение" дислокаций в необходимом для пластического течения количестве. Механизм, объясняющий процесс зарождения дислокаций, предложен Франком и Ридом, и поэтому рассматриваемая ниже модель получила распространенное название "источники Франка-Рида" или генераторы дислокаций.
Представим себе плоскость скольжения MN (вид сверху) - рис. 5.12, на которой находится отрезок АВ дислокации.
|
Предположим, что в точках А и В дислокация "намертво" закреплена. Если вдоль плоскости MN действует касательное напряжение τ, то появится сила F = τ·b, действующая на дислокацию. Поскольку дислокации запрещено пе- |
Рис.5.12. Схема источника Франка-Рида |
ремещение в точках А и В, то под действием силы F дислокация постепенно будет прогибаться, направление движения дислокации в каждой точке разное, поскольку сила, действующая на дислокацию, перпендикулярна дислокации. Если приложенное напряжение превышает критическое τmax (положение а на рис. 5.12), то дислокация становится неустойчивой и развивающаяся петля растет, симметрично расширяясь (положение б, в, г) при напряжении τ< τmax. Наконец, обе части зоны сдвига замыкаются (положение г) в точке "С", где встретившиеся дислокации, имеющие противоположный знак, аннигилируют. В результате петля делится на две: образуется полная замкнутая петля дислокации (положение "д") и восстановленный участок АВ, готовый снова изгибаться и давать новую очередную дислокацию в виде петли под действием приложенного напряжения.
Таким образом, источник Франка-Рида, т.е. отрезок дислокации, закрепленный в двух точках, вращаясь, действует непрерывно, как генератор дислокаций и производит замкнутые дислокационные петли, которые, находясь на плоскости скольжения, осуществляют пластическую деформацию этой части кристалла.
Следует заметить, что по наблюдениям экспериментаторов, работа дислокационных генераторов происходит чаще всего вблизи границ зерен (70 – 80 %) и реже в центре кристалла.
Оценим напряжения, которые способны заставить работать источник Франка-Рида.
|
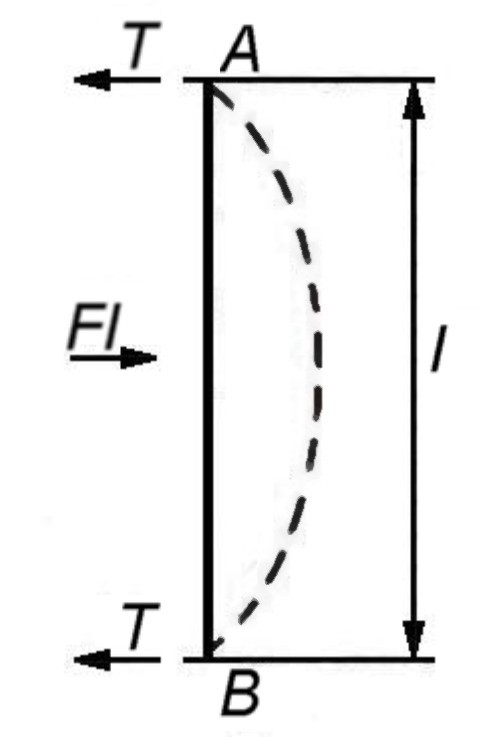
На
рис. 5.13 представлен участок дислокации
АВ
длиной "l".
Положим, что на
нее действует сила Fl
(сила F
действует на единицу длины, а у нас
участок длиной l).
Когда под действием внешней силы
дислокация выгнется, то
в точках А
и
В
появятся реактивные силы Т
или силы натяжения дислокации
(аналогичные силам натяжения), которые
оцениваются уравнением:
|
Рис. 5.13. Силы, действующие на источник Франка-Рида |
.
Можно
записать равенство из условия равновесия:
τ·b·l
= 2T
(т.к. F
= τ·b)
или τ·b·l
= G·b2.
Произведя преобразования, получим
.
Формула определяет величину напряжения, которое необходимо для работы источника Франка-Рида. Видно, что чем меньше l, тем труднее заставить генератор работать - нужны более высокие внешние нагрузки и большая величина напряжения сдвига, действующего в плоскости в которой расположен источник.