
- •Элементы квантовой механики. Физика атомного ядра
- •1.Общие методические указания
- •2.4.Строение атомных ядер, радиоактивность. Закон радиоактивного распада
- •2.5.Элементы дозиметрии ионизирующего излучения
- •2.6. Дефект массы, энергия связи и удельная энергия связи ядра,энергия ядерных реакций
- •3. Примеры решения задач
- •Решение. Определим энергию частицыЕ:
- •4. Задачи для самостоятельного решения
4. Задачи для самостоятельного решения
1. Известно, что фазовая скорость .Найти выражение фазовой скорости волн де Бройля в нерелятивистском и релятивистском случаях.
2. Вычислить наиболее вероятную дебройлевскую длину волны молекул кислорода, содержащихся в воздухе при комнатной температуре.
3. Определить энергиюТ, которую необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от 1 = 0,25 мм до 2 = 0,15 нм.
4. Альфа частица движется по окружности радиусом r = 8,5 мм в однородном магнитном поле напряженностью Н = 20 кА/м. Найти длину волны де Бройля для -частицы.
5. Параллельный пучок моноэнергетических электронов падает нормально на диафрагму с узкой прямоугольной щелью, ширина которой a = 0,06 мм. Определить скорость электронов (считая ее одинаковой для всех частиц), если известно, что на экране, отстоящем от щели на расстоянии L=40 мм, ширина центрального дифракционного максимума b = 60 мкм.
6.Длины волн де Бройля для α-частицы и протона, прошедших соответственно ускоряющие разности потенциалов U1 и U2. одинаковы. Найти отношение величин U1 и U2. Считать, что величины U1 и U2 гораздо меньше энергий покоя частиц.
7.Определить энергиюΔТ, которую необходимо дополнительно сообщить протону, чтобы его дебройлевская длина волны λ= 0,16 нм уменьшилась в 4 раза.
8.Определите, при каком числовом значении скорости длина волны де Бройля для электрона равна его комптоновской длине волны.
9. Электрон обладает кинетической энергией T = 1,5 МэВ. Во сколько раз изменится длина волны де Бройля, если кинетическая энергия T электрона уменьшится в 2,5 раза?
10. Кинетическая энергия T электрона равна удвоенному значению его энергии покоя (2m0c). Вычислить длину волны де Бройля для такого электрона.
11. Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, движущегося внутри сферы радиусом R = 0,05 нм.
12. Используя соотношение неопределенностей, оценить наименьшие ошибки в определении скорости электрона и протона, если координаты центра масс этих частиц могут быть установлены с неопределенностью 1 мкм.
13. Используя соотношение неопределенностей, оценить ширину l одномерного потенциального ящика, в котором минимальная энергия электрона Emin= 15 эВ.
14.Для
приближенной оценки минимальной энергии
электрона в атоме водорода можно
предположить, что неопределенность r
радиуса r
электронной орбиты и неопределенность
p
импульса p электрона
на такой орбите соответственно связаны
следующим образом:
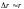 и
и
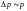 .
Используя эти связи, а также соотношение
неопределенностей, найти значение
радиуса электронной орбиты, соответствующего
минимальной энергии электрона
в атоме водорода.
.
Используя эти связи, а также соотношение
неопределенностей, найти значение
радиуса электронной орбиты, соответствующего
минимальной энергии электрона
в атоме водорода.
15. α-частица находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике.Используя соотношение неопределенностей, оценить ширину l ящика, если известно, что минимальная энергия -частицы Emin = 8 MэB.
16. Принимая, что минимальная энергияЕ нуклона в ядре равна 10 МэВ, оценить исходя из соотношения неопределенностей, линейные размеры ядра.
17. Показать, используя соотношение неопределенностей, что в ядре не могут находиться электроны. Линейные размеры ядра принять равными 510-15 м.
18
Среднее время жизни атома в возбужденном
состоянии составляет
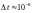 с.
При переходе атома в нормальное состояние
испускается фотон, средняя длина волны
<>
которого равна 600 нм. Оценить ширину
излучаемой спектральной линии, если не
происходит ее уширения за счет других
процессов.
с.
При переходе атома в нормальное состояние
испускается фотон, средняя длина волны
<>
которого равна 600 нм. Оценить ширину
излучаемой спектральной линии, если не
происходит ее уширения за счет других
процессов.
19. Оценить относительную ширину w/w спектральной линии, если известны время жизни атома в возбужденном состоянии (t = 10-8 с) и длина волны излучаемого фотона ( = 0,6 мкм).
20. Во сколько раз дебройлевская длина волны частицы меньше неопределенности х ее координаты, которая соответствует относительной неопределенности импульса р = 1 % ?
21. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими стенками находится в возбужденном состоянии (n = 3). Определите вероятность нахождения частицы в области 3l/7 х 6l/7.
22. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими стенками находится в возбужденном состоянии (n = 2). Определите вероятность нахождения частицы в области l/3 х 2l/3.
23. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими стенками находится в возбужденном состоянии (n = 3). Определите, в каких точках ямы (0хl) вероятность обнаружения частицы: 1) максимальна; 2)минимальна. В каких точках в интервале (0 <х <l) плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Поясните полученные результаты графически.
24.
Частица находится в бесконечно глубоком,
одномерном, прямоугольном потенциальном
ящике. Найти отношение разности
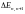 соседних энергетических уровней к
энергии Enчастицы
в трех случаях: 1) n =
2; 2) n =
7; 3)
соседних энергетических уровней к
энергии Enчастицы
в трех случаях: 1) n =
2; 2) n =
7; 3)
 .
.
25.Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l = 0,2 нм. Определить в электрон-вольтах наименьшую разность энергетических уровней электрона.
26. Протон с энергиейЕ= 1 МэВ изменил при прохождении потенциального барьера дебройлевскую длину волны на 1 %. Определите высоту U потенциального барьера.
27. Электрон с энергиейЕ= 100 эВ попадает на потенциальный барьер высотой U = 64 эВ. Определите вероятность W того, что электрон отразится от барьера.
28. Вычислите коэффициент прохождения D электрона с энергиейЕ= 100 эВ через потенциальный барьер высотой U = =99,75 эВ.
29. Прямоугольный потенциальный барьер имеет ширину l = = 0,1 нм. Разность между высотой потенциального барьера и энергией движущегося в положительном направлении осих электрона U–E = 5 эВ. Определите, во сколько раз изменится коэффициент прозрачности D потенциального барьера для электрона, если разность U – E возрастает в 4 раза.
30. Прямоугольный потенциальный барьер имеет ширину l=0,1 нм. Определите в электрон-вольтах разность энергий U–E, при которой вероятность прохождения электрона сквозь барьер составит 0,5.
31. Частица с энергиейЕ= 10 эВ движется в положительном направлении оси х, встречая на своем пути бесконечно широкий прямоугольный барьер высотой U = 5 эВ. Определите коэффициент преломления n волн де Бройля на границе потенциального барьера.
32. Электрон с длиной волны де Бройля 1 = 100 пм, двигаясь в положительном направлении оси х, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 100 эВ. Определите длину волны де Бройля частицы после прохождения барьера.
33. Частица массой m = 10-19 кг, двигаясь в положительном направлении оси х со скоростью υ = 20 м/с, встречает на своем пути бесконечно широкий прямоугольный барьер высотой U = 100 эВ. Определите коэффициент отражения R волн де Бройля на границе потенциального барьера.
34. Частица с энергиейЕ движется в положительном направлении оси х и встречает на своем пути бесконечно широкий прямоугольный барьер высотой U, причем E < U. Принимая А1= 1 и используя условия непрерывности волновой функции и ее первой производной на границе областей 1 и 2, определите плотность вероятности 2(0)2 обнаружения частицы в точке х = 0 области 2.
35. Ширина d прямоугольного потенциального барьера равна 0,2 нм. Разность энергий U–E = 1 эВ. Во сколько раз изменится вероятность W прохождения электрона через барьер, если разность энергий возрастает в n = 10 раз?
36. При какой ширине d прямоугольного потенциального барьера коэффициент прозрачности D для электронов равен 0,01? Разность энергий U–E = 10 эВ.
37. Электрон с энергиейЕ= 9 эВ движется в положительном направлении оси х. Оцените вероятность того, что электрон пройдет через потенциальный барьер, если его высота U = 10 эВ и ширина d = 0,1 нм.
38. Ядро испускает -частицы с энергиейЕ= 5 МэВ. Принимая в грубом приближении, что -частица проходит через прямоугольный потенциальный барьер высотой U = 10 МэВ и шириной d = 5 фм, найти коэффициент прозрачности D барьера для -частиц.
39. Протон и электрон прошли одинаковую ускоряющую разность потенциалов = 10 кВ. Во сколько раз отличаются коэффициенты прозрачности De для электрона и Dрдля протона, если высота U барьера равна 20 кэВ, а его ширина d = 0,1 пм?
40.
Волновая функция, описывающая движение
электрона в основном состоянии атома
водорода, имеет вид
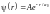 ,
гдеА
– некоторая постоянная; а0
– первый боровский радиус. Найти для
основного состояния атома водорода
среднее значение потенциальной энергии.
,
гдеА
– некоторая постоянная; а0
– первый боровский радиус. Найти для
основного состояния атома водорода
среднее значение потенциальной энергии.
41.
Период полураспада радиоактивного
аргона
 Ar
равен 110 мин. Определить время, в течение
которого распадается 25 % начального
количества атомов.
Ar
равен 110 мин. Определить время, в течение
которого распадается 25 % начального
количества атомов.
42. Радиоактивный изотоп имеет постоянную распада = =4107 с-1. Через какое время распадутся две трети первоначального количества ядер?
43. Радиоактивный изотоп имеет постоянную распада = =8107 с-1. Через какое время останется не распавшейся четверть первоначального количества ядер?
44. За год распалось 60 %некоторого исходного радиоактивного элемента. Определить период полураспада этого элемента.
45.
Определить постоянную распада и число
атомов радона, распавшихся в течение
суток, если первоначальная масса радона
10 г. Период полураспада
 Rn
равен 3,82 суток.
Rn
равен 3,82 суток.
46. Найти период полураспада T1/2 радиоактивного изотопа, если его активность за время t = 10 сут уменьшилась на 24 % по сравнению с первоначальной.
47. Активность A некоторого изотопа за время t =10 сут уменьшилась на 20 %. Определить период полураспада T1/2 этого изотопа.
48.
Определить массу m
изотопа
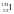 ,
имеющего активность
,
имеющего активность
A = 37 ГБк.
49. Счетчик α-частиц, установленный вблизи радиоактивного изотопа, при первом измерении регистрировал N1= 1400 частиц в минуту, а через время t = 4 ч – только N2 = 400. Определить период полураспада T1/2изотопа.
50.
Определить число N
ядер в радиоактивном изотопе фосфора
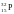 массой
m
= 3 мг, распадающихся в течение времени:
1)t1=
5 мин; 2) t2
= 3 сут.
массой
m
= 3 мг, распадающихся в течение времени:
1)t1=
5 мин; 2) t2
= 3 сут.
51. Определите, при каком числовом значении скорости длина волны де Бройля для электрона равна его комптоновской длине волны.
52. Вычислить толщину слоя половинного ослабления для свинцового экрана, через который проходит узкий монохроматический пучок γ-лучей с длиной волны 0,006∙10-10 м.
53. Какова энергия γ-лучей, если при прохождении через слой железа толщиной в 3,15 см интенсивность излучения ослабляется в 4 раза?
54. Вычислить толщину слоя половинного поглощения свинца, через который проходит узкий монохроматический пучок γ- лучей с энергией 1,2 МэВ.
55. На железный экран падает узкий монохроматический пучок γ- лучей, длина волны которых 0,124∙10-2нм. Найти толщину слоя половинного поглощения железа.
56. Определить для бетона толщину слоя половинного ослабления х½ узкого пучка -излучения с энергией фотонов = 0,8 МэВ.
57. На какую глубину следует погрузить в воду источник -излучения (энергия гамма- фотонов = 1,8 МэВ), чтобы интенсивность пучка, выходящего из воды была уменьшена в k = 1000 раз?
58. Мощность Х экспозиционной дозы, создаваемой удаленным источником -излучения с энергией фотонов = 2 МэВ, равна 0,86 мкА/кг. Определить толщину свинцового экрана, снижающего мощность экспозиционной дозы до уровня предельно допустимой Х = 0,86 нА/кг.
59. На расстоянии l = 10 см от точечного источника -излучения мощность экспозиционной дозы Х = 0,86 мкА/кг. На каком наименьшем расстоянии от источника -излучения экспозиционная доза излучения Х за рабочий день продолжительностью t = 6 ч не превысит предельно допустимую 5,16 мкКл/кг? Поглощением -излучения в воздухе пренебречь.
60. Под действием космических лучей в воздухе объемом V = =1 см3 на уровне моря образуется в среднем N = 120 пар ионов за промежуток времени t = 1 мин. Определить экспозиционную дозу Х излучения,действию которого подвергается человек за время t = =1 сут.
61. Считая, что в одном акте деления ядра урана 235U освобождается энергия 200 МэВ, определить массу m этого изотопа, подвергшегося делению при взрыве атомной бомбы с тротиловым эквивалентом 30∙106 кг, если тепловой эквивалент тротила q равен 4,19 МДж/кг.
62. Найти энергию связи, приходящуюся на один нуклон в ядре атома кислорода О16.
63. Найти энергию связи нейтрона и α-частицы в ядре B11. 64. Найти энергию, необходимую для разделения ядра O16 на четыре одинаковые частицы.
65. Вычислить энергию, необходимую для разделения ядра Ne20 на две α-частицы и ядро С12, если известно, что энергии связи на один нуклон в ядрах Ne20, Не4 и С12 равны соответственно 8,03, 7,07 и 7,68 МэВ.
66. Сколько тепла выделяется при образовании одного грамма Не4 из дейтерия Н2? Какая масса каменного угля с теплотворной способностью 30 кДж/г эквивалентна в тепловом отношении полученной величине?
67. В одном акте деления ядра 235U освобождается энергия 200 МэВ. Определить: 1) энергию, выделяющуюся при распаде всех ядер этого изотопа урана массой m = 1 кг; 2) массу каменного угля с удельной теплотой сгорания q = 29,3 МДж/кг, эквивалентную в тепловом отношении 1 кг урана.
68.
Найти энергию, освобождающуюся при
следующей ядерной реакции:
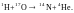
69.
Определить, поглощается или выделяется
энергия при ядерной реакции Определить эту энергию.
Определить эту энергию.
70. Вычислить энергию ядерной реакции:
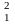 H+
H+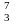 Li
→ 2
Li
→ 2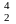 He+
n.
He+
n.
71. Возможна ли реакция He+ 7Li → 10B + n под действием α-частиц с кинетической энергией T = 10 МэВ?
72. Какие ядра могут образовываться в результате реакций под действием: 1) протонов с энергией 10 МэВ на мишени из 7Li; 2)ядер 7Li с энергией 10 МэВ на водородной мишени?
73. Перечислить несколько ядерных реакций, в которых может образоваться изотоп 8Be.
74. При радиоактивном распаде ядер нуклида А1 образуется радионуклид А2. Их постоянные распада равны 1 и 2соответственно. Считая, что в начальный момент времени препарат содержит только ядра нуклида А1 в количестве N10определить промежуток времени, через который количество ядер А2 достигнет максимума.
75. При делении одного ядра 235U освобождается 200МэВ энергии. Какое количество энергии выделится при делении всех ядер 300 г этого изотопа?
76. МощностьP двигателя атомного судна составляет 15 МВт, его КПД равен 30 %. Определить месячный расход ядерного горючего при работе этого двигателя
77.
При бомбардировке дейтроном
H
ядро бериллия
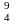 Be
выбрасывает нейтрон. Записать эту
ядерную реакцию и вычислить энергию,
выделяющуюся в ходе реакции.
Be
выбрасывает нейтрон. Записать эту
ядерную реакцию и вычислить энергию,
выделяющуюся в ходе реакции.
78. При
распаде изотопа фосфора
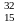 Риз
ядра его атома выбрасывается электрон
и нейтрон. Написать ядерную реакцию
распада изотопа фосфора и определить
число атомов, распавшихся за промежуток
времени, равный 15 дням. Первоначальное
число атомов изотопа N0 = 51020.
Риз
ядра его атома выбрасывается электрон
и нейтрон. Написать ядерную реакцию
распада изотопа фосфора и определить
число атомов, распавшихся за промежуток
времени, равный 15 дням. Первоначальное
число атомов изотопа N0 = 51020.
79. При делении ядра урана 235U под действием замедленного нейтрона образовались осколки с массовыми числами M1= 90 иM2= 143. Определить число нейтронов, вылетевших из ядра в данном акте деления. Определить энергию и скорость каждого из осколков, если они разлетаются в противоположные стороны и их суммарная кинетическая энергия T равна 160 МэВ.
80. Ядерная реакция14N(α,p)17Oвызвана α-частицей, обладавшей кинетической энергией Tα = 4,2 МэВ. Определить тепловой эффект этой реакции, если протон, вылетевший под углом = 60° к направлению движения α-частицы, получил кинетическую энергию T= 2 МэВ.
