Решение. Определим энергию частицыЕ:

.

Так как энергия частицыЕ больше высоты барьера U, то барьер низкий. Определим волновые числа волн де Бройля в областях 1 и 2:

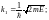
Коэффициент отражения R волн де Бройля через низкий потенциальный барьер бесконечной ширины (Е > U):

,

.

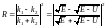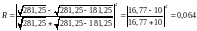Коэффициент пропускания D волн де Бройля через низкий потенциальный барьер бесконечной ширины (Е > U):

=

.

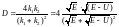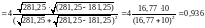Ответ:R = 0,064; D = 0,936.

Задача 5. Электрон с энергиейЕ= 4,9 эВ движется в положительном направлении оси Ох (см. рис. 6.3). Высота потенциального барьера U = 5 эВ. При какой ширине барьера вероятность того, что электрон пройдет через потенциальный барьер, будет равна 0,2?

Решение. Вероятность W прохождения частицы через потенциальный барьер по своему физическому смыслу совпадает с коэффициентом прозрачности D (W = D). Тогда получим:

,

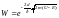где m – масса электрона, d – ширина барьера.

Возьмем логарифм от обеих частей выражения и выразим d:

,

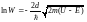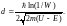
Выразим входящие в эту формулу величины в единицах СИ и произведем вычисления:

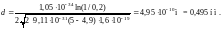
Ответ:d= 0,495 нм.

Задача 6.Определить, сколько ядер в m₀ = 1,0 мг радиоизотопа церия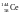 распадается в течение промежутков времени: 1) t = = 1 с; 2) t = 1 год. Период полураспада церия Т_1/2= 285 сут.

Решение. Задача решается с помощью закона радиоактивного распада. Применим две формы записи данного закона исходя из условий задачи.

1. Так как t << T, то можно считать, что в течение всего промежутка t число нераспавшихся ядер остается практически постоянным и равным их начальному числу N₀. Тогда для нахождения числа распавшихся ядер N применим закон радиоактивного распада в виде:

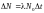, (1)

где –постоянная радиоактивного распада.

2.Выразим величину  из формулы для периода полураспада :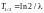

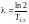. (2)

3.С учетом (2) выражение (1) примет вид:

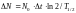. (3)

4. Чтобы определить начальное число ядер (атомов) N₀, умножим постоянную Авогадро N_А на число молей , содержащихся в данном изотопе:

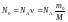, (4)

где m₀ – начальная масса изотопа церия; М – молярная масса церия, численно равная его массовому числу.

5. С учетом (4) получим

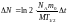. (5)

6. Выразим числовые значения величин, входящих в формулу (5),в единицах СИ: Т_1/2 = 285 сут.24ч3600с = 246,2410⁵ с;N_A= = 6,02 10²³ моль^-1; m₀ = 1 мг = 1,0 10^-6 кг; М =144 г/моль = 0,144 кг/моль.

Произведя вычисление с учетом, что ln 2= 0,693, получим:

.

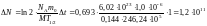8. Рассмотрим случай, когда t = 1 год и величины t и Т_1/2– одного порядка. В этом случае дифференциальная форма закона радиоактивного распада (1) здесь неприменима. Поэтому для решения задачи воспользуемся интегральной формой закона, справедливой для любого промежутка t. Тогда получим:

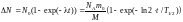. (6)

9. Так кик ехр(ln2) = 2 , то уравнение (6) принимает вид:

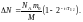(7)

10. Произведем вычисление по (7) с учетом, что 1год = 365 сут:

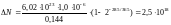
Ответ: 1)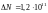 ;2) .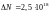

Задача 7.На поверхность воды падает узкий монохроматический пучок γ-лучей с длиной волны 0,775 пм. На какой глубине интенсивность γ-лучей уменьшиться в 100 раз?

Решение.Ослабление интенсивности γ- лучей определяется из формулыJ = J₀e^-μx_, откуда

k = J₀/J = e^-μx, (1)

где J₀– интенсивность падающего пучка γ-лучей; J– их интенсивность на глубине x; μ– коэффициент линейного ослабления.

Решая уравнение (1) относительно x, находим

lnk = μx;x = lnk/μ. (2)

Для определения μ вычислим энергию γ-квантов:

ε = hν = hc/λ, (3)

где h – постоянная Планка; c– скорость света в вакууме.

Подставляя в (3) числовые значения, получим

ε = 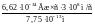= 2, 56∙10^-13Дж = 1, 6 МэВ.

По графику (рис. 6.4) зависимости линейного коэффициента ослабления γ-лучей от их энергии находимμ= 0,06см^-1.

Подставляя это значение μ в формулу (3), находим x =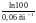 =76,8 см.

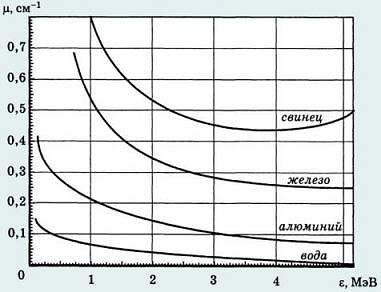
Рис.6.4

Ответ: х = 76, 8 см.

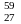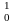Задача 8.Вычислить в мегаэлектронвольтах энергию ядерной реакции Co + n → 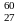Co + γ.Выделяется или поглощается энергия при этой реакции?

Решение.Энергия ядерной реакции равна

∆E=∆mc², (1)

где ∆m– дефект массы реакции; с – скорость света в вакууме.

Если ∆m выражать в а.е.м., то формула (1) примет вид

∆E = 931∆m. (2)

Дефект массы равен:

∆m=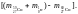 (3)

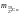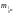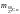Так как число электронов до и после реакции сохраняется, то вместо значений масс ядер воспользуемся значениями масс нейтральных атомов, которые приводятся в справочных таблицах: = 58,95182 а.е.м.; = 1, 00867 а.е.м.; = 59, 95250 а.е.м.;∆m = (59, 96075 – 59, 95250) а.е.м. = 0, 00825 а.е.м.

Реакция идет с выделением энергии, так как ∆m > 0:

∆E = 931 МэВ /а.е.м. ∙ 0,00825 а.е.м. = 7, 66 МэВ.

Ответ:∆E = 7,66 а.е.м.