МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего профессионального образования

«Национальный исследовательский ядерный университет «МИФИ»

Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ

_____________________________________________________________________________

Кафедра физики и микроэлектроники

ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ №2

по дисциплине «СПЕЦГЛАВЫ ФИЗИКИ»

4 семестр

для студентов очной формы обучения

Разработал:

Доцент кафедры «Физика и микроэлектроника» Н.В. Ермолаева

г. Волгодонск, 2012 г.

Общие рекомендации к выполнению индивидуального домашнего задания по дисциплине «Спецглавы физики»

В процессе изучения физики студент должен выполнить индивидуальные домашние задания (ИДЗ) по дисциплине.

Номера задач, которые должен решить студент в ИДЗ, определяются по таблице вариантов. Вариант задания контрольной работы определяется в соответствии с последней цифрой номера зачетной книжки (студенческого билета).

При выполнении ИДЗ следует придерживаться следующих правил.

1. Указывать на титульном листе номер контрольной работы, наименование дисциплины, вариант, фамилию и инициалы студента, шифр специальности, форму обучения.

2. ИДЗ следует выполнять аккуратно, оставляя поля для замечаний рецензента.

3. Задачи своего варианта переписывать полностью, а заданные физические величины выписать отдельно, при этом все числовые величины должны быть переведены в одну систему единиц.

4. Решение задачи и используемые формулы должны сопровождаться пояснениями. В пояснениях необходимо указывать те основные законы и формулы, на которых базируется решение данной задачи.

5. Для пояснения решения задачи там, где это нужно, аккуратно сделать чертеж.

6. При получении расчетной формулы для решения конкретной задачи приводить ее вывод.

7. Задачу рекомендуется сначала решить в общем виде, т.е. только в буквенных обозначениях, поясняя применяемые при написании формул буквенные обозначения.

8. Вычисления следует проводить с помощью подстановки заданных числовых величин в расчетную формулу. Все необходимые числовые значения величин должны быть выражены в СИ.

9. Проверить единицы полученных величин по расчетной формуле и тем самым подтвердить ее правильность.

10. Константы физических величин и другие справочные данные выбирать из таблиц справочников и приложений используемой литературы.

11. При вычислениях использовать микрокалькулятор для более точного расчета.

12. В ИДЗ следует указывать учебники и учебные пособия, которые использовались при решении задач.

13. При предоставлении работы на повторное рецензирование обязательно представлять работу с первой рецензией. Исправленные задачи при повторном предоставлении студентом контрольной работы записываются полностью по вышеприведенным правилам.

Рекомендуемая литература

Основная по лекционному курсу

1. Трофимова Т.И. Курс физики. –14-е изд. Учеб. пособие для вузов. М.: Академия, 2007.

2. Савельев И.В. Курс общей физики: Учебное пособие. В 3-х т. Т.1. Механика. Молекулярная физика. – 9-е изд., стер. СПб.: Лань, 2007. (Учебники для вузов. Специальная литература.)

3. Савельев И.В. Курс общей физики: Учебное пособие. В 3-х т. Т.2. Электричество и магнетизм. Волны. Оптика.– 9-е изд., стер. СПб.: Лань, 2007. (Учебники для вузов. Специальная литература.)

4. Савельев И.В. Курс общей физики: Учебное пособие. В 3-х т.т. Т.3. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц. – 8-е изд., стер. СПб.: Лань, 2007. (Учебники для вузов. Специальная литература.)

Основная к практическим занятиям

1. Трофимова Т.И., Павлова З.Г. Сборник задач по курсу физики с решениями. М.: Высшая школа, 2002.

2.Чертов А.Г., Воробьев А.А. Задачник по физике: Учебное пособие для втузов. – 8-е изд., перераб. и доп. М.: ФИЗМАТЛИТ, 2008.

3.Савельев И.В. Сборник вопросов и задач по общей физике: Учебное пособие для студентов втузов. М.: Астрель (изд-во АСТ), 2005.

Дополнительная литература

1. Волькенштейн В.С. Сборник задач по общему курсу физики. М.: Наука, 1985.

2. Калашников Н.П., Смондырев М.А. Основы физики. В 2-х т. Т.1. М.: Дрофа, 2007.

3. Калашников Н.П., Смондырев М.А. Основы физики. В 2-х т. Т.2. М.: Дрофа, 2007.

Элементы квантовой механики. Физика атомного ядра

Содержание:

1. Общие методические указания…………………………………………………………………стр.1

2. Основные законы и формулы………………………………………………………...................стр.3

   1. Волновые свойства микрочастиц. Фазовая и групповая скорость. Волны де Бройля……...стр. 3

   2. Соотношения неопределенностей Гейзенберга……………………………………………….стр. 3

   3. Уравнение Шредингера. Простейшие случаи движения микрочастиц……………………...стр. 3

   4. Строение атомных ядер, радиоактивность. Закон радиоактивного распада………………...стр. 5

   5. Элементы дозиметрии ионизирующего излучения…………………………………………...стр. 6

   6. Дефект массы, энергия связи и удельная энергия связи ядра, энергия ядерных реакций….стр. 6

3. Примеры решения задач………………………………………………………………………...стр. 6

4. Задачи для самостоятельного решения………………………………………………………...стр.10

1.Общие методические указания

Решение задач контрольных работ является проверкой степени усвоения студентом теоретического курса. Перед выполнением контрольной работы необходимо внимательно ознакомиться с примерами решения задач по данной теме, уравнениями и формулами, а также со справочными материалами. Прежде чем приступить к решению той или иной задачи, необходимо правильно понять ее содержание и поставленные вопросы.

Порядок расположения тем, примеров решения задач и задач для самостоятельного решения в разделе следующий:

1. Волновые свойства микрочастиц. Фазовая и групповая скорость, волны де Бройля.

2. Соотношения неопределенностей Гейзенберга.

3. Уравнение Шредингера. Простейшие случаи движения микрочастиц.

4. Строение атомных ядер, радиоактивность. Закон радиоактивного распада.

5. Элементы дозиметрии ионизирующего излучения.

6. Дефект массы, энергия связи и удельная энергия связи ядра, энергия ядерных реакций.

2.Основные законы и формулы

2.1. Волновые свойства микрочастиц. Фазовая и групповая скорость.

Волны де Бройля.

Фазовая скорость

,

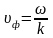где ω– круговая частота; k – волновое число, k = 2/.

Групповая скорость

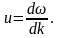
Соотношение де Бройля

,

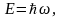
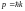где E – энергия движущейся частицы;р–импульс частицы;k – волновой вектор, ; ħ – постоянная Планка,

= .

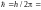
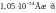2.2.Соотношения неопределенностей Гейзенберга

Соотношение неопределённостей имеет вид:

а) для координаты и импульса частицы

,

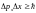где р_х – неопределённость проекции импульса частицы на координатную ось 0x;х – неопределённость её координаты;

б) для энергии и времени

,

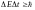гдеЕ – неопределённость энергии данного квантового состояния;t – время пребывания системы в этом состоянии.

2.3.Уравнение Шредингера.

Простейшие случаи движения микрочастиц

Уравнение Шредингера является основным уравнением квантовой механики.

Общее уравнение Шредингера в развернутом виде (временное уравнение):

,

где (x,y,z,t) – волновая функция, описывающая состояние частицы;m – масса частицы; i – мнимая единица;  – оператор Лапласа: ;U – функция потенциальной энергии частицы, включая и энергию в электростатическом поле.

Одномерное временное уравнение Шредингера:

.

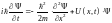Если функция U не зависит от времени, то имеем стационарный случай. В общем случае функция  может быть представлена в виде произведения двух функций:

.

Уравнение Шредингера для стационарных состояний:

.

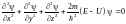Если потенциальная энергия частицы зависит только от одной координаты, например x, то волновую функцию можно искать в виде: 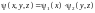. В результате одномерное уравнение Шредингера для стационарных состояний имеет вид:

.

Для волновой функции выполняется принцип суперпозиции: если квантовая система находится в состояниях, описываемых функциями ₁ и ₂, то она может находиться в состоянии

= a₁+b₂,

где а и b – произвольные числа.

Вероятность dW обнаружения частицы в интервале координат от x доx + dx в одномерном случае выражается формулой:

,

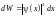где – плотность вероятности.

Вероятность обнаружения частицы в интервале отх₁ дох₂ равна

Рис.6.1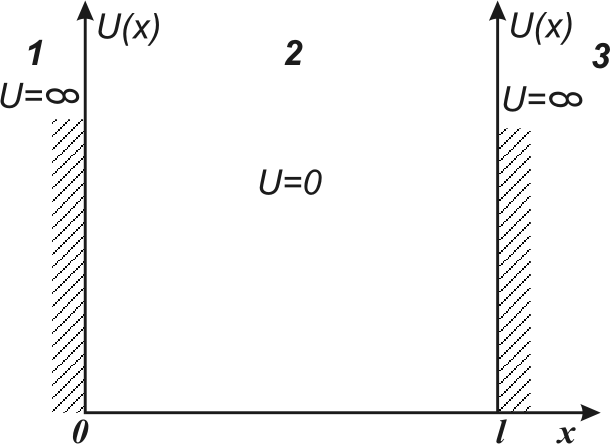

.

Решение уравнения Шредингера для частицы, находящейся в одномерной потенциальной яме с бесконечно высокими (непроницаемыми) стенками (рис. 6.1.), имеет вид:

,

где l – ширина потенциального ящика; n =1,2,3,…

Собственное значение энергии частицы, находящейся на n-м энергетическом уровне: .Если перенести начало координат в точку x =l/2, то в новой системе отсчета волновая функция принимает вид:

Рис.6.2

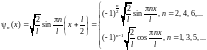
Прямоугольным потенциальным порогом (потенциальной ступенькой) называют силовое поле, описываемое функцией (рис.6.2):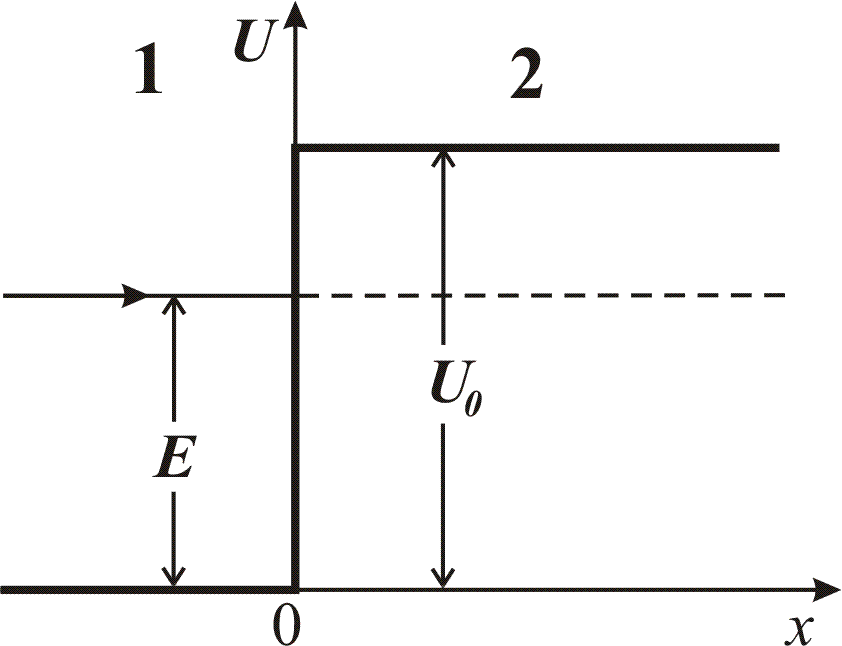

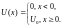
Коэффициент отражения от порога:

.

Отсюда следует, что при E > U₀ существует конечная отличная от нуля вероятность того, что частица отразится от низкого потенциального порога – надпороговое отражение – чисто квантовый эффект. Видно, что при E = U₀ отражение будет полным (R = 1).

Рис.6.3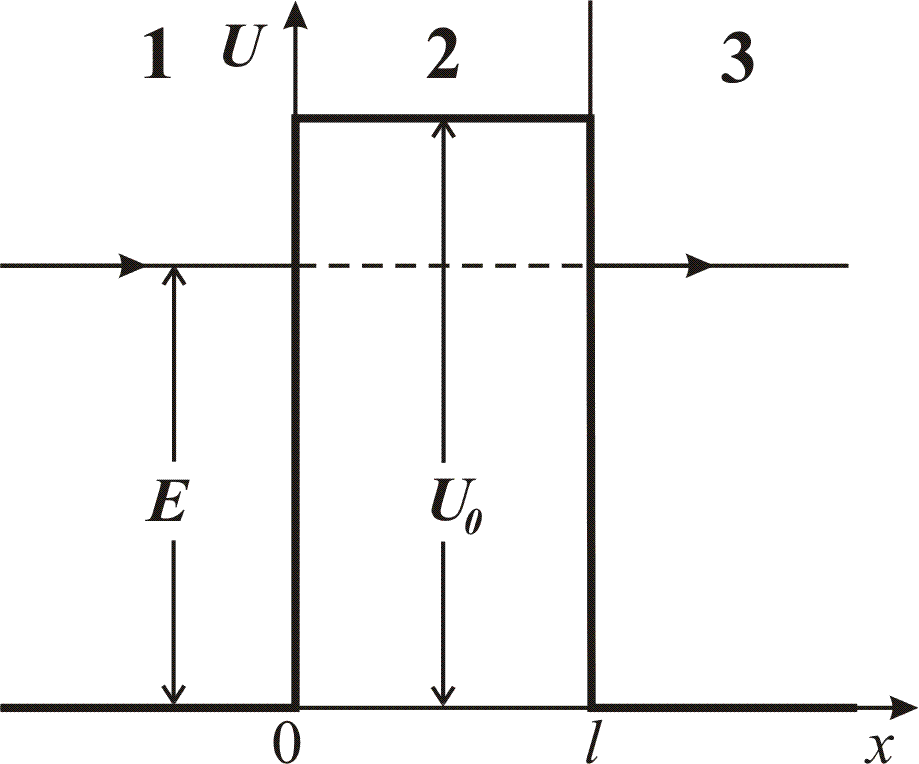

Коэффициента прохождения потенциального порога:

D = 1 – R.

При E > U₀ величину D называют коэффициентом надпорогового прохождения.

Туннельный эффект – это явление прохождения частицы сквозь барьер, когда энергия частицы Е меньше высоты барьера U₀ (в общем случае 0 <E < U₀) (рис. 6.3).

Коэффициент прозрачностиD прямоугольного потенциального барьера конечной ширины равен

,

где D₀(E)– слабо изменяющаяся функция энергииЕ; U₀ – высота потенциального барьера; l – ширина барьера; E – энергия частицы.

Туннельный эффект – чисто квантовое явление, которое можно объяснить только с учётом волновых свойств частиц. При переходе к макрочастицам (m) туннелирование исчезает (D0).

Прозрачность барьера резко убывает с его толщиной; если например U₀–E=5 эВ, то для электрона:

Ширина барьера l, Å	1	1,5	2	5	10
Коэффициент прозрачности D	0,1	0,03	0,008	510-7	1,410-12

Для протона уже при l = 0,1 нмD  2^-100  0.