Ход работы.
1. Включить пересчетный прибор и дать ему прогреться в течение 15-20 мин.
2. Установить необходимое время измерения на приборе (по согласованию с преподавателем, например «3 сек»). Нажать клавишу «Пуск». Через время, установленное на приборе, считать показание прибора. Нажатием клавиши «Пуск» повторить следующее измерение. Таким способом произвести 100 измерений. Результаты измерений занести в табл. 2.
Таблица 2
Результаты измерений
№ измерения |
1 |
2 |
3 |
4 |
5 |
… |
100 |
Число импульсов, N |
|
|
|
|
|
|
|
Обработка результатов.
Результаты измерений (табл. 2) представить в виде таблицы 3.
Таблица 3
k |
|
|
|
|
|
|
|
nk |
|
|
|
|
|
|
|
mk = npk |
|
|
|
|
|
|
|
Здесь k – значения зарегистрированных импульсов (число импульсов),
nk – экспериментальные частоты появления того или иного значения импульса,
mk – ожидаемые по Пуассону частоты.
Для заполнения строки 3 табл.3 необходимо рассчитать выборочное среднее по формуле:
Затем рассчитать p(k) = pk по формуле (3).
4. Найти ожидаемые частоты mk = npk.
5. По формулам (6), (7), (8) рассчитать дисперсию, абсолютную и относительную флуктуации.
5. Вычислить
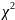по формуле (13).
6. Найти число степеней свободы v по формуле: ν = l−1−t,
где l – число интервалов,
t- количество дополнительных соотношений для оценки параметров распределения p(x) (в нашем случае t =1, т.к. мы используем одно соотношение (14)).
7. С помощью таблицы
1 найти значение
и вероятность α.
Сравнить табличное значение
с вычисленным значением
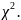
8. Построить экспериментальные nk(k) и теоретические распределения mk(k). 9. На основании полученных результатов п.п.5, 7 и 8 сделать вывод о применимости закона Пуассона к полученному распределению случайной величины и качестве проведенного эксперимента.
Контрольные вопросы.
1. Распределение Пуассона. Условия применимости распределения Пуассона.
2. Дисперсия. Абсолютная и относительная флуктуация случайной величины.
3. Запишите математическое выражение для дисперсии, абсолютной и относительной флуктуации для закона Пуассона.
4. Распределение
.
Проверка гипотез о законе распределения
с помощью критерия
.
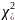