Лабораторная работа № 315 по курсу общей физики, раздел «Ядерная физика» «определение длины пробега альфа-частиц в воздухе»

Цель работы: Цель работы: знакомство с явлением естественной радиоактивности, рассмотрение механизма альфа-распада, получение кривой прохождения α-частиц через вещество (воздух), определение длины среднего пробега и энергии альфа-частиц.

Приборы и принадлежности: установка из двух соединенных кабелем блоков:

1) электронный блок управления и индикации (БУИ), содержащий таймер с максимальным измеряемым интервал времени которого t_max=999 с и блок пересчета импульсов;

2) блок детектирования, состоящий из

- источника и счетчика α-частиц;

- высоковольтного выпрямителя для питания счетчика;

- скамьи со шкалой, по которой перемещается камера с источником на основе ²³⁹Pu.

Рис. 1. Лабораторная установка в сборе, вид общий

Указания по технике безопасности

Источник представляет собой подложку из стали, в углубление которой зафиксирован радиоактивный препарат. Полная активность используемого в лабораторной работе радиоактивного источника – менее 1000 распадов в 1 секунду, что составляет 0,03 мкКи (микрокюри). Это не представляет опасности для здоровья. Кроме того, альфа-частицы, испускаемые источником, не могут пройти сквозь стенки камеры, в которую помещен источник, а только через специальное окно в камере. Несмотря на малую активность радиоактивного источника, запрещается разбирать камеру и доставать источник, трогать его руками и т.п. Попадание радиоактивных веществ на кожу и внутрь организма может привести к появлению внутреннего (внутри тела) источника облучения, который практически невозможно удалить. Также запрещается снимать камеру с источником со скамьи лабораторной установки и направлять окошко источника в глаза.

Теоретическая часть

Наименьшей полной структурной частицей сложного, в общем случае, вещества, сохраняющей все его физико-химические свойства является молекула. В молекуле составляющие ее частицы элементов – атомы – образуют пространственную структуру, которая наряду с составом определяет свойства вещества. Одинаковые по составу, но различные по строению молекулы образуют изомеры – вещества с отличающимися свойствами.

Наименьшей частицей, сохраняющей все свойства химического элемента, является атом.

Атом состоит из положительно заряженного ядра, которое фактически определяет физические свойства элемента, и электронных оболочек, внешняя – валентная – из которых, во многом, определяет химические свойства элемента.

В ядерной физике и в физике элементарных частиц массы часто выражают в единицах энергии, умножая массу частиц (кг в системе SI) на квадрат скорости света в вакууме с² (с=2.997924^.10⁸ м/с)  в соответствии с релятивистской формулой W=m·с². Так, масса частицы, равная 1 МэВ (точнее – 1 МэВ/с²), в системе СИ будет равна 1 МэВ/с² 10⁶Дж/(310⁸ м/с)²1,7810^–30 кг. Выраженная в МэВ масса электрона m_е= 9,1110^–31 кг=0,511 МэВ.

Экспериментально установлено, что любое атомное ядро состоит из нейтронов и протонов, называемых нуклонами.

Протон  квазистабильная (время жизни лет) в свободном состоянии (вне ядра) положительно заряженная элементарная частица с массой покоя m_p=1,67261410^–24 г=938,28 МэВ1836m_e1 а.е.м. и зарядом, равным по величине заряду электрона. Протон  это ядро атома водорода ¹₁Н.

Нейтрон  нейтральная нестабильная свободном состоянии (вне ядра) элементарная частица с массой покоя m_n=1.67439^.10^-24 г=939,57 МэВ1838,6m_e1 а.е.м. (m_n>m_p примерно на 2,5m_е). Вне ядра нейтрон превращается в протон с испусканием электрона и антинейтрино (^-распад)

с периодом полураспада 600–1000 с. В стабильном ядре нейтрон стабилен. По современным представлениям нейтроны и протоны в ядре с огромной быстротой обмениваются виртуальными частицами с массой 200–300m_e, называемых -мезонами или пионами.

Число протонов, равное зарядовому числу Z, определяет положение элемента в Периодической таблице Менделеева, т.е. его название, символ (можно сказать – элемент с Z=92, а можно просто – уран U). Заряд ядра целочисленно кратен наименьшему электрическому заряду одной из немногих стабильных частиц – заряду электрона е=1,602189210^–19 Кл: Z=Ne. Заряд неионизированного атома равен нулю, так как заряд протонов ядра и заряд электронов атома равны. Неионизованный атом – нейтральная частица.

Массовое число А определяет выраженную в атомных единицах массы массу элемента, а также число нейтронов (А-Z) в ядре.

1 а.е.м. = 1,660567^.10^-24 г. - 1/12 массы изотопа (ядра) углерода-12 ¹²С.

Атом с конкретными значениями Z и А ядра называют нуклидом данного элемента. Различают изотопы, изотоны и изобары.

Изотопы – ядра атомов с одинаковым числом протонов Z, но разным числом нейтронов (А-Z), по своим химическим свойствам изотопы одинаковы. Например, у самого тяжелого естественного (встречающегося в природе) элемента – урана много изотопов: , , , , , , у водорода три изотопа: обычный водород или протий , тяжелый водород или дейтерий , и тритий . Обычный водород и дейтерий стабильны, тритий – нестабилен, радиоактивен, его период полураспада около Т_1/2=12,35 года.

Химическим элементом называется множество изотопов с одинаковым зарядом ядра.

Изотоны – ядра с одинаковым числом нейтронов (А-Z), но разным числом протонов Z, например, и .

Изобары – ядра с одинаковым массовым числом А, но разным зарядовым числом Z, например, и , и , , и .

Зеркальные ядра – это ядра, имеющие одинаковое число А. Зеркальные ядра переходили бы друг в друга при гипотетической замене нейтронов протонами, а протонов нейтронами (₃⁷Li и ₄⁷Be). Так как нуклоны (протоны и нейтроны) отличаются изотопическим спином, а сильные взаимодействия свойством изоспиновой инвариантности, то свойства зеркальных ядер близки: они имеют похожие спектры возбуждения с практически одинаковые энергии возбуждения, одинаковые значения спина и т.п.

Экспериментальный размер атома ~10^-8 см, радиус ядра ~10^-13 см оценивается по формуле

,

где А – масса атома (а.е.м.), величина см – оценочный эффективный радиус нуклона.

Заряженное ядро с заключенными в нем более 99,95% массы атома занимает лишь малую часть объема атома и характеризуется огромной плотностью ядерного вещества – оценочно 224 Мт/см³.

Кулоновские силы отталкивания протонов в ядре компенсируются короткодействующими ядерными силами, которые на расстояниях их эффективного радиуса ~10^-13 см превалируют над всеми остальными взаимодействиями. На расстояниях больше 0,5·10^–13 см притяжение сменяется быстро растущим кулоновским отталкиванием. Ядерные силы обладают свойствами насыщения и равнодействия.

Насыщение проявляется в том, что каждый нуклон ядра взаимодействует только с ограниченным числом своих ближайших соседей, а равнодействие – нуклоны одного и разных видов взаимодействуют одинаково (n-n, n-p, p-p) – ядерные силы не зависят от заряда нуклона.

Ядерные силы зависят от взаимной ориентации спинов. Так в ядре дейтерия – дейтроне – нейтрон и протон имеют спины, направленные в одну сторону. При противоположных спинах нейтрон с протоном отталкиваются. Ядерные силы не являются центральными. В частности, это следует из их зависимости от ориентации спинов.

В настоящее время все известные элементарные частицы делятся на два больших класса и особую группу (рис. 2): два класса – сильно взаимодействующих частиц (адроны) и слабо взаимодействующих частиц (лептоны); особая группа – фотоны с характерным для них электромагнитным взаимодействием.

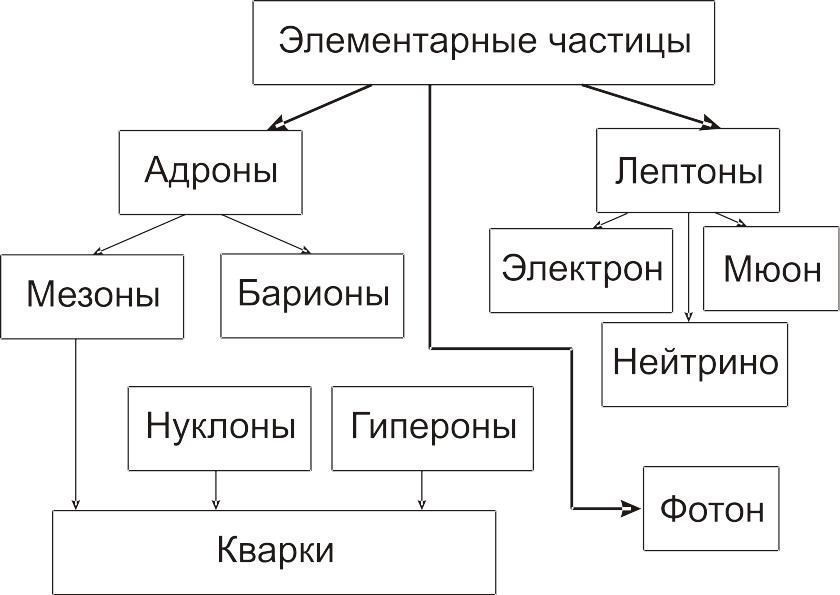
Рис. 2. Общая классификация элементарных частиц

В 1964 г. М.Гелл-Манн и Дж.Цвейг предложили гипотезу, согласно которой все адроны построены из простейших частиц, получивших название кварки, существование которых следует из уравнений физики.

Слово «кварк» взято американским физиком М.Гелл-Маном (Нобелевская премия по физике 1969 г.) из фантастического романа ирландского писателя Дж.Джойса «Поминки по Финнегану»: герою снился сон, в котором чайки кричали тогда еще бессмысленные слова: «Три кварка для мистера Марка».

Согласно этой гипотезе, барионы состоят из трех кварков: u (up – вверх), d (down – вниз), s (strange – странный), антибарионы – из трех антикварков (например, протон имеет кварковую структуру uud, а нейтрон – udd). Эти кварки должны иметь полуцелый спин, их электрический заряд должен быть равным 1/3 или 2/3 заряда электрона (дробный заряд!). В дальнейшем было предположено существование еще трех кварков: с (charmed – очарованный), b (beauty – красивый), t (truth – истинный) с соответствующими антикварками. Комбинации кварков и антикварков дали все известные мезоны. По современным представлениям, кварки лишены внутренней структуры, в этом смысле их можно считать истинно элементарными частицами. Хотя гипотеза кварков оказалась удачной, ибо позволяла с единых позиций объяснить свойства большинства элементарных частиц, кварки в свободном состоянии не были обнаружены, несмотря на многочисленные их поиски на ускорителях высоких энергий, в космических лучах и окружающей среде. Сейчас трудно судить о том, сохранится ли эта гипотеза или ей на смену придет другая.

Особенностью элементарных частиц является их взаимопревращаемость друг в друга. Взаимопревращению элементарных частиц, по современным данным, соответствуют четыре типа физических взаимодействий (перечислены в порядке роста их относительной силы): гравитационное, слабое, электромагнитное, сильное (ядерное). Каждому типу взаимодействий соответствуют свое поле и кванты этого поля, т.е. взаимодействия являются обменными. Говоря иначе, частицы в процессе взаимодействия обмениваются между собой квантами соответствующих полей. Это качество легло в основу объяснения различных видов взаимодействия элементарных частиц как различных проявлений единого взаимодействия. В настоящее время создана единая теория слабых и электромагнитных взаимодействий (электрослабое взаимодействие). Предпринимается попытка создать единую теорию трех видов взаимодействий в микромире: слабое, сильное, электромагнитное («Великое объединение»). Более смелые мечты ученых связаны с поисками возможного Суперобъединения, которое включало бы и гравитационное. В этом случае в единую теорию структуры материи наряду с кварками, лептонами и другими элементарными частицами вошли бы и гравитоны.

Опыт показывает, что масса ядра (целого) m_я меньше, чем суммарная масса образующих ядро нуклонов (частей целого). Разница между суммарной массой свободных нуклонов ядра и массой самого ядра называется дефектом массы ядра . Объяснение этому дает релятивистская механика на основе формулы Эйнштейна, связывающей массу тела с его энергией покоя

.

С другой стороны, рассматривая ядро как систему нуклонов, по этой же формуле имеем

,

где даны массы нуклонов в свободном (вне ядра, несвязанном) состоянии.

Дефектом массы ядра называется разность масс суммы частей и целого

.

,

называемая энергией связи – это часть энергии, которая выделяется при образовании связей в ядре или которую необходимо затратить на разделение ядра на составляющие и удаление нуклонов друг от друга на расстояние, где они не взаимодействуют друг с другом.

Отношение энергии связи к числу нуклонов в ядре называется удельной энергией связи (МэВ/нуклон). Этой величиной удобно характеризовать устойчивость ядер: чем больше удельная энергия связи, тем устойчивей ядро по отношению к радиоактивным превращениям. Для большинства ядер удельная энергия связи почти одинакова в силу свойства насыщения ядерных сил (рис. 3).

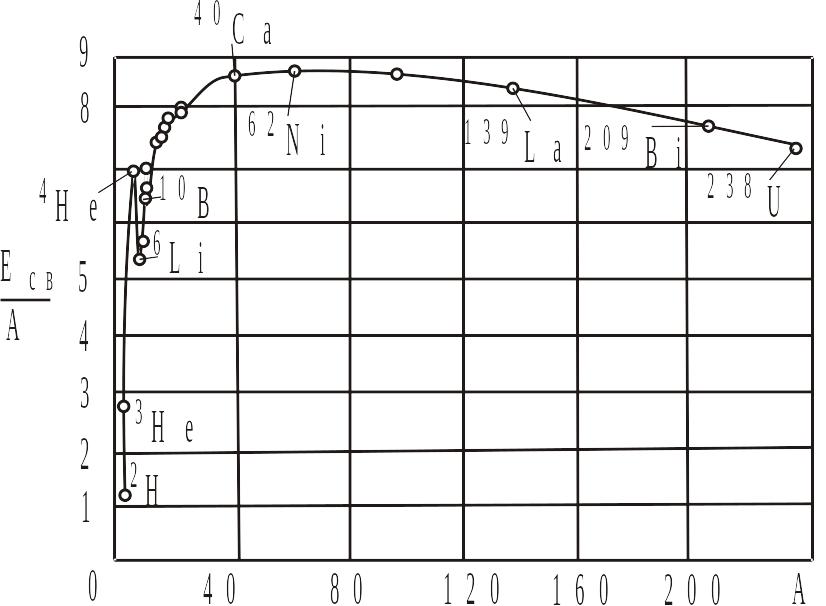
Рис. 3. Зависимость величины удельной энергии связи нуклонов в устойчивых ядрах от величины массового числа

Для легких ядер удельная энергия связи резко возрастает с ростом А. например, для дейтерия  =1,11 МэВ/нуклон, а уже для гелия составляет около =7,07 МэВ/нуклон. Тогда , а разница в энергиях связи МэВ, выделяющаяся в результате реакции синтеза, свидетельствует об энергетической выгодности данной реакции с легкими ядрами (термоядерный синтез при высокой температуре ~10⁶К).

Для ядер с массовыми числами А=50–60 удельная энергия связи максимальна 8,8 МэВ/нуклон (точнее А=56 – железо Fe). С дальнейшим ростом А удельная энергия связи немного уменьшается. Это объясняется возрастающей ролью кулоновского отталкивания для ядер с большим числом протонов.

Нуклоны в ядре подобно электронам в заполненных электронных оболочках могут формировать завершенное (устойчивое) образование – оболочку, характеризуемую магическими числами, речь о которых пойдет далее.

Для урана (А=235 или А=238) удельная энергия связи 7,6 МэВ/нуклон. Например, деление ядра с массовым числом А=240 ( =7,5 МэВ/нуклон) на два одинаковых ядра (деление на два одинаковых осколка маловероятно) с А=120 ( =8,5 МэВ/нуклон) привело бы к высвобождению энергии Е_cв=(8,5–7,5)·240 МэВ=240 МэВ. Для урана эта величина около 200 МэВ, которая, однако, выделяется не просто в виде тепла, а, в основном, в виде кинетической энергии осколков и различных частиц и квантов излучения.

Отсюда следует энергетическая выгодность слияния (синтеза) легких ядер в одно более тяжелое ядро и деления тяжелых ядер на несколько более легких ядер-осколков.

Протон-нейтронное соотношение (A-Z)/А стабильных ядер в природе, равное для легких ядер 1, для тяжелых достигает значения 1,58, отклоняясь от линейного закона роста (A-Z)/А с ростом А в сторону преобладания числа нейтронов над числом протонов. Ясно, что получающиеся при делении тяжелых ядер легкие ядра-осколки пересыщены нейтронами по сравнению со стабильными модификациями ядер и потому всегда радиоактивны.

Существуют множество моделей ядра, рассмотрим кратко лишь самые известные феноменологические (описательные), каждая из которых, тем не менее, является приближенной, описывающей не все, а лишь некоторые свойства ядер. Единой теории, удовлетворительно описывающей все свойства ядер, на данный момент не существует.

Модели ядер делятся на

- одночастичные – нуклон движется в усредненном самосогласованном поле нуклонов ядра, средний его пробег значителен по сравнению с размерами ядра.

- коллективные – нуклоны сильно связаны, их средний пробег много меньше размера ядра, взаимодействует только с ближайшими соседями.

- обобщенные – комбинация одночастичных и коллективных моделей, например, оптическая (ядро – полупрозрачное тело, падающая частица – волна).

Первая и простейшая коллективная модель – капельная (Я. Френкель, Н. Бор) – по аналогии свойств атомного ядра и положительно заряженной капли (механизм деление тяжелых ядер, несферичность ядра и т.д.).

Гидродинамическая или капельная модель ядра была предложена впервые Я.Френкелем и развита Н.Бором в 1939 г. Основное предположение модели: благодаря большой плотности нуклонов и сильному их взаимодействию ядро представляет собой каплю заряженной жидкости плотностью ~10¹⁷ кг/м³. При большой амплитуде колебаний поверхности капли происходит процесс деления ядра. В рамках модели пояснены механизмы ряда ядерных реакций. Модель не объясняет особую устойчивость магических ядер и большинство спектров возбуждения ядер.

В рамках капельной модели ядра атома была получена полуэмпирическая формула для величины энергии связи ядра с заданным А (а.е.м.) и Z – формула Вайцзеккера:

E_св=15,56A-17,23A^2/3-0,71z²/A^1/3-93,46(A/2 -z)²/A + 34A^-3/4 (МэВ),

где последнее слагаемое берется с «+» для чётно-чётных ядер; с «–» для нечётно-нечётных ядер; равна нулю для всех остальных с нечетным А.

Наиболее интересная из одночастичных моделей – оболочечная – заполнение оболочек нуклонами по аналогии с электронами по принципу Паули (существование особо устойчивых ядер). Оболочечная модель ядра разработана в 1940–50 гг. американским физиком М.Гёпперт–Майером и немецким физиком Х.Йенсеном. Основное предположение модели: каждый нуклон движется независимо от других в некотором среднем потенциальном поле (яме), создаваемом остальными нуклонами. В силу сложности задачи функция потенциальной энергии подгоняется под экспериментальные данные. Подобно атомам ядра имеют дискретный спектр энергии с расположением нуклонов по оболочкам. Возбуждение ядра достигается переводом нуклона из занятого нижнего состояния с наименьшей энергией на свободное с большей энергией с учетом принципа запрета Паули для фермионов (протонов и нейтронов).

На величину энергии связи отдельных нуклонов влияет эффект парности: особо прочно связаны в ядре пары протонов и пары нейтронов. Наибольшие значения энергии связи у ядер с четным числом протонов и четным числом нейтронов – так называемые четно-четные ядра (чч). Энергия связи нуклона значительно меньше у нечетно-четных (нч) и четно-нечетных ядер (чн), а самая малая – у нечетно-нечетных ядер.

Замкнутые оболочки нуклонов особенно устойчивы. Если число протонов (нейтронов) ядра совпадает с одним из магических чисел 2, 8, 20, 50, 82 (2, 8, 20, 50, 82, 126), то ядро обладает особой устойчивостью. На магических (для числа протонов или числа нейтронов) или дважды магических числах (и для протонов, и для нейтронов) обычно прекращается ряд распадов тяжелых ядер. Например, ядро свинца ²⁰⁸Pb (Z=82, A–Z=126) является дважды магическим ядром.

Все многоизотопные элементы имеют четные Z, напротив, элементы с нечетным Z, как правило, имеют не более двух изотопов.

Добавочный протон или нейтрон сверх магического числа всегда характеризуется аномально малой энергией связи.

Оболочечная модель противоречит гидродинамической и потому они объясняют «диаметрально» противоположные свойства.

Для коллектива связанных нуклонов, которым является ядро, справедливы по аналогии выводы квантовой механики для энергетического спектра электронов в твердом теле – энергия связанных (в ядре) нуклонов квантуется, при сближении нуклонов на расстояние, близкое к расстоянию между нуклонами в ядре, их спектр становится дискретным, т.е. состоит из разрешенных и запрещенных значений энергии. Переход нуклонов в ядре из их основного состояния на более высокие уровни энергии и составляет процесс возбуждения ядра. Здесь следует провести аналогию с теорией Бора и его постулатами, хорошо известными из общей физики.

Дочерние ядра образуются в возбужденном состоянии, если переход в основное для них запрещен. Для легких ядер А<50 первый возбужденный уровень расположен при энергии ~1 МэВ, а для тяжелых (A>200) – при 0,1 МэВ. При возрастании энергии возбуждения расстояние между уровнями уменьшается. При энергии возбуждения >10 МэВ спектр возбуждения тяжелых ядер становится практически сплошным.

Все энергетические уровни имеют конечную ширину Г (Гτ=ħ, τ – ср. время жизни ядра в данном состоянии), которая определяется на половине высоты (пика) этого уровня.

При переходе из возбужденного состояния в основное при энергии возбуждения

- больше энергии связи нуклона в ядре испускается нейтрон, как не имеющий кулоновского барьера;

- меньше энергии связи нуклона в ядре испускается гамма-квант или электрон конверсии (с внутренних оболочек атома – K-, L-, M- и т.п. электроны).

Явление изомерии было открыто в 1921 г. Отто Ганном. Ядра в метастабильном возбужденном состоянии и основном энергетическом состоянии называются изомерами, а метастабильный уровень – изомерным уровнем. Среднее время жизни гамма-активных ядер обычно 10^-11–10^-7 с. Метастабильный уровень – уровень ядра с гораздо большим временем жизни, обычно имеющий с основным большую разницу в спинах, что сильно затрудняет переход ядра из метастабильного в основное состояние: (изомерный переход). Изомерный уровень обычно характеризуется малой энергией возбуждения (рис. 4).

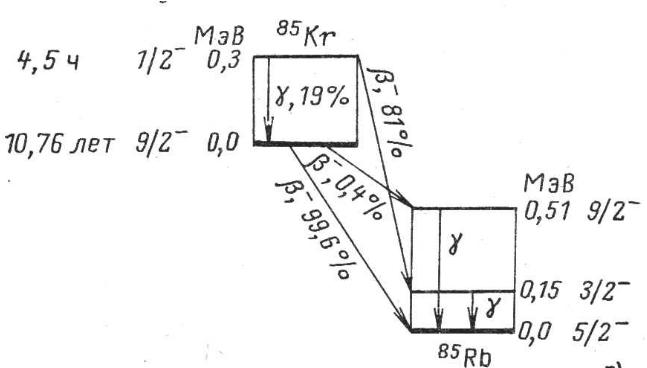
Рис. 4. Изомерный переход

Радиоактивностью называют свойства атомных ядер самопроизвольно превращаться в другие ядра (изменяя Z и А) путем испускания элементарных частиц и различных видов излучения. При одних и тех же закономерностях процессов различают радиоактивность естественную (фон природных неустойчивых изотопов) и искусственную (при инициируемых ядерных реакциях, трансурановые элементы).

Радиоактивный распад происходит

• из-за избыточности в ядрах числа нейтронов или протонов по сравнению с равновесным соотношением числа нейтронов и протонов в устойчивых ядрах того же нуклида (рис. 5): при Z>20 N/Z отклоняется от 1 и для последнего стабильного изотопа ₈₃²⁰⁹Bi достигает N/Z=1,52;

• из-за избыточности энергии у нуклонов ядра по сравнению с их энергией в стабильном ядре.

Закон радиоактивного распада дает зависимость числа радиоактивных ядер от времени N(t). Так как отдельные радиоактивные ядра распадаются независимо друг от друга, можно считать, что число ядер dN, распадавшихся в среднем за интервал времени от t до t+dt, пропорционально числу ядер N(t), имеющихся в момент времени t и промежутку времени dt: , где λ – постоянная радиоактивного распада данного вида, знак «–» указывает на то, что число ядер уменьшается. Разделим переменные и проинтегрируем 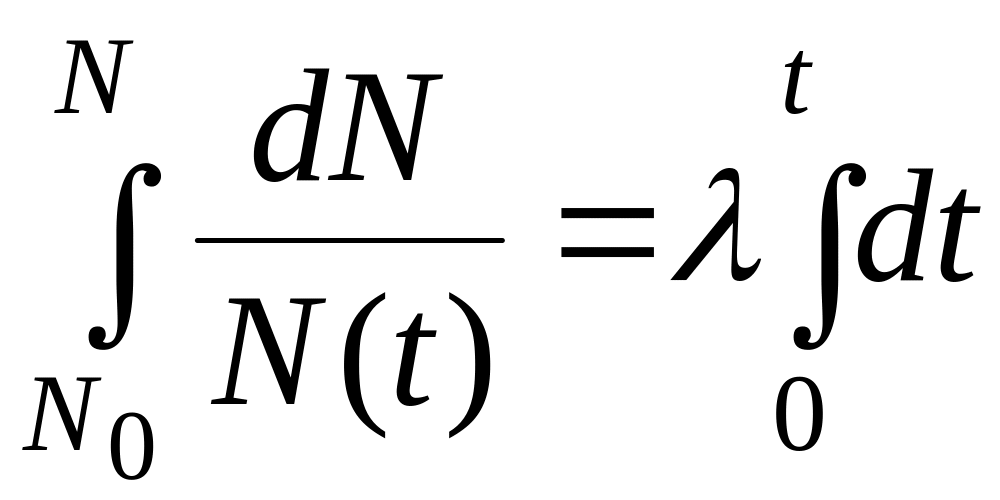, тогда получим закон радиоактивного распада, справедливый для всех видов распада

,

где N₀ – число радиоактивных ядер при t=0.

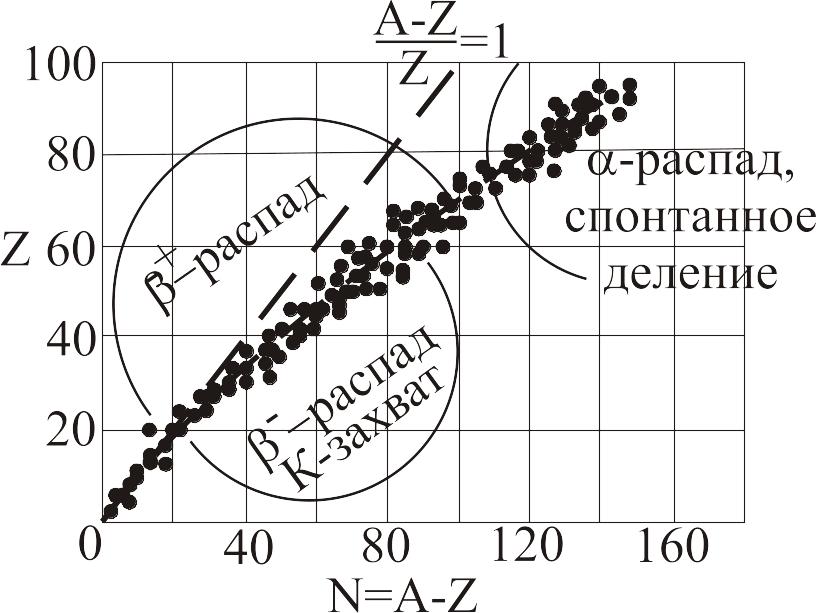
Рис. 5. Виды радиоактивного распада (точки – область стабильных изотопов)

Для того, чтобы узнать количество распадавшихся за время t ядер N_расп, надо из начального числа ядер N₀ вычесть число ядер, оставшихся спустя время t:

.

Периодом полураспада Т_1/2 называется время, за которое распадается половина первоначального количества ядер (изменяется в широких пределах от 3·10^–7 с до 5·10¹⁵ лет). Согласно закону N(t)=N₀/2 при t=Т_1/2, следовательно , откуда

.

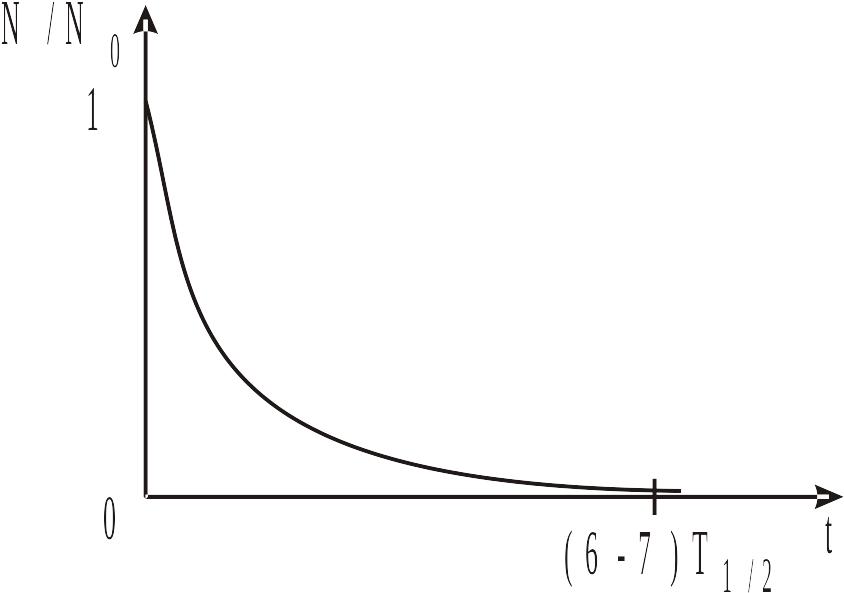
Рис. 6. Экспонента радиоактивного распада

Теоретически, экспонента в законе радиоактивного распада – функция, убывающая до нуля за бесконечное время (рис. 6). Фактически, основная масса радиоактивных ядер распадается до 1% за период времени, равный 6–7 полупериодам Т_1/2 или 4–5 периодам экспоненты Т=1/λ≈1,44 Т_1/2.

Если радиоактивный нуклид 2 появляется вследствие распада материнского нуклида 1, то

,

, а .

Радиоактивное (вековое) равновесие наступает при условии равенства скоростей распада материнских (или рождения дочерних ядер) и распада дочерних ядер: .

Для грубых оценок постоянной распада используется ее связь с пробегом -частиц в воздухе, устанавливаемую законом Гейгера–Нэттола (1911 г.): чем больше постоянная распада радиоактивного элемента, тем больше пробег R_ в воздухе испускаемых им -частиц

, (18.6^/)

где А и В – опытные постоянные, причем В – одинаково для всех радиоактивных семейств.

По другому, закон Гейгера–Нетолла через период полураспада T_1/2 α-радиоактивного ядра и энергию E_α испускаемой им α-частицы можно записать в виде

,

где постоянная C₁ одинакова для всех радиоактивных семейств, а постоян­ные C₂ отличаются одна от другой примерно на 5%. Эти постоянные являются эмпирическими, то есть определяются из эксперимента.

Активностью радиоактивного вещества а называется число распадов в единицу времени, измеряется в беккерелях: 1 Бк=1 распад/с, внесистемная единица – кюри, 1 Ки=3,7·10¹⁰ Бк. С учетом закона радиоактивного распада имеем:

.

Используя связь постоянной распада λ и периода полураспада Т_1/2, выражение для активности радиоактивного вещества примет вид:

.

Так как все виды распада имеют вероятностный характер, то их принято изображать в виде схем, приведенных на рис. 4.

Возникающие в результате радиоактивного распада ядра часто тоже оказываются радиоактивными. В результате возникает целый ряд радиоактивных превращений (семейство), заканчивающихся стабильным элементом. В настоящее время обнаружено четыре радиоактивных ряда (семейства), начинающихся с тория , двух изотопов урана и и нептуния . Эти ряды заканчиваются соответственно стабильными изотопами свинца  для тория и и для изотопов урана, стабильным ядром висмута для нептуния.

Типичным примером -радиоактивного распада является реакция

(Q – энергия).

Обобщенная формула -радиоактивного распада материнского X-ядра в дочернее Y-ядро при испускании -частиц (ядер гелия):

.

Главными характеристиками α-радиоактивных ядер и испус­каемых ими α-частиц являются период полураспада T_½, кинетическая энергия T_α и пробег R_α. Существуют следующие основные закономерности и особенности α-распада.

Выявлена сравнительная узость границ возможных значений анергии α-частиц радиоактивных ядер и очень большой разброс в значениях их периодов полураспада. За очень небольшими исключениями, энергия α-частиц T_α и периоды полураспада T_½ для всех из­вестных в настоящее время α - радиоактивных ядер заключены в пределах

Как правило, α-радиоактивностью обладают ядра с за­рядом Z>82 (тяжелее свинца), причем энергия α-частиц растет с ростом Z ядра. Исключениями являются несколько ядер ред­коземельных элементов (например, , и др.), а также некото­рые искусственно полученные ядра с большим недостатком ней­тронов. Для редкоземельных элементов энергия α - частиц значительно меньше, а период полураспада больше, чем для тяжелых (на­пример, имеет T_α = 1,8 Мэв и T_½ = 5·10¹⁵ лет).

При сравнении энергии α-распада E_α различных изотопов одного и того же элемента наблюдается закономерное уменьше­ние энергия с ростом массового числа. Особенно чет­кая картина получается для четно-четных ядер. Детальный анализ этой закономерности показывает, что она справедлива при A>215 и A<209 и нарушается при промежуточных значениях массового числа. Эта закономерность помогает предсказать энер­гию α-частиц для неизвестных изотопов данного элемента.

Открыта так называемая тонкая структура α-спектров. Оказалось, что обычно ядра испускают α-частицы не с одним, а с несколькими близкими значениями кинетиче­ской энергии. Было за­мечено, что наибольшее число линий тонкой структуры встречается у α-спектров таких ядер, дочерние ядра которых обладают ярко выраженной не сферичностью, и что при прочих равных условиях α–частицы с меньшей энергией испускаются с меньшей интенсивностью.

Мерой прочности (устойчивости) ядра относительно разделения его на какие-либо составные части является величина энергии связи ядра относительно этих частей. Чем больше энергия связи, тем труднее произвести разделение. Если энергия связи отрицательна, ядро может разделиться самопроизвольно, причем этот процесс будет сопровождаться выделением энергии, равной модулю энергии связи. В соответствии с этим условие энергетической возможности α-распада (условие возможности осуществления a-радиоактивного распада) можно записать следующим образом:

или

,

.

Энергия и масса материнского ядра больше суммарной массы дочернего+-частица, соответствующая разница энергий выделяется в виде кинетической энергии дочернего ядра и -частицы и изучения -квантов при переходе дочернего ядра из возбужденного состояния в нормальное. Иногда -квант может не покидать ядро, а передать энергию электрону одной из внутренних электронных оболочек, в результате чего электрон покидает атом (внутренняя конверсия). На освободившееся место переходит другой электрон с испусканием кванта рентгеновского излучения, являющегося характеристическим.

Избыток энергии исходного ядра выделяется при α-распаде ядра в виде кинетической энергии. Подавляющую часть кинетической энергии, вы­деляющейся при α-распаде, уносит α-частица, и лишь незначи­тельная ее доля (~2% для тяжелых α-радиоактивных ядер) приходится на ядро-продукт.

Итак, при a-распаде около 90 % энергии передается a-частице, остальное – ядру отдачи, которое после этого часто оказывается в возбужденном состоянии и практически сразу испускает избыток энергии в виде гамма-кванта (или электрон конверсии). a-частица, испускаемая каждым видом ядер, характеризуется конкретными значениями энергии, свойственными только этим ядрам – это разница энергий материнского и дочернего!

Считается, что a-частица образуется из нуклонов при выходе из тяжелого ядра, при этом ее характеристики зависят от структуры оболочек ядра (несферичности ядра), кулоновского барьера при вылете, от момента, уносимого самой a-частицей и т.п.

Энергетическое рассмотрение α-распада позволило объяснить целый ряд экспериментальных закономерностей этого процесса. Непонятной осталась только природа закона Гейгера–Нэттола, который никак не следует из энергетической схемы α-распада. Согласно энергетической схеме, α-распад становится возмож­ным в том случае, когда ε_α<0, т.е. когда энергия исходного ядра больше суммы энергий ядра-продукта и α-частицы. Но если это так, то почему α-распад не происходит мгновенно (т. е. за время τ = R/v, где R - радиус ядра, а v – скорость α-частицы)?

Можно сказать, что процесс альфа-распада делится на две стадии: образование в ядре виртуальной устойчивой из-за насыщения ядерных сил (2 протона и 2 нейтрона) -частицы и испускание ее ядром. Для того, чтобы покинуть ядро -частица должна преодолеть потенциальный барьер, величина которого, как показывает опыт, много больше максимальной энергии покидающих ядро -частиц.

Дело в том, что потенциальная энергия α-частицы при r=R имеет максимум, который называется кулоновским потенциальным барьером. Поэтому нет ничего удивительного в том, что α-распад происходит не мгновенно. Объяснение природы α-распада заключается именно в этом, неправдоподобном с точки зрения классической физики, эффекте преодо­ления потенциального барьера. В мире ми­крочастиц (электронов, нуклонов, α-частиц), движение которых описывается не классической, а квантовой механикой, возможен процесс так называемого туннельного перехода – прохожде­ния частицы через потенциальный барьер. Соответствующая задача была решена в квантовой механике (Гамов, 1928). Решение получается в виде выражения для коэффициента прозрачности барьера D. Величина коэффициента прозрачности потенциального барьера D имеет физический смысл вероятности для α-частицы пройти через потенциальный барьер.

В результате говорят о туннелировании -частиц через потенциальный барьер, по оценкам лишь одна из 10³⁶ попыток -частицы вырваться (туннелировать) является успешной.

Возникающие альфа-частицы взаимодействуют с веществом посредством упругого рассеяния и ионизационного торможения. При упругом рассеянии суммарная кинетическая энергия частиц сохраняется и перераспределяется между ними. Вследствие большой массы (М_α=7350 m_e, m_e – масса электрона) альфа-частицы почти не рассеиваются на электронах среды (а только на ядрах), продолжая двигаться прямолинейно (Рис. 7.).

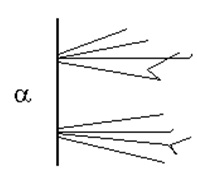
Рис. 7. Схемы движение альфа-частиц при рассеянии

Кулоновское поле электронов атомов вещества взаимодействует с движущейся α-частицей, которая при этом теряет энергию, постепенно останавливаясь. Это процесс ионизационного торможения. Характерной особенностью альфа-частиц является существование у них определенного пробега R – расстояния, которое проходит частица до момента полной потери энергии. Точные расчеты удельных ионизационных потерь энергии для релятивистских заряженных частиц дают следующий результат (формула Бете–Блоха):

,

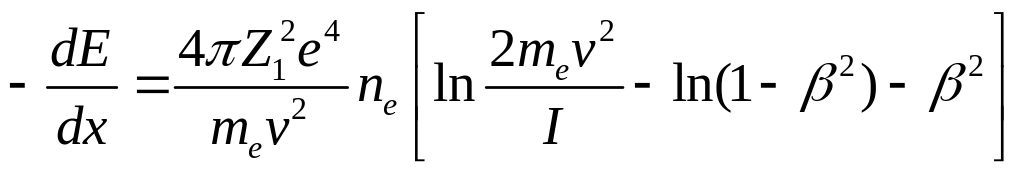где и заряд налетающей частицы и ядра, соответственно, - средний ионизационный потенциал атомов вещества среды, через которую проходит частица, эВ, , , – концентрация атомов вещества.

Таким образом, удельные потери энергии пропорциональны числу электронов вещества и квадрату заряда частицы теряющей энергию на ионизацию. Удельные потери энергии не зависят от массы проходящей через вещество частицы, но существенно зависят от скорости частицы. Например, мюоны гораздо тяжелее электронов, поэтому при той же энергии они теряют ее медленнее, чем электроны и проходят сквозь большие слои вещества без существенного замедления. Удельные потери энергии возрастают с уменьшением энергии частицы и особенно резко перед ее остановкой в веществе (так называемый пик Брэгга).

Для определенной среды и частицы с данным зарядом величина является функцией только кинетической энергии. Учитывая этот факт, можно вычислить полный пробег частицы, то есть путь , который заряженная частица проходит до остановки и полной потери кинетической энергии:

.

Тяжелые заряженные частицы взаимодействуют в основном с атомными электронами и поэтому мало отклоняются от направления своего первоначального движения. Вследствие этого пробег тяжелой частицы измеряют расстоянием по прямой линии от точки входа частиц в вещество до точки их остановки. Обычно пробег измеряется в единицах длины или длины, умноженной на плотность (г/см²).

Таким образом, потеря энергии на ионизацию пропорциональна массовой толщине поглотителя и не зависит от его природы:

.

Если исследовать монохроматический поток α-частиц и подсчитывать число частиц, увеличивая постепенно расстояние между источником и детектором, то есть заставляя альфа-частицы проходить все больший слой воздуха, то число N частиц в пучке начинает на определенном расстоянии падать не сразу до ноля, а с некоторым наклоном (кривая 1 на Рис. 8).

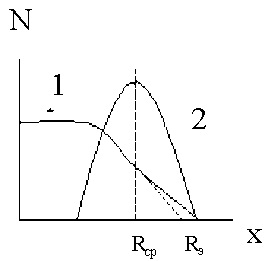
Рис. 8

Если эту кривую продифференцировать и построить величину dN/dx в зависимости от толщины слоя x , то получится кривая 2 (Рис. 8) с резким максимумом при x=R_ср, показывающим, что подавляющее большинство α-частиц имеет определенный пробег с некоторым разбросом в ту и другую сторону. В диапазоне энергий 4<E_α<15 Мэв используют для оценки E_α зависимость:

. (1)

Для Е_α<4 МэВ связь между пробегом и энергией частицы представлена в виде номограммы (рис. 9), при помощи которой по пробегу частицы можно найти ее энергию, и наоборот. Иногда для оценки E_α используют R_э – экстраполированный пробег, полученный путем продолжения наклонной линии 1 до пересечения с осью абсцисс.

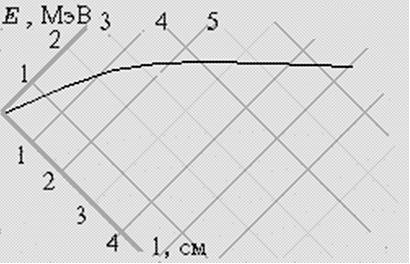
Рис. 9. Номограмма: связь между пробегом и энергией частицы

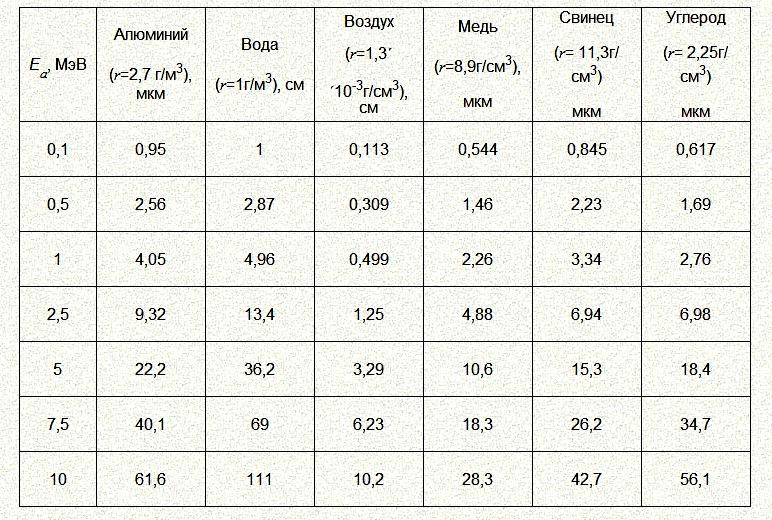
Рис. 10. Пробеги альфа-частиц в веществах

Для построения кривой N(x) необходимо внести поправку на телесный угол с учетом реальных размеров окон детектора и источника, так как в детектор попадает лишь часть излучения.

Увеличение расстояния уменьшает телесный угол, в котором счетчик «видит» испускаемые частицы, и приводит к уменьшению регистрируемых частиц. Для получения полного числа частиц надо зарегистрированное число частиц поделить на поправку, взятую из таблицы 1.

Таблица 1. Поправка на телесный угол

x/r0	0.1	0.2	0.4	0.5	0.6	0.8	1.0	1.25	1.5
Поправка	0.286	0.253	0.197	0.175	0.158	0.127	0.102	0.080	0.062

где x – расстояние между окном детектора и α-препаратом (задаваемое в опыте), r₀=9,8 мм – эквивалентный радиус окошка детектора.

Таблица 2. Краткая информация об альфа-излучении некоторых актиноидов

Нуклид	Период полураспада, Т1/2, лет	Энергия α-частиц, Еα, кэВ	Выход α-частиц, Iа, %
228Th	1,91	5340±1 5423+1	27,6±0,9 71,7±0,9
232Th	1,4 1010	3953±2 4010±3	22±3 77±3
233U	1,6 105	4824+1	84±3
234U	2,46 105	4723+1 4775+1	28,4+0,1 71,4±0,1
234U	7,1 10б	4368±10 4396+3	15±3 55±3
238U	4,5 109	4150±5 4198±5	23+4 77+4
238Рu	87,74	5456±1 5496±1	28,8+0,1 71,6±0,1
239Рu	2,4 104	5106±1 5145±1 5157±1	11,4±0,2 15,1+0,2 72,7±0,2
240Рu	6,5 103	5123±1 5168±2	27,0+0,5 73,0±0,5
241Аm	432,2	5442,9±0,1 5485,6±0,1	12,8±0,2 85,2±0,8
242Сm	0,44	6069±1 6113±1	25,9±0,5 74,1 ±0,5
244Сm	18,1	5763±1 5805±1	23,6+0,3 76,4±0,2

Дискретный характер α-излучения дает возможность проводить количественный анализ содержания радионуклидов с помощью спектрометрических измерений.

На присутствие α-излучающих радионуклидов могут указывать три признака:

- испускание α-частиц;

- испускание нейтронов, возникающих в результате (α, n)-реакций на легких ядрах (Be, F, О, С, А1), присутствующих в образце;

- разогрев образцов в результате торможения α-частиц в их объеме.

²³⁸Рu является практически важным изотопом плутония. Несмотря на его относительно малую концентрацию (табл. 3), он вносит значительный вклад как в тепловыделение, так и в нейтронное излучение образцов плутония. Данные о содержании ²³⁸Рu в образце необходимы для расшифровки результатов анализов, выполненных методом калориметрии или счета нейтронных совпадений.

Таблица 3. Изменение изотопного состава плутония с ростом выгорания

Изотоп	Содержание изотопа в Pu
238Pu	0,0024	0,012	0,20	0,65
239Pu	97,96	93,82	82,49	67,01
240Pu	2,01	8,90	13,75	21,80
241Pu	0,02	0,24	2,69	8,11
242Pu	0,003	0,02	0,76	2,44

Для неразрушающего определения содержания изотопа ²³⁸Рu в плутонии используют γ‑спектрометрию (например, программы MGA и FRAM), для разрушающих – масс-спектрометрию или α-спектрометрию. Разрушающие анализы проводятся в следующих случаях:

- для проверки результатов неразрушающих измерений;

- для проведения особо важных контрольных измерений;

- для аттестации стандартных образцов.

С использованием неразрушающих анализов также контролируют технологические процессы, в которых ЯМ находятся в балк-форме, и нет необходимости специально применять разрушающую процедуру.

Часто масс-спектрометрические измерения изотопного состава образцов плутония дополняются α-спектрометрическими анализами ²³⁸Рu. Так поступают в случаях, когда содержание Рu мало для проведения точного масс-спектрометрического анализа, или когда он интерферирует с ²³⁸U из-за загрязнения масс-спектрометра или образца ураном.

Поскольку типичное отношение уран/плутоний в выгоревшем топливе составляет примерно 100:1, а концентрация ²³⁸Рu не превышает 1%, для выделения плутония требуется химическое разделение с коэффициентом очистки порядка 10⁴. Следует помнить, что результаты масс-спектрометрических измерений Рu очень чувствительны к присутствию даже малого количества урана, оставшегося в образце в результате неполного разделения.

Даже при концентрации ²³⁸Рu 0,01-0,7% (массовых) его вклад в активность достаточно заметен по сравнению с остальными изотопами плутония. Например, если образец содержит 0,15% Рu, 86% ²³⁹Рu и 11,5% ²⁴⁰Рu, то около 25% общей α-активности составляет активность ²³⁸Рu. Удельная α-активность ²⁴¹Рu и ²⁴²Рu настолько мала, что ею можно пренебречь даже в том случае, когда содержание каждого из них достигает 10% (по массе).

α-пики ²³⁸Рu с энергиями 5,50 и 5,46 МэВ хорошо отделяются в спектре от группы пиков ²³⁹Рu и ²⁴⁰Рu, находящихся в интервале энергий 5,11÷5,17 МэВ. α-пики ²³⁹Рu и ²⁴⁰Рu в этой группе, как правило, невозможно разделить.

Плутониевый источник для α-спектрометрических измерений изготовляют следующим образом. Порцию раствора, содержащего плутоний, разбавляют азотной кислотой. Аликвоту разбавленного раствора экстрагируют вместе с эквивалентным объемом ТОФО (триоктилфосфиноксида) в ксилоле. Часть органической фазы выпаривают на счетный диск. В других случаях плутониевую фракцию можно отделить и очистить с помощью ионообменной процедуры, а аликвоту очищенного раствора выпарить на подложку (счетный диск).

Присутствие в источнике инертного остатка может привести к поглощению α-частиц и деградации α-спектра.

Для изготовления α-источников с тонким и равномерным слоем радиоактивного вещества применяют и другие способы: испарение в вакууме, катодное или лазерное распыление и др. Счетный диск изготовляется из хорошо отполированной металлической или стеклянной пластины. Обычно он имеет диаметр 25 мм, толщину 0,05 мм, в центре углубление диаметром 4 мм. Завершающие процедуры изготовления источника включают выравнивание слоя органического осадка и выжигание органической компоненты счетного слоя.

²⁴¹Am должен быть предварительно удален из образца, потому что его α-излучение может накладываться на излучение ²³⁸Рu.

Поскольку измеряется отношение ²³⁸Pu/(²³⁹Pu+²⁴⁰Pu), нет необходимости знать количество плутония в источнике. Содержание Рu рассчитывается из отношения его α-активности к полной α-активности источника, а относительное содержание ²³⁹Рu и ²⁴⁰Рu определяется с помощью масс-спектрометрии отдельного образца того же раствора плутония.

Изотопное отношение R_8/9=²³⁸Pu/²³⁹Pu можно вычислить следующим образом:

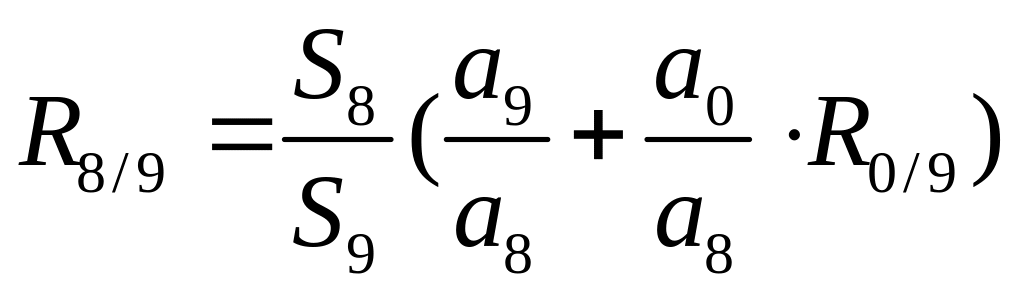(2)

где получают с помощью масс-спектрометрии;

-  измеренное число отсчетов в суммарном пике 5,50 и 5,46 МэВ;

- измеренное число отсчетов в области пиков ²⁴⁰Рu и ²³⁹Рu с энергией 5,11-5,17 МэВ;

= 3800 10⁷ расп./(мин. мкг) - удельная α-активность ²³⁸Рu;

= 1,376 10⁵ расп./(мин. мкг) - удельная α-активность ²³⁹Рu;

= 5,058 10⁵ расп./(мин. мкг) - удельная α-активность ²⁴⁰Рu.

²⁴¹Am образуется из ²⁴¹Рu, распадающегося с периодом 14,4 года. Если после очистки от ²⁴¹Аm прошло более двух дней, требуется учитывать его растущий вклад в пик 5,50+5,46 МэВ.

Случайная погрешность определения ²³⁸Рu может составлять около 2% и меньше при его содержании 0,01% в плутонии. Отношение ²³⁸Pu/²³⁹Pu определяют с погрешностью 2÷5%, что вполне приемлемо для целей контроля образцов плутония и большинства других применений.

Наиболее часто для спектрометрии α-частиц используют поверхностно-барьерные Si(Аu)-детекторы, которые имеют тонкое входное окно (толщиной несколько микрометров) и работают без охлаждения. Площадь чувствительной поверхности Si(Au)-детекторов может достигать 10÷15 см². Однако разрешающая способность больших детекторов обычно хуже, чем малых. Это объясняется увеличением емкости и поверхностных токов утечки. Высокая стабильность полупроводниковых спектрометров позволяет проводить длительные измерения со слабыми источниками. Другое их достоинство - большой (по сравнению с другими спектрометрами) телесный угол, в котором регистрируются вылетающие из источника α-частицы.

В настоящее время серийно производятся пассивные ионно-имплантированные планарные кремниевые (PIPS) детекторы α-излучения. Их активная площадь составляет от 300 до 1200 мм², а энергетическое разрешение – от 17 до 37 кэВ соответственно. С помощью кремниевого спектрометра практически невозможно разделить α-частицы, энергии которых отличаются менее, чем на 50 кэВ.

Ширина пиков в измеренном α-спектре зависит не только от разрешающей способности спектрометра, но и от некоторых искажающих факторов:

1. α-частицы теряют часть энергии внутри источника и в покрывающей его пленке. Для α-частиц с энергией 6 МэВ потери составляют около 0,2 кэВ/(мкг/см²). Из-за этих потерь уменьшается энергия вылетающих из источника α-частиц и увеличивается их разброс по энергии, пики уширяются и сдвигаются в сторону низких энергий, у них появляются длинные «хвосты». Чтобы уширение пиков не превосходило 10 кэВ, слой вещества не должен быть больше 5÷10 мкг/см². Материалом для подложек служит нержавеющая сталь или стекло.

2. α-частицы могут терять энергию в результате взаимодействий с молекулами воздуха в пространстве между источником и детектором. Поэтому источник и детектор помещают в вакуумную камеру. Чтобы уширение и смещение пиков не превосходило 10 кэВ, давление в камере не должно превышать 10 мм.рт.ст. В лучших современных спектрометрах разрежение достигает 10^-4 мм.рт.ст., а для предотвращения загрязнения детектора, вызываемого ядрами отдачи, вылетающими из источника, применяют обратное напряжение, подаваемое на корпус детектора.

3. α-частицы могут терять энергию во входном окне («мертвом» слое) детектора. Из-за разных углов падения α-частиц, их длины пробега во входном окне различны, что обусловливает разные потери энергии. Это ведет к уширению пиков и росту их «хвостов». Чтобы уравнять пробеги, либо удаляют образец от детектора, либо используют диафрагму с коллимирующим отверстием. Применяемые винтовые устройства позволяют изменять расстояние детектор-источник без нарушения вакуума в камере.

Искажение формы линий усложняет математическую обработку α-спектров. В таких случаях нужно использовать специальные вычислительные программы, в которых пики аппроксимируются асимметричными гауссианами.