4. Критический диаметр цилиндрической стенки

Тепловой изоляцией называется всякое покрытие горячей поверхности, которое способствует снижению потерь теплоты в окружающую среду. Для тепловой изоляции могут быть использованы любые материалы с низким коэффициентом теплопроводности – асбест, пробка, слюда, шлаковая или стеклянная вата, шерсть, опилки и т.д.

Запишем выражение для определения линейного термического сопротивления теплопередачи цилиндрической стенки:

.

Анализ этого выражения показывает, что тепловые потери трубопроводов зависят от наружного диаметра трубопровода. Причем в зависимости от материала, применяемого для изоляции трубы, тепловые потери при изменении диаметра теплоизоляционного слоя могут либо увеличиваться, либо уменьшаться.

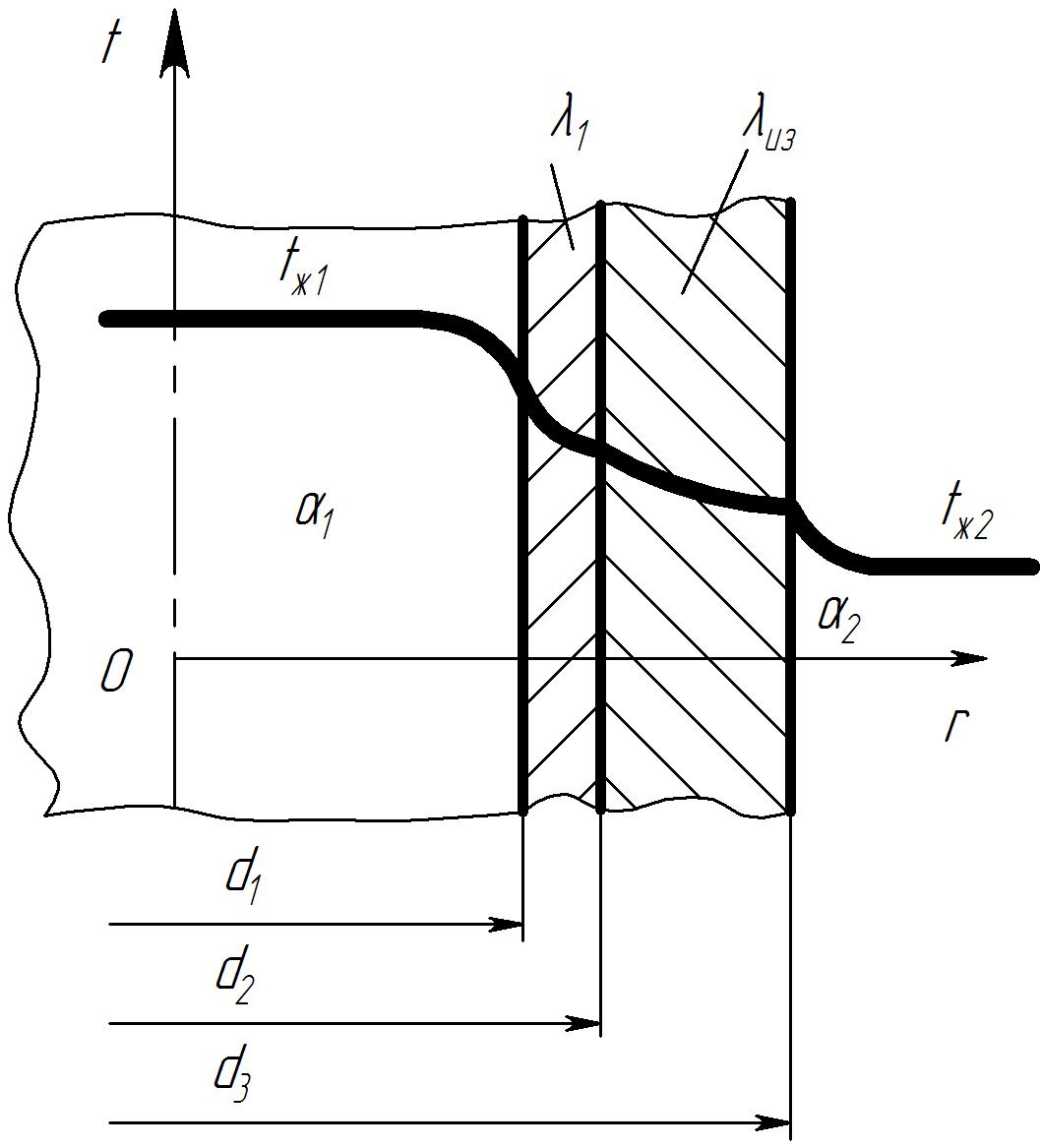
Рассмотрим цилиндрическую трубу покрытую однослойной изоляцией. Установим как при постоянных 1, 2, d1, d2, 1, 2, t1 и t2 будет изменяться полное термическое сопротивление при изменении толщины изоляции. Запишем выражение для определения общего термического сопротивления теплопередачи двухслойной цилиндрической стенки:

.

При увеличении внешнего диаметра изоляции d₃ увеличивается сопротивление слоя изоляции , но одновременно уменьшается сопротивление теплоотдачи на наружной поверхности изоляции .

Чтобы выяснить, как будет изменяться R_l при изменении толщины изоляционного слоя (d₃), исследуем R_l как функцию d₃. Беря первую производную от правой части уравнения по d₃ и приравнивая ее нулю, получаем:

.  .

Исследовав кривую R_l = f(d₃) любым из известных способов на максимум и минимум, увидим, что в экстремальной точке имеет место минимум. Таким образом, при найденном значении d₃ термическое сопротивление теплопередачи будет минимальным, а тепловой поток будет иметь максимальное значение.

Значение внешнего диаметра трубы, соответствующего минимальному полному термическому сопротивлению теплопередачи, называется критическим диаметром и обозначается d_кр. Рассчитывается он по формуле:

.

Из этого уравнения следует, что критический диаметр будет тем меньше, чем меньше коэффициент теплопроводности изоляции и чем больше коэффициент теплоотдачи от наружной поверхности изоляции к окружающей среде.

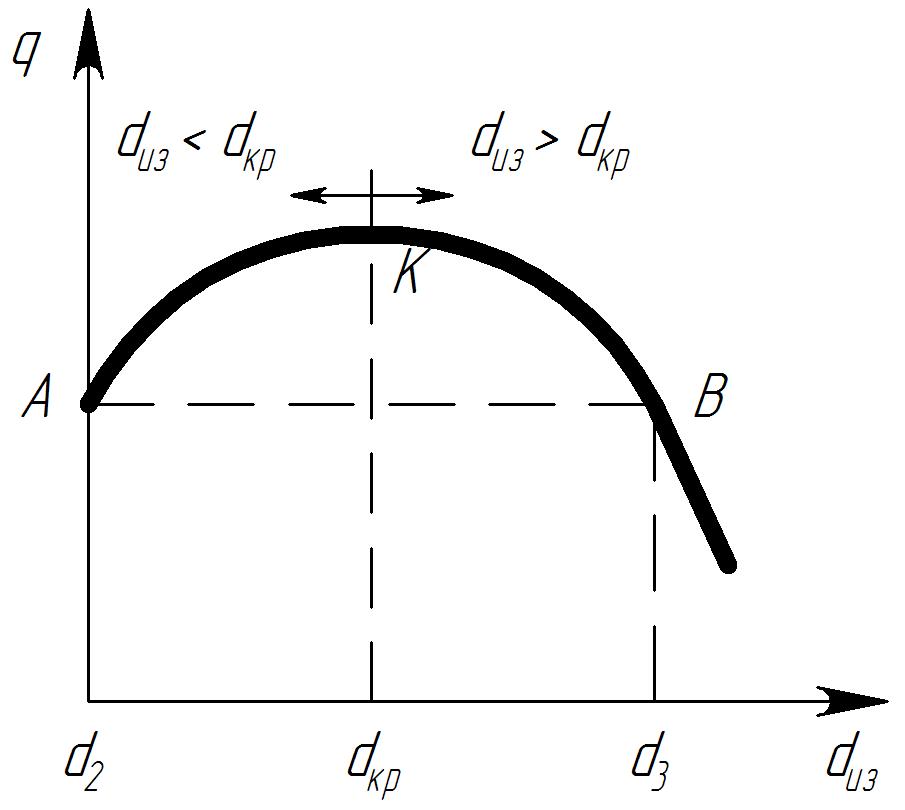
Рассмотрим зависимость линейной плотности теплового потока от диаметра изоляции.

Из графика видно, что если наружный диаметр изоляции dиз увеличивается, но остается меньше dкр, то тепловые потери возрастают и будут больше теплопотерь голого трубопровода (кривая АК). При равенстве dиз = dкр получаются максимальные теплопотери в окружающую среду (точка К). При дальнейшем увеличении наружного диаметра изоляции dиз > dкр теплопотери будут меньше, чем при dиз = dкр.

Только при d_из = d₃ тепловые потери вновь станут такими же, как и для неизолированного трубопровода.

Значит для эффективной работы изоляции необходимо, чтобы критический диаметр был меньше внешнего диаметра оголенного трубопровода, то есть d_кр  d₂. Следовательно,

 .