- •1. Передача теплоты через плоскую стенку и граничных
- •2. Передача теплоты через многослойную плоскую стенку и
- •3. Передача теплоты через плоскую однослойную и многослойную стенки и граничных условиях III рода
- •1. Передача теплоты через цилиндрическую стенку
- •2. Передача теплоты через многослойную цилиндрическую стенку
- •3. Передача теплоты через однослойную и многослойную
- •4. Критический диаметр цилиндрической стенки
- •5. Передача теплоты через ребристую стенку
- •6. Теплопроводность при наличии внутренних источников теплоты
1. Передача теплоты через цилиндрическую стенку
и граничных условиях I рода
|
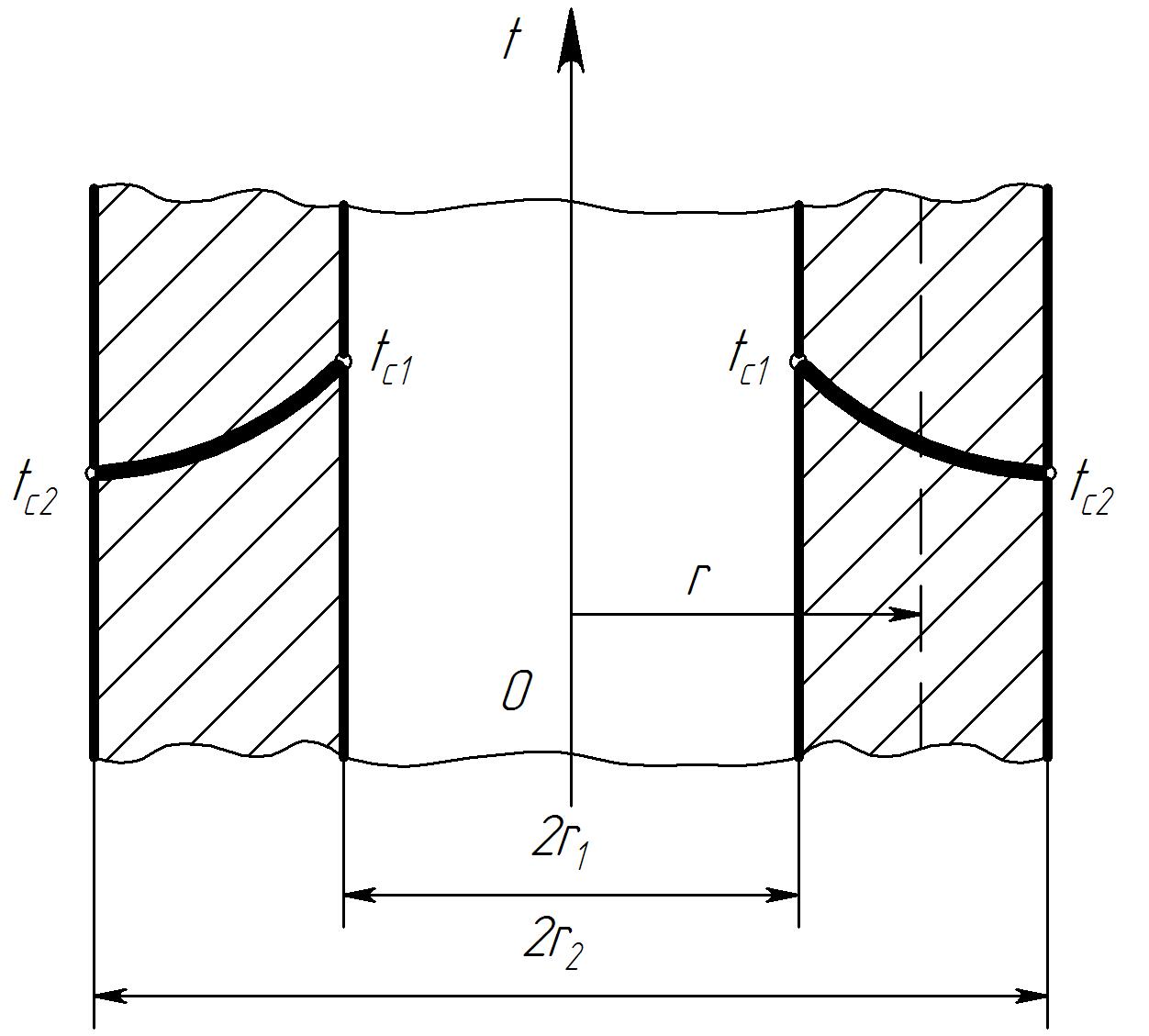
Подвод теплоносителя к потребителю обычно осуществляется по трубам, а сами потребители часто имеют цилиндрический корпус. В связи с этим возникает необходимость расчета тепловых потоков через цилиндрическую оболочку. Рассмотрим стационарный процесс теплопроводности в цилиндрической стенке (трубе) с внутренним диаметром d1 = 2r1 и наружным диаметром d2 = 2r2. На поверхности стенки заданы |
постоянные температуры tc1 и tc2. В заданном интервале температур =const. Необходимо найти распределение температур в цилиндрической стенке и тепловой поток через нее.
В рассматриваемом случае дифференциальное уравнение теплопроводности удобно записать в цилиндрической системе координат:
![]() .
.
При этом ось Oz совмещена с осью трубы.
При заданных условиях температура изменяется только в радиальном направлении и температурное поле будет одномерным, поэтому:
![]() и
и
![]() .
.
Кроме того, так как температуры на наружной и внутренней поверхностях трубы неизменны, изотермические поверхности являются цилиндрическими. Тогда температура не должна изменяться вдоль , то есть:
![]() и
и
![]() .
.
Следовательно, дифференциальное уравнение теплопроводности примет вид:
![]() .
.
Граничные условия задаются следующим образом:
t = tc1 при r = r1;
t = tc2 при r = r2.
Для решения дифференциального уравнения введем новую переменную:
![]()
![]() .
.
Тогда дифференциальное уравнение примет вид:
![]() .
.
Интегрируя, получаем:
![]()
![]() .
.
Потенцируя и переходя к первоначальным переменным, получаем:
![]()
![]() .
.
После интегрирования находим:
![]() .
.
Подставим в полученное выражение граничные условия:
|
|
 ;
;  .
.
Тогда температурное поле будет равно:
 ,
,
 или
или
 .
.
Полученное выражение представляет собой уравнение логарифмической кривой. Криволинейное распределение температуры в цилиндрической стенке объясняется следующим. Для плоской стенки плотность теплового потока q остается одинаковой для всех изотермических поверхностей. Для цилиндрической стенки q через любую изотермическую поверхность зависит от радиуса.
Для нахождения количества теплоты, проходящего через цилиндрическую поверхность площадью F в единицу времени, воспользуемся законом Фурье:
![]() .
.
Очевидно,
 ;
; ![]() .
.
Тогда Q равно:
 .
.
Из полученного выражения видно, что так же, как и для плоской стенки, тепловой поток через цилиндрическую оболочку прямо пропорционален разности температур поверхностей стенки.
Тепловой поток может быть отнесен либо к единице длины трубы, либо к единице внутренней или внешней поверхности. При этом расчетные формулы для плотности теплового потока, принимают вид:
 -
тепловой
поток через единицу внутренней
поверхности;
-
тепловой
поток через единицу внутренней
поверхности;
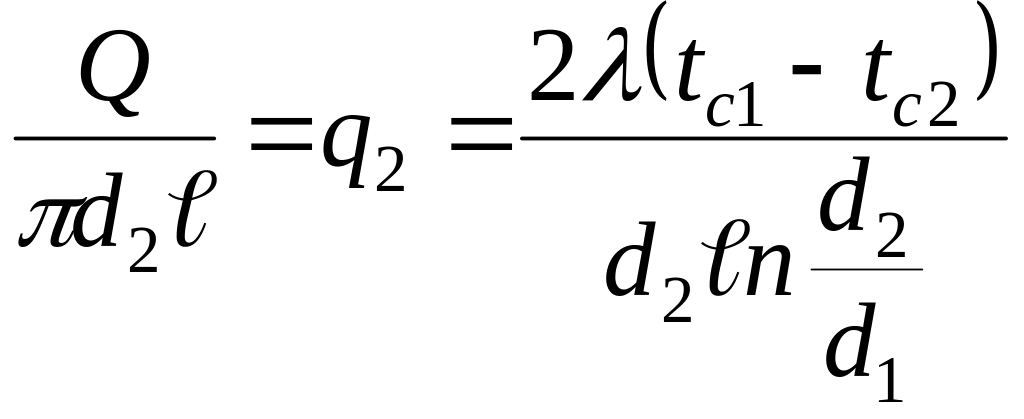 -
тепловой
поток через единицу наружной поверхности;
-
тепловой
поток через единицу наружной поверхности;
 -
поток теплоты, проходящий через единицу
длины трубы.
-
поток теплоты, проходящий через единицу
длины трубы.
ql также называется линейной плотностью теплового потока (Вт/м).
Как видно из первых двух уравнений плотности теплового потока q1 и q2 (отнесенные к внутренней и внешней поверхности) при передаче теплоты через трубы неодинаковы, причем всегда q1 > q2.
Связь между величинами q1, q2 и ql следующая:
![]() .
.