2.1. Кодирование

Идея кодирования возникла давно и преследовала в основном быстроту и секретность передачи информации. В современных условиях кодирование используется и для создания условий, обеспечивающих надежную и экономичную передачу сообщений по каналам связи.

Под кодированием понимают процедуру сопоставления дискретному сообщению вида: ai (i=1, 2, 3, …,к) определенной последовательности кодовых символов, выбираемых из конечного множества различных элементарных кодовых символов: bi (i=1, 2, 3, …,m).

В кодировании используются различные системы счисления.

Из всех систем счисления практическое назначение имеют: двоичная (R=2), троичная (R=3), четверичная (R=4), восьмеричная (R=8) и десятичная (R=10). Кроме этих систем, человек издавна пользуется двенадцатиричной системой, отсчитывая время, и шестидесятиричной для отсчета углов. Во всех системах используется различное количество цифр. Например: в двоичной используется две цифры: 0 и 1 (011001). Представление машинных кодов производится в шестнадцатеричной системе счисления, где для кодирования информации используется сочетание цифр (0, 1, 2, …9) и букв (A, B, C, D, E, F).

В кодировании используются различные типы кодов: равномерный, неравномерный, избыточный, безизбыточный, помехоустойчивый, оптимальный.

Повышение коэффициента использования канала достигается за счет создания оптимального кода, т.е. вероятность встречаемости элементов одинакова.

Базовыми являются коды Морзе и Шеннона - Фанно.

Код Морзе: наиболее часто встречающимся знакам присваиваются наименее короткие и наоборот.

1.3 Что такое верность передачи?

Любые сигналы телемеханических систем состоят из той или иной совокупности импульсов, передаваемых по каналу связи. Правильное опознание сигналов на приемной стороне означает верный (достоверный) прием переданного сообщения. Это возможно в том случае, если принимаемые импульсы искажены не настолько, чтобы приемное устройство не различило импульсных признаков сигналов логических 1 и 0. При передаче кодовой комбинации достоверный прием возможен, если число ошибок в опознании сигналов 1 и 0 не превысило корректирующих возможностей кода.

1.4 В каком случае энтропия дискретного ансамбля равна нулю?

Максимум энтропии имеет место при p=1/2, т. е. когда ситуация является наиболее неопределенной. При р = 1 или р = 0, что соответствует передаче одного из сообщений а₁, или а₂, неопределенности отсутствуют. В этих случаях энтропия Н(а) равна нулю.

1.5 Как определить энтропию нескольких статистически независимых источников информации?

Энтропия объединения нескольких статистически независимых источников информации равна сумме энтропии исходных источников.

Не теряя общности, ограничимся рассмотрением объединения, включающего два источника информации u и υ. Под объединением двух источников u и υ понимают обобщенный источник информации (u,υ), характеризующийся вероятностями p(uiυi) всех возможных комбинаций состояний ui, источника u и υi, источника υ. Аналогично трактуется и объединение ансамблей.

В соответствии с определением энтропия объединения

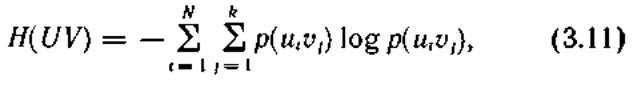
здесь p(uiυi) —вероятности совместной реализации состояний

В случае статистической независимости источников информации u и υ запишем

тогда

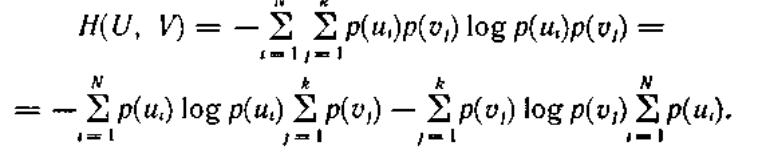
Учитывая, что

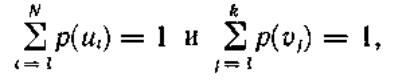
получим

Соответственно для энтропии объединения нескольких независимых источников u, υ, z имеем

В дальнейшем для придания общности получаемым результатам о неопределенности выбора будем говорить в основном применительно к математическим моделям источников информации в виде ансамблей.

1.6 Что такое частное количество информации?

Поскольку получение информации мы связываем с уменьшением неопределенности, естественно определить частное количество информации , получаемое при приеме элемента сообщения относительно некоторого реализованного источником элемента сообщения как разность частных неопределенностей, имевшихся у адресата до и после получения элемента сообщения (априорной и апостериорной):

Задание 2. Написать формулы для расчета следующих величин:

2.1 Меры неопределенности выбора состояния источника информации по

Р. Хартли

К. Шеннону

где С — произвольное положительное число.

2.2 Условной энтропии ансамбля V по отношению к ансамблю U

2.3 Количества информации при неполной достоверности передачи

а) от дискретного источника

б) от непрерывного источника.

Задание 3. Решить задачу

Имеются 2 урны, содержащие по 10 шаров:

1 урна - 5 белых, 3 черных, 2 красных.

2 урна - 3 белых, 3 черных, 4 красных.

Из каждой урны вытаскивают по одному шару.

Результат какого из этих двух событий следует считать более определенным?

Решение:

Урна-1

Цвет вынутого шара	белый	черный	красный
Вероятность	1\2	1\3,3	1\5
Энтропия (неопределенность)	-1\2 log 1\2	-1\3,3 log 1\3,3	-1\5 log 1\5

Неопределенность данного опыта, или энтропия равна:

Н (α)= -1\2 log 1\2 - 1\3,3 log 1\3,3 - 1\5 log 1\5 = 1/2 + 1/3,3 + 1/5 = 3/10,3

Н (α)= -1\2 log 1\2 - 1\4 log 1\4 - 1\4 log 1\4 = 1\2 +1\2 +1\2 = 3\2 бита

Урна-2

Цвет вынутого шара	белый	черный	красный
Вероятность	1\3	1\3	1\2,5
Энтропия (неопределенность)	-1\3,3 log 1\3,3	-1\3,3 log 1\3,3	-1\2,5 log 1\2,5

Н (α)= -1\3,3 log 1\3,3 - 1\3,3 log 1\3,3 - 1\2,5 log 1\2,5 = 1/3,3 + 1/3,3 + 1/2,5 = 3/

Задача №1/2. Имеются 2 урны. Первая содержит 20 шаров – 10 белых, 5 черных и 5 красных; вторая содержит 16 шаров: 4 белых, 4 черных и 8 красных во второй. Из каждой урны вытаскивают по одному шару. Исход какого из этих двух опытов следует считать более неопределенным? 16

Решение: Первый опыт связан с первой корзиной:

Цвет вынутого шара	белый	черный	красный
Вероятность	1\2	1\4	1\4
Энтропия (неопределенность)	-1\2 log 1\2	-1\4 log 1\4	-1\4 log 1\4

Неопределенность данного опыта, или энтропия равна: Н (α)= -1\2 log 1\2 - 1\4 log 1\4 - 1\4 log 1\4 = 1\2 +1\2 +1\2 = 3\2 бита Второй опыт связан со второй корзиной:

Цвет вынутого шара	белый	черный	красный
Вероятность	1\4	1\4	1\2
Энтропия (неопределенность)	-1\4 log 1\4	-1\4 log 1\4	-1\2 log 1\2

Неопределенность данного опыта, или энтропия равна: Н (β)= -1\2 log 1\2 - 1\4 log 1\4 - 1\4 log 1\4 = 1\2 +1\2 +1\2 = 3\2 бита Ответ: опыты одинаково неопределенны.