Задание 5 Разбиение на интервалы в Excel

Рассмотрим задачу из образца Задания 1. Представим выборку в виде интервального распределения частот тремя способами.

Способ 1. Представление признака в шкале «низкий уровень – средний уровень – высокий уровень» (или подобной). В данном случае будем считать

«низкий уровень» - [0; 7] баллов,

«средний уровень» - [8; 15] баллов,

«высокий уровень» - [16; 20] баллов.

Для этого:

1. Занести показатели в таблицу (в строку или столбец),

2. подсчитать частоты (количество попаданий значений выборки в данный интервал) используя или функцию частота, или функцию счетесли, или сводные таблицы с фильтрами,

3. оформить результат (в данном случае использована функция счетесли)

Способ 2. Используя параметры распределения (выборочное среднее, дисперсия, стандартное отклонение), можно разбить на интервалы по стандартному отклонению или по половине стандартного отклонения:

Для этого:

1. Занести показатели в таблицу (в строку или столбец),

2. подсчитать числовые характеристики выборки (см. Задание 3)

3. подсчитать границы интервалов

4. подсчитать частоты (количество попаданий значений выборки в данный интервал) используя или функцию частота, или функцию счетесли, или сводные таблицы с фильтрами. В данном случае использована функция ЧАСТОТА

5. оформить результат

Способ 3. Применение формулы Стерджеса. Формула Стерджеса предлагает разбить признак на k интервалов, где с шагом (max - наибольшее возможное значение признака, min - наименьшее возможное значение признака). Для этого:

Для этого:

6. Занести показатели в таблицу (в строку или столбец),

7. подсчитать необходимые характеристики

8. подсчитать границы интервалов (аналогично предыдущим способам) и оформить результат

Самостоятельно

Построить разбиение на интервалы всеми способами признака «Коммуникативная компетентность», полученного по опросу в группе педагогов, проходящих курсы повышения квалификации.

10

15

12

12

9

8

12

14

14

8

11

11

14

13

13

12

15

14

10

11

Считать при этом:

«низкий уровень» - [0; 6] баллов,

«средний уровень» - [7; 12] баллов,

«высокий уровень» - [13; 16] баллов.

Задание 6 Полигон и гистограмма в Excel

Образец

Рассмотрим задачу из образца Задания 1. Пусть построено статистическое распределение выборки. Построим полигон частот. Для этого:

1. выделить интервал, содержащий частоты,

2. во вкладке Вставка в группе Диаграммы нажать на кнопку Графики и выбрать График с маркерами

3. настроить появившуюся диаграмму, используя контекстное меню и вкладки Макет и Конструктор

Результат:

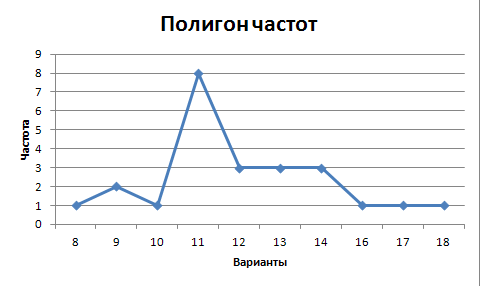
Построим гистограмму. Для этого:

1. возьмем границы интервалов из Задания 5 (способ 3)

2. во вкладке Данные в группе Анализ нажать на кнопку Анализ данных

3. в окне Анализ данных в списке инструментов выбрать Гистограмма и нажать OK.

4. в появившемся диалоговом окне Гистограмма указать необходимые параметры

4. настроить появившуюся гистрограмму, используя контекстное меню и вкладки Макет и Конструктор

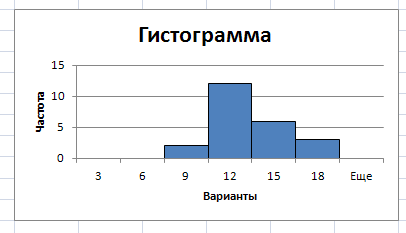
Самостоятельно

Для задачи из самостоятельной части Задания 2 подсчитать построить полигоны частот и относительных частот, гистограммы частот и относительных частот для каждой группы отдельно.