6. Продольно-поперечный изгиб и устойчивость стержней

1. Продольно-поперечный изгиб

Изгиб прямого стержня называется продольно-поперечным, если в поперечных сечениях возникают изгибающие моменты не только от поперечных, но и от продольных нагрузок (рис. 6.1). Изгибающие моменты при расчете на продольно-

Рис. 6.1

поперечный изгиб вычисляют с учетом прогибов оси стержня. Полный прогиб стержня V_п. в этом случае можно представить как прогиб V, возникающий от действия только одних поперечных нагрузок, и дополнительного прогиба V_п - V, вызванного действием продольной нагрузки. Наибольший интерес представляет случай, когда продольные силы являются сжимающими, так как совершенно очевидно, что полный прогиб стержня V_п больше прогиба V от действия одной только поперечной нагрузки.

Используя уравнения равновесия для элемента прямого стержня в неподвижной системе координат и присоединяя к ним геометрические соотношения, формулы закона Гука, получаем математическую модель поставленной задачи, т.е. дифференциальное уравнение, описывающее продольно-поперечный изгиб прямого стержня с произвольным характером изменения жесткости :

. (6.1)

При отсутствии продольных погонных нагрузок ( ) величина остается величиной постоянной по всей длине стержня. Учитывая это и рассматривая стержень с постоянной жесткостью , записываем уравнение (6.1) в виде

, (6.2)

где введены следующие обозначения:

и .

Используя метод Коши, решение дифференциального уравнения (6.2) можно представить в виде суммы общего решения соответствующего однородного дифференциального уравнения без правой части и частного решения с правой частью:

, (6.3)

где V₁(z), V₂(z),V₃(z) и V₄(z) - фундаментальные функции; A, B, C, D - постоянные интегрирования, определяемые из граничных условий; Ф(z) – функция, зависящая от нагрузки (нагрузочная функция).

Если в качестве фундаментальных функций выбрать функции с единичной матрицей при значении аргумента, равном нулю, то постоянные интегрирования A, B, C и D приобретают определенный геометрический и физический смысл:

A=V(0) – линейное перемещение в начале координат; −

угловое перемещение в начале координат;

– изгибающий момент в начале координат;

– поперечная сила в начале координат;

а нагрузочная характеристика получит простой вид

. (6.4)

Фундаментальные функции V₁( z ), V₂( z ),V₃( z ) и V₄( z ) можно образовать из линейной комбинации независимых уравнений, удовлетворив требованиям:

,	,	,	,
,	,	,	,
,	,	,	,
,	,	,	.

В результате получим

, , , . (6.5)

Теперь общее решение дифференциального уравнения (6.2) с использованием фундаментальных функций (6.5) можно записать в следующем виде:

, (6.6)

где . (6.7)

Решение уравнения (6.2) в виде (6.7) содержит четыре постоянные интегрирования: A, B, C и D, которые определяются из граничных условий, заключающихся в том, что известна дополнительная информация о перемещениях и силах или их комбинациях в концевых сечениях стержня. Различают два основных вида граничных условий:

а) силовые граничные условия, когда в концевом сечении заранее известны интегральные характеристики и ;

б) геометрические (кинематические) граничные условия, когда имеется информация о линейных и угловых перемещениях концевого стержня.

Рис. 6.2

Особую группу представляют граничные условия смешанного типа, содержащие информацию в виде зависимости между усилиями и перемещениями концевого сечения. Рассмотрим одно из этих граничных условий, которое будет встречаться при расчете стержня на продольно-поперечный изгиб. Под действием сжимающей силы Р, не изменяющей своего направления,

стержень займет новое положение (рис. 6.2), и на свободном конце возникнет поперечная сила Q.

Составим уравнение равновесия, спроектировав силы на направление Q: , но , следовательно, получим или .

Остальные граничные условия аналогичны известным для любых способов закрепления концов стержня.

Вычисление нагрузочной функции

Рис. 6.3

Допустим в точках а₁, а₂, а₃, ..., а_n (рис. 6.3 ) имеются какие-то особенности, при переходе через эти точки получим приращение функции .

Приращение функции характеризует изменение внешней нагрузки в данной точке.

а) Пусть в точке «α» начинает действовать поперечная погонная нагрузка постоянной

интенсивности q (рис. 6.4).

Рис. 6.4

тогда приращение функции

(6.8)

Рис. 6.5

б) Если действие поперечной погонной нагрузки постоянной интенсивности q (рис. 6.5) кончается, то приращение функции в точке «α» будет иметь вид (6.8), взятый с обратным знаком:

(6.9)

Рис. 6.6

в) В точке «α» приложена сосредоточенная сила Р. Ее можно представить как погонную нагрузку бесконечно большой интенсивности q, действующей на бесконечно малом отрезке [α, α+ ] таким образом, что при 0 величина q P (рис. 6.6). Тогда

Вычислим приращение функции

на бесконечно малом отрезке [αα+ ]:

,

воспользовавшись теоремой о среднем значении, получим

.

Учитывая, что - длина интервала, - промежуточная точка этого интервала и при 0 α, находим

. (6.10)

Рис. 6.7

г) В точке «α» приложена пара сил L (рис. 6.7). Эту пару сил L можно представить в виде произведения сосредоточенной силы Р на плечо , причем при 0 Р^. L, тогда получаем (6.11)

Таким образом, для стержня постоянной жесткости при любой комбинации внешних нагрузок можно определить нагрузочную функцию по приведенным выражениям

(6.8) – (6.11).

Необходимо иметь в виду, что момент инерции J во всех выражениях следует брать относительно той из главных осей инерции сечения, которая перпендикулярна к плоскости действия поперечной нагрузки.

Примеры решения задач

Задача 1

Двутавровая балка №10 (ГОСТ 8239-72) Нагружена поперечной погонной нагрузкой постоянной интенсивности q=5 кН·м и сжимающей силой P=80 кН (рис.6.8).

Построить графики функций , , , , а также вычислить максимальные нормальные напряжения . Площадь поперечного сечения двутавра F=12 см², осевой момент инерции J_x=198 см². Длина балки l=2 м. Модуль упругости материала балки E=2^.10⁵ МПа.

И спользуя формулы (6.8) и (6.9) нагрузочной функции при действии погонной нагрузки постоянной интенсивности q, запишем уравнение линейных перемещений и его производные, учитывая, что постоянные А и С (линейное перемещение и изгибающий момент в начале координат) равны нулю:

;

Рис. 6.8

.

Постоянные интегрирования B и D определим из

граничных условий при z=l на правом конце стержня. Эти условия позволяют получить два уравнения, из которых и определяем постоянные B и D:

.

,

.

Используя B и D, вычисляем , , , в характерных точках по длине стержня. Результаты вычислений сведем в табл. 6.1.Графики функций , , , показаны на рис. 6.8.

Таблица 6.1

Абсцисса сечения м	0	0,375l	l/2	l
	0	0,75l	1	2
, см	А=0	– 0,12	– 0,11	0
.10 -3, рад	– В=2	0,9	– 0,2	–1,7
, кН.м	С=0	–1,55	–1,35	0
, кН	–EID=–3,9	0	1,3	1,3

Так как поперечная сила меняет свой знак, то функция имеет экстремум. Исследуем функцию на экстремум:

.

Из этого уравнения , тогда 0,306 и 0,375l =0,75 м.

Момент в сечении 0,75 м имеет максимальное значение

= –1,55 кН·м.

Аналогично исследуется на экстремум функция , так как =0. Функция меняет свой знак при 0,9 м. Экстремальное значение =0,13 м.

Максимальные нормальные напряжения определяются по формуле

.

Задача 2

Определить максимальные нормальные напряжения в поперечном сечении заделанной в стену балки от действия пары сил L=5 кН·м и осевой сжимающей силы

P=20 кН, приложенных на левом конце балки (рис. 6.9). Сечение балки прямоугольное со сторонами 6,4 см и 12 см. Длина балки l=3 м. При расчетах учесть собственный вес балки ( =78 кН/м³). Модуль упругости материала Е=2,1^.10⁵ МПа. Построить графики , , , .

Запишем уравнение перемещений и его производные в сечении z, используя формулы (6.8) нагрузочной функции от q и формулу (6.11) нагрузочной функции от L:

;

;

Рис. 6.9

;

.

Установим граничные условия. На свободном конце имеем одно силовое, уже использованное , и одно комбинированное граничное условие . В защемленном сечении балки имеем два кинематических граничных условия: V(l)=0 и . Используя эти условия, получим три уравнения:

;

;

.

Решив систему уравнений, получим

,

,

.

Подставив значения найденных постоянных в уравнениях V(z), , и , вычислим значения в характерных точках оси балки и результаты вычисления сведем в табл.6.2.

Таблица 6.2

Абсцисса сечения	V(z), см	−	, кН м	, кН
0	0,9	6,5.10-3	–5,0	– 0,13
0,07l	0,77	3,7.10-3	–5,53	0
l	0	0	–2,5	1,8

Так как поперечная сила меняет свой знак, то функция имеет экстремум. Исследуем функцию на экстремум:

.

Решив уравнение, найдем = 0,07l = 0,21 м. Изгибающий момент в сечении принимает максимальное значение M_X =5,53 кН·м.

Вычислим максимальные нормальные напряжения

 МПа.

Задача 3

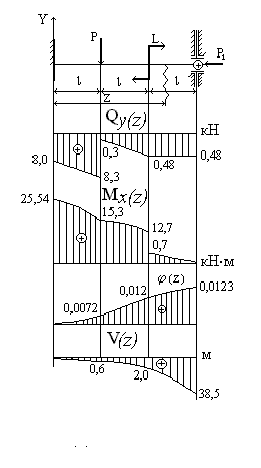
Двутавровая балка № 20а (ГОСТ 8239-72) нагружена, как показано на рис. 6.10.

P=8 кН, L=Pl=12 кН^.м, Р₁=40 кН, l=1,5 м, E=2^.10⁵ МПа, J_x=2030^.10^-8 м⁴. Построить графики , , , .

^{Запишем уравнение перемещений и его производные:}

,

;

.

Установим граничные условия:

;

Рис. 6.10

.

Решив систему уравнений, получим

и ,

где .

С учетом этих коэффициентов запишем уравнения для определения , , , :

;

;

;

Результаты вычислений значений , , , в характерных сечениях стержня сведены в табл. 6.3.

Таблица 6.3.

Абсцисса	V(z), см	, рад	, кН м	, кН
0	А=0	В=0	=25,54	=– 8,0
l	–0,6	0,0072	13,3	Z < l Z > l – 8,3 –0,3
2l	–2,0	–0,120	Z < 2l Z > 2l 12,7 0,7	– 0,480
3l	–38,5	0,0123	0	– 0,485

Графики , , , показаны на рис. 6.10.