3. Деревья решений
Для представления своих возможных действий и для нахождения последовательности правильных решений используется дерево решений.
Рассмотрим пример задачи с вазами. Экспериментатор случайно выбирает вазу из множества ваз, содержащего 700 ваз 1-го типа и 300 ваз 2-го типа. Если перед испытуемым находится ваза 1-го типа и он угадает это, то он получит выигрыш 350 у.е., если не угадает, то его проигрыш составит 50 у.е. Если перед ним ваза 2-го типа и он это угадает, то получит выигрыш 500 у.е., если не угадает, его проигрыш составит 100 у.е. Испытуемый может предпринять одно из следующих действий: d1 – сказать, что ваза 1-го типа; d2 – сказать, что ваза 2-го типа.
Условия задачи можно представить в таблице 1.
Таблица 1.
Тип вазы |
Вероятность выбора вазы данного типа |
Действия и выигрыш |
|
d1 |
d2. |
||
1 |
0.7 |
350 |
-100 |
2 |
0.3 |
-50 |
500 |
Какое действие предпринять человеку?
На основе теории полезности для этого необходимо оценить среднюю (ожидаемую) полезность каждого из действий и выбрать действие с максимальной ожидаемой полезностью. Оценка полезности дает:
U (d1) = 0.7 *350 – 0.3 * 50 = 230 y.e.
U (d2) = 0.3 *500 – 0.7 * 100 = 80 y.e.
Следовательно, разумный человек выберет действие d1, а не действие d2.
Отсюда следует общий рецепт действий для рационального человека: для каждого действия определить ожидаемую полезность и выбрать действие с наибольшей полезностью.
Таблица 1. может быть представлена в виде дерева решений .
Дерево решений удобно использовать для представления своих возможных действий и для нахождения последовательности правильных решений, ведущих к максимальной ожидаемой полезности.
4. Парадокс Алле
Рассмотрим две лотереи, представленные на рис. 2.
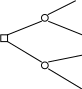
1 млн. 0,1 5 млн.
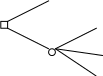А
С
0,1 5 млн. 0,9 0
В 0,89 0,11 1 млн.
1 млн. D
0,01 0,89
0 0
Рис. 2. Парадокс Алле
Обозначим: U ( 5млн )=1; U(1млн ) =U; U (0) = 0.
В левой лотереи есть выбор между действиями А (получить 1 млн.) и В (согласиться на лотерею). В экспериментах подавляющее большинство людей предпочитает А. Откуда следует
U > 0.1*1 + 0.89*U + 0.01*O или U > 10/11
В правой лотерее есть выбор между действиями С и D (две лотереи). Подавляющее большинство людей предпочитает действие С (почти та же вероятность проиграть, но выигрыш больше). Тогда
0.1*1 + 0.9*O > 0.11*U + 0.89*O т.е. U < 10/11.
Совершая такой выбор, люди действуют не в соответствии с функцией полезности. Полученный парадокс носит название парадокса Алле.
Рассмотрим ещё пример. Две лотереи, показанные на рис.3 имеют одинаковые средние цены.
0,5
44
0,6 50
0,4 -20 0,5 0
Рис. 3. Сравнение 2-х лотерей
0.6*50 + 0.4* (-20) = 22
0.5*44 + 0.5 * 0 = 22.
Однако предъявление различным группам лотерей показало, что люди предпочитают правую лотерею, где при той же средней цене риск проигрыша исключен. Эти и другие примеры говорят о нерациональном поведении людей в задачах принятия решений.