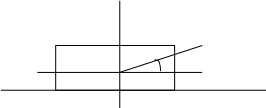
Задача №11. Груз массой m=100 кг равномерно перемещают по поверхности, прилагая силу F под углом a=30⁰ к горизонту. Коэффициент трения равен k=0,3. Найти величину этой силы.

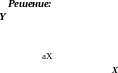
Дано:

m=100 кг

a =30⁰

k

=0,3

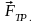
F– ?

Инерциальная система отсчёта - “Земля”. Груз - материальная точка.

Второй закон Ньютона: ускорение, приобретаемое материальной точкой в инерциальной системе отсчёта, прямо пропорционально действующей на точку силе (равнодействующей сил), обратно пропорционально массе точки и по направлению, совпадает с силой:

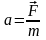
На материальную точку действуют силы:

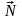- сила реакции опоры; 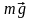- сила тяжести; - сила трения; - сила, действующая на материальную точку под углом a.

Запишем второй закон Ньютона для материальной точки, перемещающейся равномерно по поверхности под действием указанных сил:

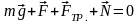
Запишем второй закон Ньютона для материальной точки, перемещающейся равномерно по поверхности под действием указанных сил, в проекции на ось Х:

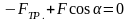(1)

Запишем второй закон Ньютона для материальной точки, перемещающейся равномерно по поверхности под действием указанных сил, в проекции на ось Y:

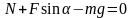(2)

Сила трения скольжения 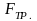пропорциональна силе N нормального давления, с которой одно тело действу­ет на другое:

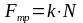, (3)

где 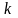- коэффициент трения скольжения, зависящий от свойств соприка­сающихся поверхностей.

Выразим из формулы (2) значение силы нормальной реакции

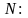
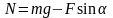(4)

Подставим выражение (4) в формулу (3):

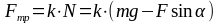(5)

Подставим выражение (5) в формулу (1) и решим полученное уравнение относительно силы F:

.

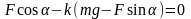
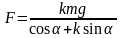Проверим размерность полученного результата:

.

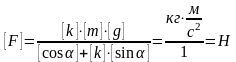Проведём расчёты:

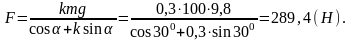
Ответ: величина силы F равна 289,4 Н.

Задача №12. Лодка массой 100 кг стоит неподвижно в стоячей воде. Мальчик массой 40 кг переходит с кормы на нос лодки. На сколько при этом передвинется лодка (S-?), если её длина 2 м? Сопротивлением воды пренебречь.

Д ано:

m_Л =100 кг

m_М =40 кг

l = 2 м

S

_Л -?

Импульсом материальной точки называется векторная величина, равная произведению массы точки на скорость её движения

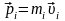
Импульс системы, состоящей из n материальных точек, равен сумме импульсов всех точек системы

, .

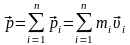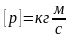В случае отсутствия внешних сил (рассматриваем замкнутую систему)

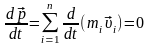, т.е .

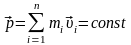
Последнее выражение - закон сохранения импульса: им­пульс замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Пусть система “мальчик-лодка” - замкнутая. Применим закон сохранения импульса для рассматриваемой системы.

,

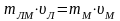где .

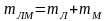Таким образом, .

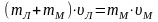По определению, . Значит, , .

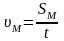Найдём расстояние, которое прошёл мальчик: .

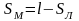Таким образом, , .

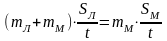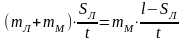Выполним преобразования и выразим расстояние, на которое передвинется лодка:

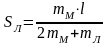
Проверим размерность:

=

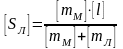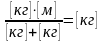
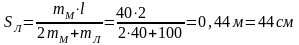
Ответ: лодка передвинется на 44 см.

Задача №13. Определить массу азота, содержащегося в баллоне объёмом 2,0×10^-2 м³ , если суммарная кинетическая энергия поступательного движения молекул и средняя квадратичная скорость одной молекулы азота соответственно равны: 5,0×10³ Дж и 2,0×10³ м/с. Вычислить давление газа.

Решение:

Cредняя квадратичная скорость 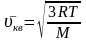(1).

Средняя кинетическая энергия поступательного движения:

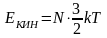, (2)

где N - число молекул, i = 3 - число степеней свободы.

Д ано:

V = 2,0×10^-2 м³

Е_кин=5,0×10³ Дж

u_ср.= 2,0×10³ м/с

р - ?

m - ?

Числом степеней свободы (i) – называется число независимых координат, которые необходимо знать для определения положения материальной точки или системы материальных точек в пространстве.

Для нахождения давления воспользуемся основным уравнением молекулярно-кинетической теории:

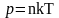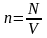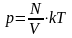, поскольку концентрация молекул , то (3)

Из уравнения (2) выразим температуру Т :

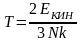
Подставим в уравнение (3): .

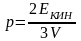Проверим размерность:

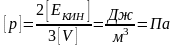
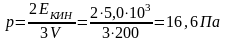
Масса газа 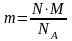(4), где . Между молярной массой М и относительной молекулярной массой M_r, существует следующая связь 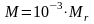кг/моль

Выразим из формулы (3) выразим количество молекул N: 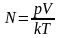(5).

Подставим (5) в (4): 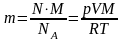(6). Из уравнения (1) выразим температуру: 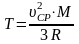. Таким образом,

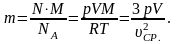
Проверим размерность: .

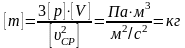Ответ: масса азота равна 0,0025 кг, давление азота равно 16,6 Па.

Задача №14. На поверхности Земли барометр показывает 1,01×10⁵ Па. Каково будет показание барометра при подъёме его на телевизионную башню Московского телецентра в Останкино высотой 533 м? Температура атмосферного воздуха равна 280 К. Какова концентрация молекул на этой высоте?

Д

Решение:

Учёт поля тяготения приводит к сложному распределению молекул, возникающих в результате сочетания двух факторов: теплового движения молекул и силы тяжести. При этом получается следующая формула зависимости концентрации молекул земной атмосферы от высоты:

,

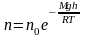ано:

р₀=1,01×10⁵ Па

h=533 м

Т=280 К

р₁ - ?

n - ?

где M – молярная масса, входящего в состав атмосферы воздуха, R – универсальная газовая постоянная, T – абсолютная температура газа, g – ускорение свободного падения.

Больцман показал, что распределение молекул по высоте, описываемое данной формулой, является универсальным статистическим законом распределения и справедливо для любых частиц, совершающих тепловое движение в любом потенциальном силовом полю. Если на оси ординат отложить вероятность нахождения молекулы в заданном интервале высот, на оси абсцисс всевозможные значения высоты, на которой может оказаться молекула, то получим кривую, называемую экспонентой и графически изображающую статистический закон распределения молекул по высоте. Из графика видно, что наибольшая вероятность нахождения молекулы соответствует поверхности Земли, а с увеличением высоты эта вероятность уменьшается.

Известно, что атмосферное давление убывает с высотой, поэтому можно получить барометрическую формулу:

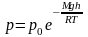
Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределения Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.

Воспользуемся барометрической формулой для расчёта давления р₁:

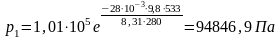
Для нахождения концентрации молекул воспользуемся основным уравнением молекулярно-кинетической теории:

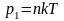
Таким образом, концентрацию молекул найдём по формуле:

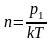
Проверим размерность: .

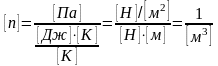Следовательно,

Ответ: показание барометра будет , концентрация молекул на указанной высоте равна

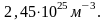
Задача №15. Какова будет средняя кинетическая энергия поступательного движения молекулы азота, находящегося при нормальных условиях в сосуде, движущемся со скоростью 86 м/с при внезапной остановке сосуда?