7. 5 Проверка соответствия экспериментальных данных нормальному закону распределения

При статической обработке результатов измерений особую роль играет проверка соответствия распределения случайных величин нормальному закону, которому чаще всего подчиняются результаты большинства случайных измерений, что необходимо для обоснованного выбора доверительных границ результатов измерений. В наи­большей степени этой цели соответствует критерий Пирсона , который применяется при количестве измерений свыше 40.

При измерении плотности грунта было сделано 80 измерений (таблица 4)

Таблица 4

Результаты измерений плотности грунта (г/см3)
№	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
1
2
3
4
5

Все результаты измерений оказались лежащими в диапазоне ... , т.е. зона разброса результатов (размах) составляет

.

В этом случае весь диапазон целесообразно распределить на 10 интервалов рав­ной длины.

Длина интервала

,

где число интервалов

.

Определение границ интервалов производится путем последовательного при­бавления к минимальному результату измерения расчетной длины интервала.

и т.д.

Границы интервалов заносятся в таблицу 5, в которой проводятся дальнейшие расчеты.

Таблица 5

№ Инт.	Интервалы действительных значений	Среднее значение интервала	Число измерений в интервале (экспериментальная частота)	Частость	Отклонение от среднего значения
1
2
3
4
5
6
7
8
9
10
			80

Статистическое среднеквадратичное отклонение

Таблица 6

№ Инт	Интервалы действии-тельных значений	Нормированное отклонение от среднего арифметического	Значение функции плотности вероятностей для нормального закона	Плотность в серединах интервалов	Теоретическая частота	Показатель разности частот
1
2
3
4
5
6
7
8
9
10

Гипотеза о том, что опытное распределение значений можно считать нормальным подтверждается, если соблюдается условие

< <

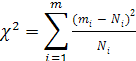
где экспериментальные и теоретические значения частот n в i-том интервале;

.

Задавая уровень значимости значения находят по таблицам интегральной функции распределения для чего определяется число степеней свободы

Число степеней свободы

где

Поскольку число наблюдений в третьем и четвертом интервалах меньше пяти, то 2-ой и 3-й интервал объединен в один, а также 4-ый и 5-ый. Поэтому

Из полученных значений делаем вывод, что гипотеза о совпадении отвергается (принимается), так как не соблюдается (соблюдается) условие

< < = .