МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА”

Комп’ютерна графіка

Методичні вказівки

до виконання лабораторних робіт

для студентів базового напряму «Видавничо-поліграфічна справа» спеціальності «Комп’ютеризовані технології та системи видавничо-поліграфічного виробництва» та напряму «Комп’ютерні науки» спеціальності «Автоматизовані системи управління»

Затверджено на засіданні кафедри

Інформаційні технології видавничої справи

Протокол № 7-11/12 від 21 лютого 2012 р.

Львів – 2012

Комп’ютерна графіка: Методичні вказівки до лабораторних робіт для студентів «Видавничо-поліграфічна справа» (шифр - 051501) та “Комп‘ютерні науки” (шифр - 050101) / Укл.: О.Я. Різник - Львів: Видавництво Національного університету “Львівська політехніка”, 2012. - 92 с.

Укладач: Різник О.Я., к.т.н., доц.

Відповідальний за випуск: Різник О. Я., к. т. н., доц.

Рецензент: Цмоць І.Г., д.т.н., проф.

Лабораторна робота №1

Основи комп’ютерної графіки.

Робота в декартовій системі координат

Мета: Ознайомлення з основами комп‘ютерної графіки.

Теоретичні основи

1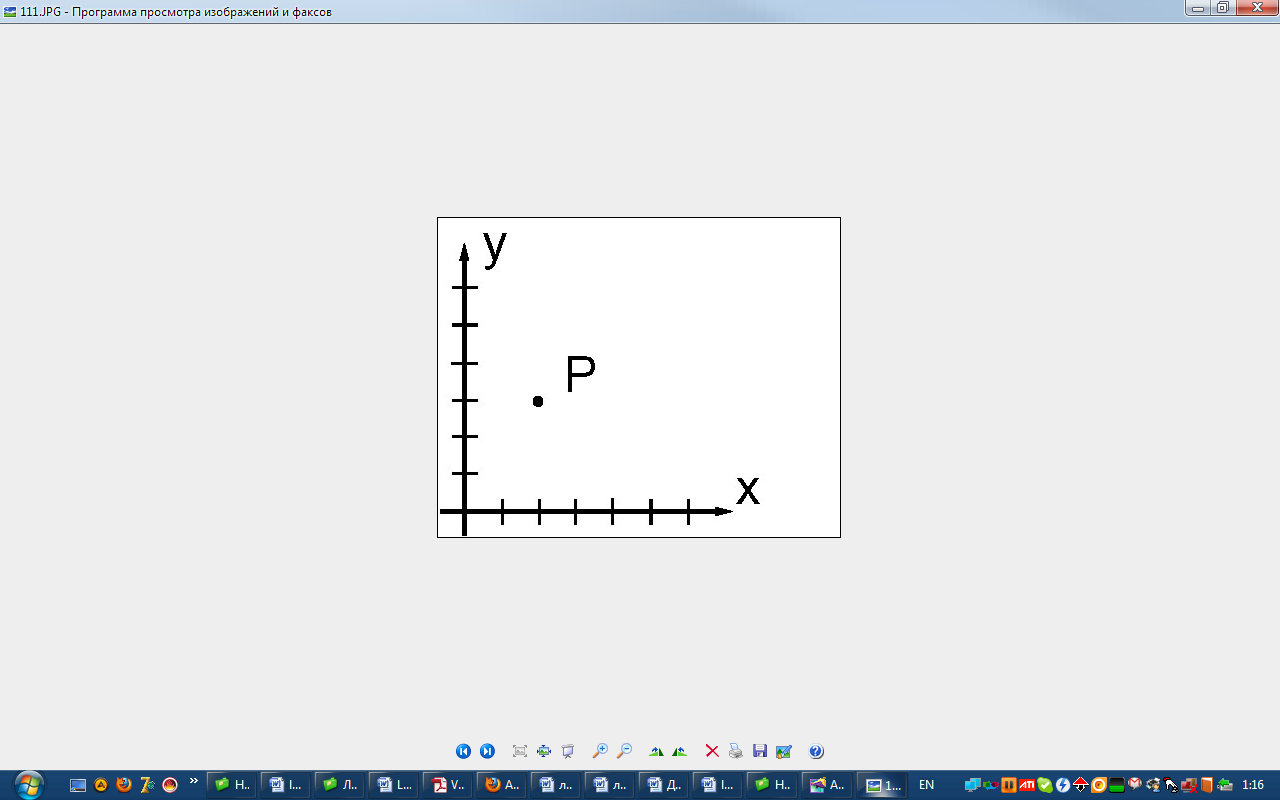 .1 Представлення точок

Точка задається за допомогою двох

значень (x y) , наприклад, (2 3).

1.2 Перетворення точок

Розглянемо результати матричного

множення , що визначає точку Р, і матриці перетворення 2х2 загального виду:

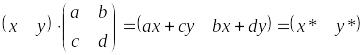
Дослідимо декілька часткових випадків.

1) а=d=1 і c=b=0. Змін не відбувається

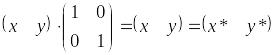
2 ) d=1, b=c=0. Зміна масштабу по осі x

3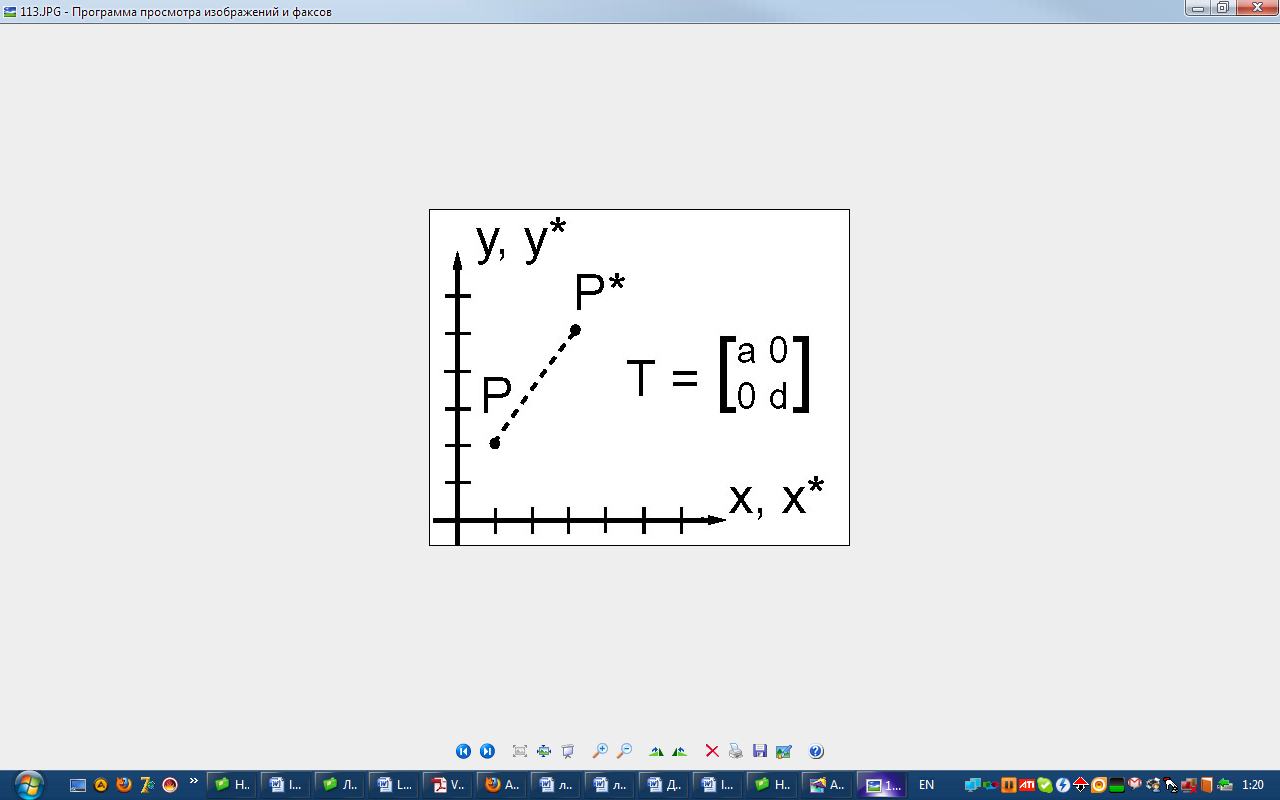 ) b=c=0. Зміна масштабу по осях x і y

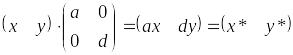
4) b=c=0, d=1, a=-1. Відображення координат відносно осі y

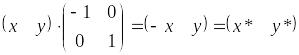
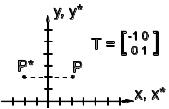
5) b=c=0, a=d<0. Відображення відносно початку координат

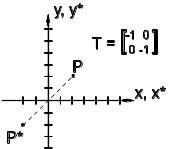
6) а=d=1, c=0. Зсув

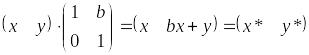
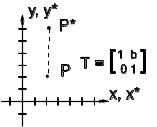
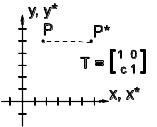
1.3 Перетворення прямих ліній (відрізків)

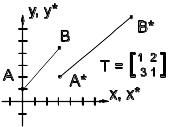
Будь-яка пряма будується за допомогою двох точок, наприклад, А і В.

Нехай точки А і В задані координатами – А(0,1) і В(2,3).

Матриця ж перетворення, задана такими значеннями

.

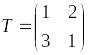В результаті декартового добутку вектора-точки на матрицю перетворення одержимо:

,

.

Тепер координати точок прямої мають вигляд такий А(3, 1) та В(11, 7).

Результат показано на мал.

1.4 Обертання

Розглянемо плоский трикутник ABC. Нехай координати трикутника задані такими значеннями, А(3, 1), В(6, 1) та С(6, 4).

Матриця перетворення для повороту на 90° проти годинникової стрілки, виглядає так

Після декартового добутку одержимо матрицю:

.

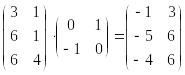
В результаті отримаємо трикутник

A*B*C*.

Матриця перетворення для повороту

н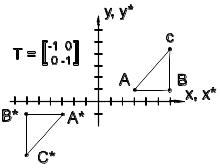 а 180° проти годинникової стрілки,

виглядає так

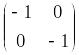
Після декартового добутку одержимо матрицю:

.

В результаті отримаємо трикутник

A*B*C*.

Матриця перетворення для повороту на 270° проти годинникової стрілки, виглядає так:

.

П ісля декартового добутку одержимо матрицю:

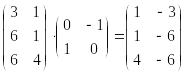
В результаті отримаємо трикутник А*B*C*.