- •З Стор. Міст.
- •Тема 1. Вступ в розділ «Динаміка». Динаміка точки
- •§ 1.1. Предмет і задачі розділу “Динаміка”
- •§ 1.2. Закони класичної механіки.
- •1 Закон (інерції)
- •3 Закон (дії протидії)
- •2 Закон (основний)
- •Динаміка точки.
- •§ 1.3. Диференціальні рівняння руху матеріальної точки. Дві задачі динаміки точки.
- •Рекомендації для практичних занять на тему “Друга задача динаміки точки”
- •Питання для самоконтролю.
- •Динаміка механічної системи.
- •Тема 2. Вступ до “Динаміки механічної системи”.
- •§ 2.1. Структурні та інерційні характеристики механічної системи.
- •Н айменший осьовий момент інерції тіла відносно осі, яка проходить через центр мас.
- •§ 2.2. Осьові моменти інерції деяких твердих однорідних тіл, масою m.
- •§ 2.3. Класифікація сил, їх властивості.
- •§ 2.4. Динамічні рівняння руху системи (для теоретичної моделі).
- •Або в проекціях на осі координат
- •Питання для самоконтролю.
- •Розділ “Загальні теореми динаміки”.
- •Тема 3. Перша загальна теорема динаміки: про зміну кількості руху, або про рух центру мас системи.
- •§ 3.1. Кількість руху точки, системи.
- •§3.2 Теорема про зміну кількості руху (теорема імпульсів).
- •§ 3.3 Закон збереження кількості руху механічної системи ( частинний випадок теореми).
- •Питання для самоконтролю.
- •Тема 4. Теорема про зміну кінетичного моменту. Динамічні рівняння руху твердих тіл.
- •§4.1 Кінетичний момент матеріальної точки та механічної системи.
- •§4.1.1 Кінетичний момент відносно центру.
- •§4.1.2. Кінетичний момент відносно осі.
- •П роекція кінетичного моменту матеріальної точки відносно деякого центру на вісь, яка проходить через цей центр, дорівнює кінетичному моментові точки відносно цієї осі.
- •§4.2. Кінетичний момент тіла відносно осі обертання.
- •§4.3. Теорема про зміну кінетичного моменту.
- •§ 4.4. Диференціальні рівняння простих рухів.
- •§4.5. Динамічні рівняння плоско–паралельного руху твердого тіла.
- •§4.5.1. Теорема про зміну кінетичного моменту механічної системи при відносному русі.
- •§4.5.2. Динамічні рівняння плоского руху.
- •§ 4.6. Наслідки теорем. Закони збереження кінетичних моментів.
- •Рекомендації для практичних занять на тему
- •Питання для самоконтролю.
- •Тема 5. Теорема про зміну кінетичної енергії механічної системи.
- •§ 5.1. Робота і потужність сили та пари сил.
- •§5.2. Приклади обчислення робіт.
- •§5.2.1. Робота сили тяжіння (сили ваги).
- •§5.2.2. Робота сили пружності.
- •§5.2.3. Робота постійної сили.
- •§5.3. Кінетична енергія.
- •§5.3.1. Теорема Кьоніга про кінетичну енергію.
- •§5.3.2. Кінетична енергія твердих тіл.
- •§5.4. Теорема про зміну кінетичної енергії.
- •§5.4.1. Теорема в випадку незмінюваної механічної системи.
- •§5.4.2. Теорема в випадку системи з ідеальними в’язями.
- •§5.5. Інтегральна форма теореми про зміну кінетичної енергії системи.
- •§5.6. Теорема про зміну кінетичної енергії в випадку потенціального силового поля.
- •Рекомендації до практичних занять на тему “ Теорема про зміну кінетичної енергії”.
- •Питання для самоконтролю.
- •Розділ Принципи механіки.
- •Тема 6. Принцип д`Аламбера (умовного зрівноваження сил).
- •§6.1. Принцип д`Аламбера для матеріальної точки.
- •§6.2. Принцип д`Аламбера для механічної системи
- •§6.3. Головний вектор і головний момент сил інерції.
- •§6.4. Головні вектори та головні моменти д’Аламберових сил інерції твердих тіл. (законспектувати самостійно).
- •Рекомендації по застосуванню принципу д’Аламбера (методу кінетостатики)
- •Питання для самоконтролю.
- •Тема 7. Принцип можливих переміщень. Загальне рівняння динаміки.
- •§ 7.1. Класифікація в’язей.
- •§ 7.2. Можливі переміщення.
- •§ 7.3. Число ступенів вільності.
- •§ 7.4. Можлива робота. Ідеальні в’язі.
- •§ 7.5. Принцип можливих переміщень.
- •§ 7.6. Застосування принципу можливих переміщень.
- •§ 7.6.1 Для визначення однієї з активних сил, що діють на систему з одним ступенем вільності.
- •§ 7.6.2. Для визначення реакцій в’язі складеної конструкції.
- •§ 7.7. Загальне рівняння динаміки, або принцип д’Аламбера – Лагранжа.
- •Рекомендації до практичних занять на тему:
- •Питання для самоконтролю.
- •Тема 8. Аналітична механіка в узагальнених координатах.
- •§ 8.1. Узагальнені координати.
- •§ 8.2. Узагальнені сили.
- •§ 8.2.1. Практичний спосіб обчислення - “j”-ої узагальненої сили.
- •§ 8.2.2. Обчислення узагальненої потенціальної сили.
- •§ 8.3. Принцип можливих переміщень в узагальнених координатах.
- •§ 8.4. Загальне рівняння динаміки в узагальнених координатах, або рівняння Лагранжу іі роду.
- •§ 8.5. Рівняння Лагранжу іі роду для консервативних систем.
- •§ 8.6. Застосування рівнянь Лагранжу іі роду для складання диференціальних рівнянь руху практичної моделі механічної системи.
- •Питання для самоконтролю.
- •Тема 9. Динамічне рівняння руху машини.
- •§ 9.2. Зведення сил.
- •§ 9.3. Складання динамічного рівняння руху машини.
- •Розділ. Малі лінійні коливання механічної системи.
- •Тема 10. Вступ в теорію малих лінійних коливань.
- •§ 10.1. Види механічних коливань.
- •§ 10.2. Поняття про стійкість рівноваги. Теорема Лагранжа – Діріхле.
- •§ 10.3. Про особливості методу вивчення малих коливань системи.
- •Метод вивчення.
- •Тема 11. Вільні (власні) коливання механічної системи з одним ступенем вільності.
- •§ 11.1. Постановка задачі Диференціальне рівняння руху.
- •§ 11.2. Закон малих власних вільних коливань.
- •§ 11.3. Властивості руху.
- •Основні властивості власних коливань.
- •Тема 12. Вплив лінійного опору на лінійні власні коливання системи з одним ступенем вільності.
- •§ 12.1. Узагальнена сила опору. Функція Релея.
- •§ 12.2. Постановка задачі. Диференціальне рівняння руху.
- •§ 12.3. Інтегрування диференціального рівняння руху.
- •§ 12.4. Властивості руху при малому опорі.
- •§ 12.5. Аперіодичний рух
- •Тема 13. Вимушені коливання механічної системи з одним ступенем вільності (без врахування опору).
- •§ 13.1. Постановка задачі.
- •§ 13.2. Диференціальне рівняння вимушених коливань.
- •§ 13.3. Рівняння (закон) руху.
- •§ 13.4. Властивості вимушених коливань.
- •§ 13.5. Випадок резонансу.
- •Тема 14. Вимушені коливання механічної системи з одним ступенем вільності з врахуванням лінійного опору.
- •§ 14.1. Постановка задачі.
- •§ 14.2. Інтегрування диференціального рівняння руху. Закон руху.
- •§ 14.3. Властивості вимушених коливань.
- •§ 14.4. Залежність амплітуди та фази вимушених коливань від частоти та фази збурюючої сили.
- •Висновки.
- •Питання для самоконтролю.
Н айменший осьовий момент інерції тіла відносно осі, яка проходить через центр мас.
§ 2.2. Осьові моменти інерції деяких твердих однорідних тіл, масою m.
|
|
|
|
|
|
|
|
Т
|
iz – радіус інерції тіла, характеризує форму тіла (визначається експериментально), відстань від осі до точки, в якій треба зосередити масу тіла, щоб момент інерції точки дорівнював моментові інерції тіла. |
Самостійно законспектувати вивод формул [1] § 36
[2] Розд. 3, гл. 4, § 4
§ 2.3. Класифікація сил, їх властивості.
Внутрішніми силами називають сили взаємодії між елементами механічної системи. Вони мають дві властивості:
Головний вектор внутрішніх сил, що діють на систему дорівнює нулеві;
![]()
![]()
Головний момент внутрішніх сил, відносно довільного центру або осі дорівнює нулеві.
![]()





![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() - згідно закону рівності дії протидії.
- згідно закону рівності дії протидії.
Зовнішніми силами називають сили, з якими елементи даної системи взаємодіють з тілами, що не належать до даної системи.
П





![]()
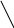

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() риклад.
Маємо кінематичну схему двигуна
внутрішнього згорання. До кривошипу ОА
прикладений рушійний момент Мр,
до повзуна 3 – сила тертя
.
риклад.
Маємо кінематичну схему двигуна
внутрішнього згорання. До кривошипу ОА
прикладений рушійний момент Мр,
до повзуна 3 – сила тертя
.
О
 б`єкт
вивчення: система, що складається з тіл
1,2,3.
б`єкт
вивчення: система, що складається з тіл
1,2,3.
Самостійно визначити зовнішні та внутрішні сили, активні та реакції в’язей (в розділі „Статика” була така класифікація).
А
?
![]() :
:
Реакції в`язей![]() :
:
Зовнішні![]() :
:
Внутрішні![]() :
:
§ 2.4. Динамічні рівняння руху системи (для теоретичної моделі).
|
![]() -
рівнодійна зовнішніх сил,
-
рівнодійна зовнішніх сил,
![]() -
рівнодійна внутрішніх сил, прикладених
до “k”-ої точки.
-
рівнодійна внутрішніх сил, прикладених
до “k”-ої точки.
Запишемо диференціальні рівняння руху усіх точок системи
Векторна форма
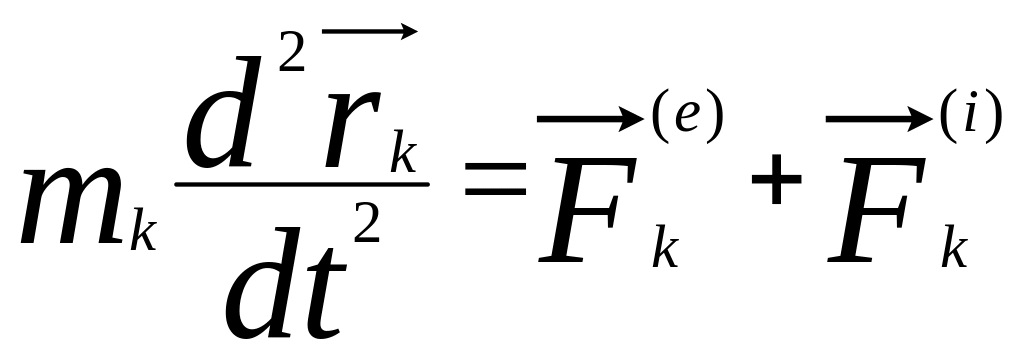 ,к=1,2...n.
,к=1,2...n.
Або в проекціях на осі координат
![]()
![]()
Як застосувати ці рівняння?
Система рівнянь (2.7) для практичних моделей не застосовується з таких причин:
розв’язок цих рівнянь - це громіздка математична задача, бо маємо систему 3n диференціальних рівнянь 2-ого порядку;
в правих частинах цих рівнянь маємо внутрішні сили, які завжди не відомі;
немає практичної потреби знати, як рухається кожна точка механічної системи.
Але ці рівняння були застосовані для вивчення планет Сонячної системи.
Ми готуємось вивчати рух реальних машин і механізмів.
Застосуємо другий підхід до складання Д.Р.Р. механічної системи для практичної моделі, а саме, скористаємось загальними теоремами динаміки.
Питання для самоконтролю.
Що називається механічною системою?
Як класифікуються сили, що діють на точки механічної системи?
Яким умовам задовольняють внутрішні сили, що діють на точки механічної системи?
Що називають центром мас механічної системи?
Запишіть формули, за допомогою яких визначаються координати центра мас механічної системи.
Що називається моментом інерції системи відносно осі?
Запишіть формулу, за допомогою якої визначається момент інерції системи відносно початку координат.
Сформулюйте теорему Гюйгенса-Штейнера.
Які осі називаються головними осями інерції?


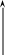


 днорідний
стержень
днорідний
стержень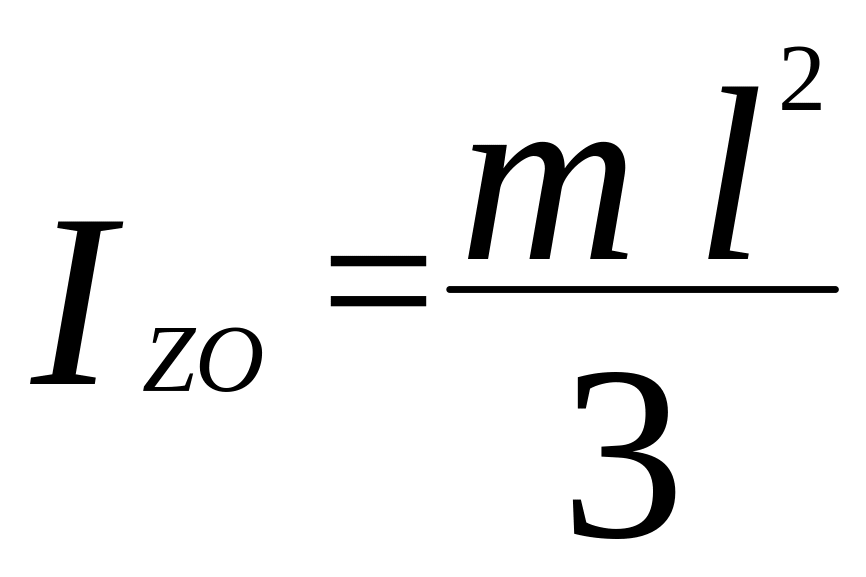
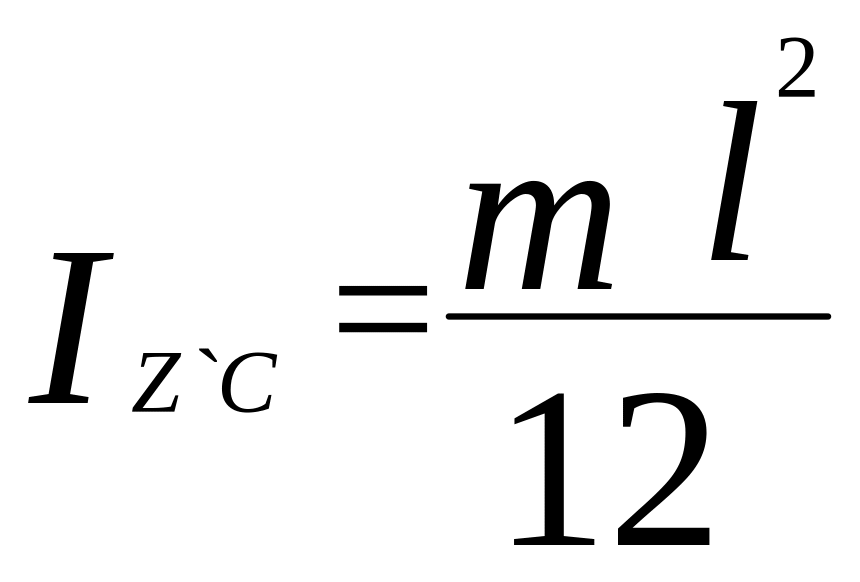


 ільце
ільце
 иск
иск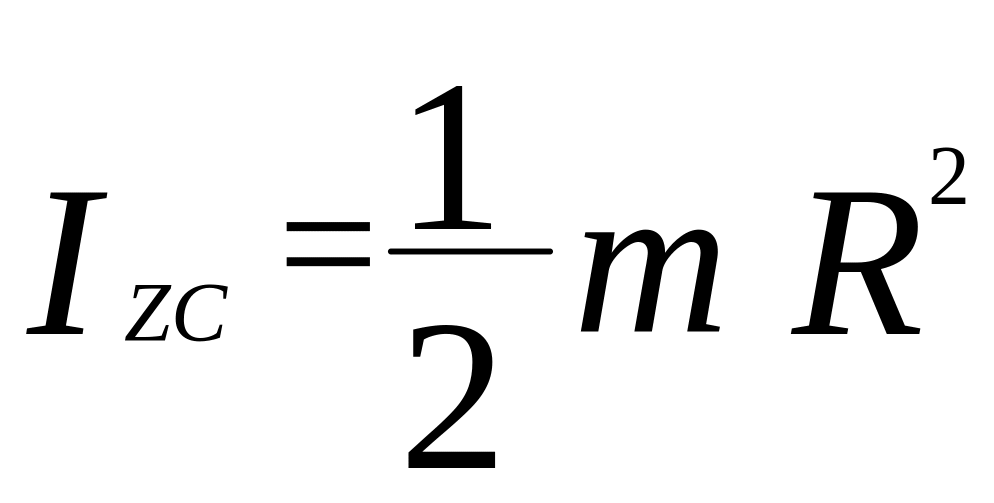


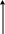
 ластина
ластина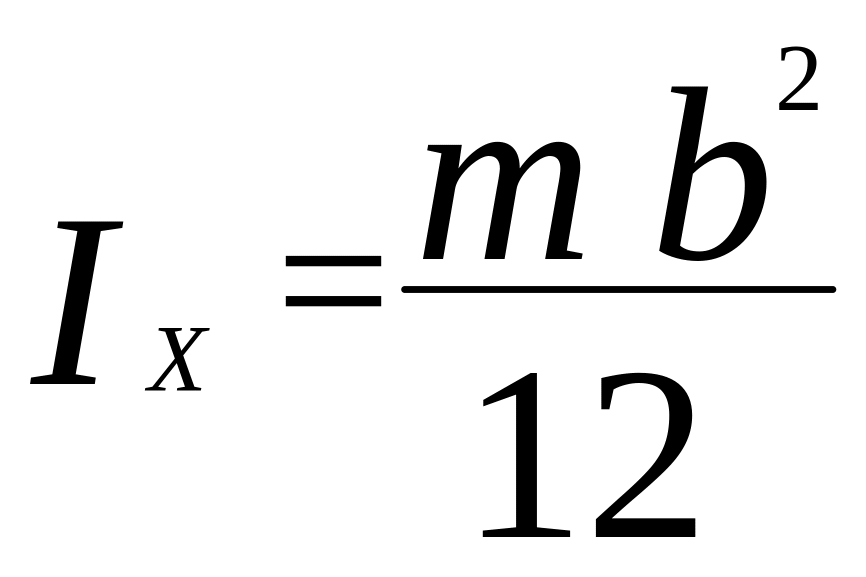
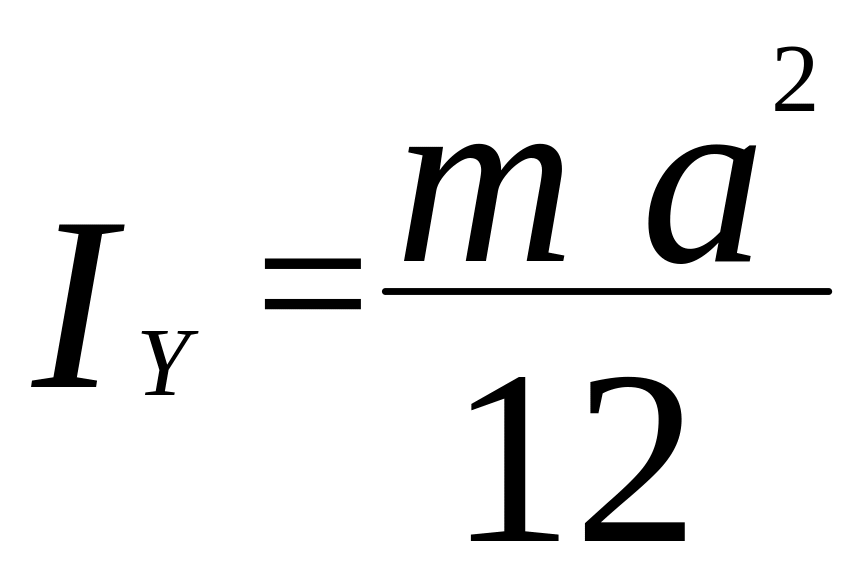
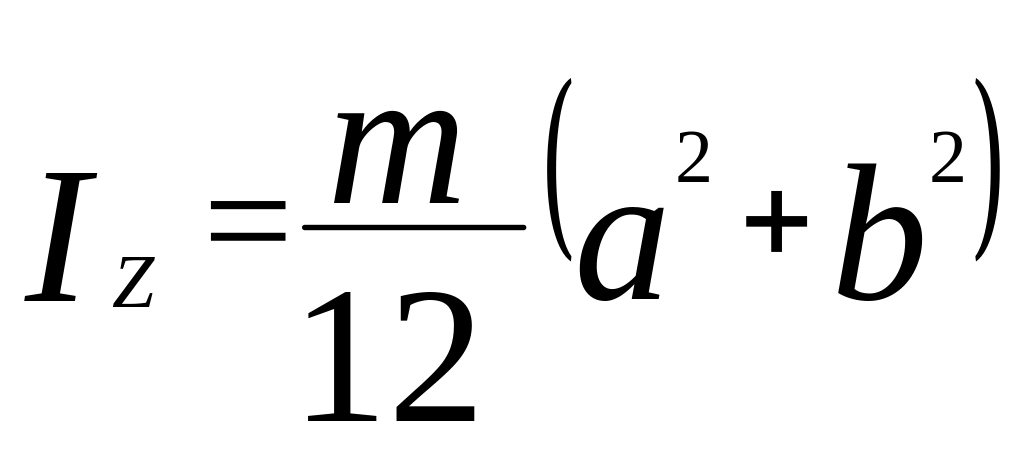
 іло
довільної форми
іло
довільної форми