
- •З Стор. Міст.
- •Тема 1. Вступ в розділ «Динаміка». Динаміка точки
- •§ 1.1. Предмет і задачі розділу “Динаміка”
- •§ 1.2. Закони класичної механіки.
- •1 Закон (інерції)
- •3 Закон (дії протидії)
- •2 Закон (основний)
- •Динаміка точки.
- •§ 1.3. Диференціальні рівняння руху матеріальної точки. Дві задачі динаміки точки.
- •Рекомендації для практичних занять на тему “Друга задача динаміки точки”
- •Питання для самоконтролю.
- •Динаміка механічної системи.
- •Тема 2. Вступ до “Динаміки механічної системи”.
- •§ 2.1. Структурні та інерційні характеристики механічної системи.
- •Н айменший осьовий момент інерції тіла відносно осі, яка проходить через центр мас.
- •§ 2.2. Осьові моменти інерції деяких твердих однорідних тіл, масою m.
- •§ 2.3. Класифікація сил, їх властивості.
- •§ 2.4. Динамічні рівняння руху системи (для теоретичної моделі).
- •Або в проекціях на осі координат
- •Питання для самоконтролю.
- •Розділ “Загальні теореми динаміки”.
- •Тема 3. Перша загальна теорема динаміки: про зміну кількості руху, або про рух центру мас системи.
- •§ 3.1. Кількість руху точки, системи.
- •§3.2 Теорема про зміну кількості руху (теорема імпульсів).
- •§ 3.3 Закон збереження кількості руху механічної системи ( частинний випадок теореми).
- •Питання для самоконтролю.
- •Тема 4. Теорема про зміну кінетичного моменту. Динамічні рівняння руху твердих тіл.
- •§4.1 Кінетичний момент матеріальної точки та механічної системи.
- •§4.1.1 Кінетичний момент відносно центру.
- •§4.1.2. Кінетичний момент відносно осі.
- •П роекція кінетичного моменту матеріальної точки відносно деякого центру на вісь, яка проходить через цей центр, дорівнює кінетичному моментові точки відносно цієї осі.
- •§4.2. Кінетичний момент тіла відносно осі обертання.
- •§4.3. Теорема про зміну кінетичного моменту.
- •§ 4.4. Диференціальні рівняння простих рухів.
- •§4.5. Динамічні рівняння плоско–паралельного руху твердого тіла.
- •§4.5.1. Теорема про зміну кінетичного моменту механічної системи при відносному русі.
- •§4.5.2. Динамічні рівняння плоского руху.
- •§ 4.6. Наслідки теорем. Закони збереження кінетичних моментів.
- •Рекомендації для практичних занять на тему
- •Питання для самоконтролю.
- •Тема 5. Теорема про зміну кінетичної енергії механічної системи.
- •§ 5.1. Робота і потужність сили та пари сил.
- •§5.2. Приклади обчислення робіт.
- •§5.2.1. Робота сили тяжіння (сили ваги).
- •§5.2.2. Робота сили пружності.
- •§5.2.3. Робота постійної сили.
- •§5.3. Кінетична енергія.
- •§5.3.1. Теорема Кьоніга про кінетичну енергію.
- •§5.3.2. Кінетична енергія твердих тіл.
- •§5.4. Теорема про зміну кінетичної енергії.
- •§5.4.1. Теорема в випадку незмінюваної механічної системи.
- •§5.4.2. Теорема в випадку системи з ідеальними в’язями.
- •§5.5. Інтегральна форма теореми про зміну кінетичної енергії системи.
- •§5.6. Теорема про зміну кінетичної енергії в випадку потенціального силового поля.
- •Рекомендації до практичних занять на тему “ Теорема про зміну кінетичної енергії”.
- •Питання для самоконтролю.
- •Розділ Принципи механіки.
- •Тема 6. Принцип д`Аламбера (умовного зрівноваження сил).
- •§6.1. Принцип д`Аламбера для матеріальної точки.
- •§6.2. Принцип д`Аламбера для механічної системи
- •§6.3. Головний вектор і головний момент сил інерції.
- •§6.4. Головні вектори та головні моменти д’Аламберових сил інерції твердих тіл. (законспектувати самостійно).
- •Рекомендації по застосуванню принципу д’Аламбера (методу кінетостатики)
- •Питання для самоконтролю.
- •Тема 7. Принцип можливих переміщень. Загальне рівняння динаміки.
- •§ 7.1. Класифікація в’язей.
- •§ 7.2. Можливі переміщення.
- •§ 7.3. Число ступенів вільності.
- •§ 7.4. Можлива робота. Ідеальні в’язі.
- •§ 7.5. Принцип можливих переміщень.
- •§ 7.6. Застосування принципу можливих переміщень.
- •§ 7.6.1 Для визначення однієї з активних сил, що діють на систему з одним ступенем вільності.
- •§ 7.6.2. Для визначення реакцій в’язі складеної конструкції.
- •§ 7.7. Загальне рівняння динаміки, або принцип д’Аламбера – Лагранжа.
- •Рекомендації до практичних занять на тему:
- •Питання для самоконтролю.
- •Тема 8. Аналітична механіка в узагальнених координатах.
- •§ 8.1. Узагальнені координати.
- •§ 8.2. Узагальнені сили.
- •§ 8.2.1. Практичний спосіб обчислення - “j”-ої узагальненої сили.
- •§ 8.2.2. Обчислення узагальненої потенціальної сили.
- •§ 8.3. Принцип можливих переміщень в узагальнених координатах.
- •§ 8.4. Загальне рівняння динаміки в узагальнених координатах, або рівняння Лагранжу іі роду.
- •§ 8.5. Рівняння Лагранжу іі роду для консервативних систем.
- •§ 8.6. Застосування рівнянь Лагранжу іі роду для складання диференціальних рівнянь руху практичної моделі механічної системи.
- •Питання для самоконтролю.
- •Тема 9. Динамічне рівняння руху машини.
- •§ 9.2. Зведення сил.
- •§ 9.3. Складання динамічного рівняння руху машини.
- •Розділ. Малі лінійні коливання механічної системи.
- •Тема 10. Вступ в теорію малих лінійних коливань.
- •§ 10.1. Види механічних коливань.
- •§ 10.2. Поняття про стійкість рівноваги. Теорема Лагранжа – Діріхле.
- •§ 10.3. Про особливості методу вивчення малих коливань системи.
- •Метод вивчення.
- •Тема 11. Вільні (власні) коливання механічної системи з одним ступенем вільності.
- •§ 11.1. Постановка задачі Диференціальне рівняння руху.
- •§ 11.2. Закон малих власних вільних коливань.
- •§ 11.3. Властивості руху.
- •Основні властивості власних коливань.
- •Тема 12. Вплив лінійного опору на лінійні власні коливання системи з одним ступенем вільності.
- •§ 12.1. Узагальнена сила опору. Функція Релея.
- •§ 12.2. Постановка задачі. Диференціальне рівняння руху.
- •§ 12.3. Інтегрування диференціального рівняння руху.
- •§ 12.4. Властивості руху при малому опорі.
- •§ 12.5. Аперіодичний рух
- •Тема 13. Вимушені коливання механічної системи з одним ступенем вільності (без врахування опору).
- •§ 13.1. Постановка задачі.
- •§ 13.2. Диференціальне рівняння вимушених коливань.
- •§ 13.3. Рівняння (закон) руху.
- •§ 13.4. Властивості вимушених коливань.
- •§ 13.5. Випадок резонансу.
- •Тема 14. Вимушені коливання механічної системи з одним ступенем вільності з врахуванням лінійного опору.
- •§ 14.1. Постановка задачі.
- •§ 14.2. Інтегрування диференціального рівняння руху. Закон руху.
- •§ 14.3. Властивості вимушених коливань.
- •§ 14.4. Залежність амплітуди та фази вимушених коливань від частоти та фази збурюючої сили.
- •Висновки.
- •Питання для самоконтролю.
§ 14.2. Інтегрування диференціального рівняння руху. Закон руху.
Диференціальне рівняння (14.2) – ЛНДР – лінійне неоднорідне диференціальне рівняння ІІ порядку з постійними коефіцієнтами. Його розв’язок
![]()
![]()
Де: – загальний розв’язок однорідного рівняння
![]()
Згадаємо тему 11, – залежить від співвідношення між n та ω.
Р![]() озглянемо
випадок малого опору n<ω,
тоді
озглянемо
випадок малого опору n<ω,
тоді
![]() де
де
![]()
![]() – частинний розв’язок рівняння (14.2),
вид якого диктується його правою
частиною. В даному випадку
– частинний розв’язок рівняння (14.2),
вид якого диктується його правою
частиною. В даному випадку
Ч![]()
![]() ерез
те, що з часом власні коливання зникають
(бо є співмножник
ерез
те, що з часом власні коливання зникають
(бо є співмножник
![]() ),
можна вважати, що залишаться тільки
вимушені коливання, тобто частинний
розв’язок
),
можна вважати, що залишаться тільки
вимушені коливання, тобто частинний
розв’язок
З![]()
![]() найдемо
постійну В. Для цього підставимо (14.5) в
(14.2), отримавши похідні
найдемо
постійну В. Для цього підставимо (14.5) в
(14.2), отримавши похідні
Праву частину рівняння (14.2) перетворимо
так
![]() Після
підстановки в рівняння (14.2), маємо
Після
підстановки в рівняння (14.2), маємо
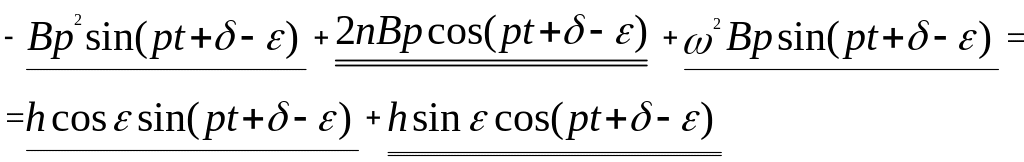
М
![]()

![]()
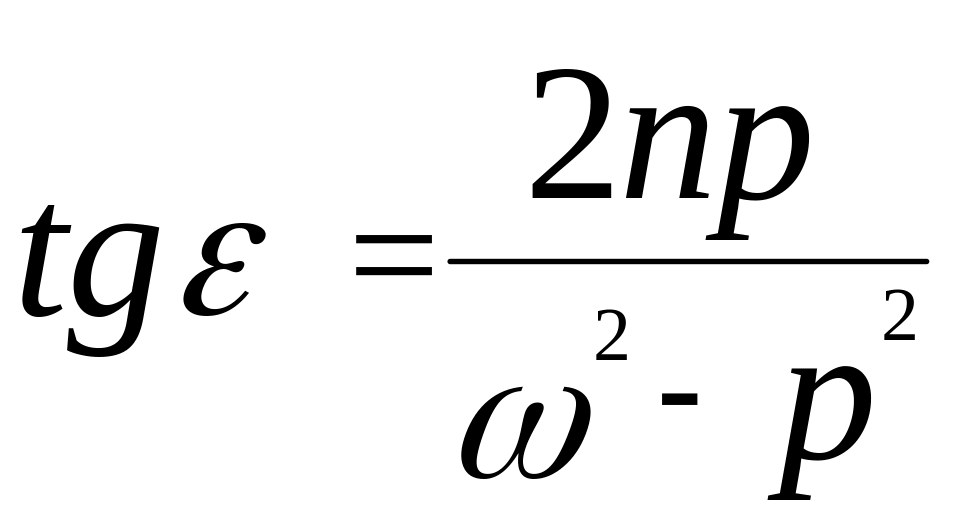
![]() аємо,
зібравши коефіцієнти при
аємо,
зібравши коефіцієнти при
![]() та
при
та
при
![]() :
:
М![]() ожна
вважати, що для t
далекого від початкового
ожна
вважати, що для t
далекого від початкового

Аналізуючи (14.8) відмітимо властивості вимушених коливань.
§ 14.3. Властивості вимушених коливань.
1. Навіть при наявності опору вимушені коливання носять періодичний, незатухаючий характер.
2. Частота і період вимушених коливань дорівнюють частоті і періоду збурюючої сили.
3. Амплітуда В (формула (14.6)) і початкова фаза ε (формула (14.7)) не залежать від початкових умов, а залежать від: вихідних параметрів а і с, частоти р збурюючої сили та сили опору. Амплітуда залежить ще від амплітуди збурюючої сили Н.
4. Навіть при резонансі (ω=р) при
наявності лінійного опору амплітуда
має конкретне значення В≠∞. і не змінюється.
і не змінюється.
Далі розглянемо окремо важливе для інженерної практики питання.
§ 14.4. Залежність амплітуди та фази вимушених коливань від частоти та фази збурюючої сили.
Розглянемо більш детально формулу амплітуди вимушених коливань.
Перетворимо (14.6) так: поділимо на ω2 чисельник і знаменник
П означимо:
означимо:
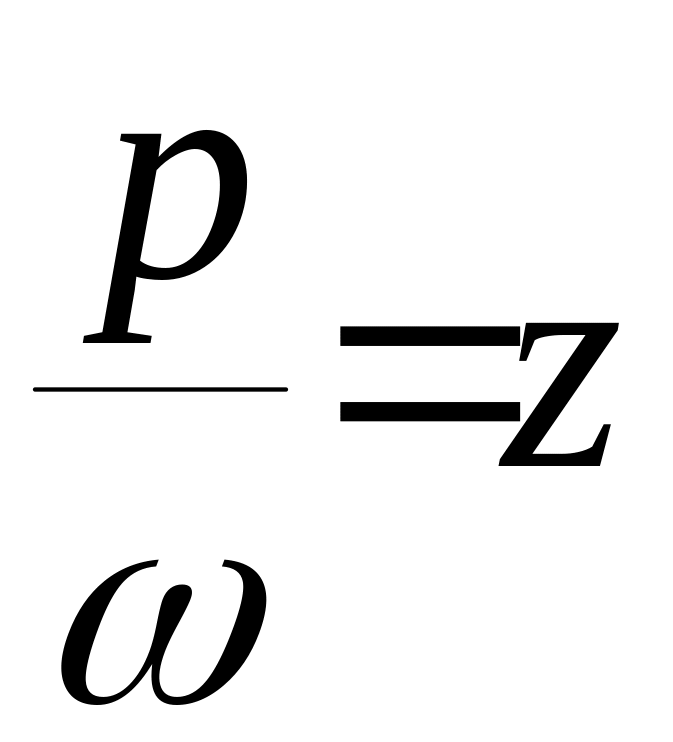 – коефіцієнт розладнання,
– коефіцієнт розладнання,
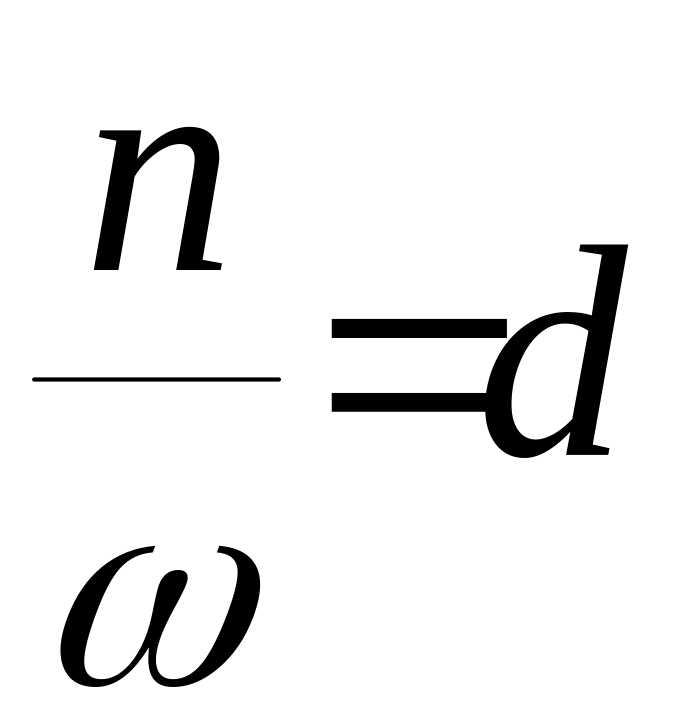 – відносний коефіцієнт опору,
– відносний коефіцієнт опору,
n
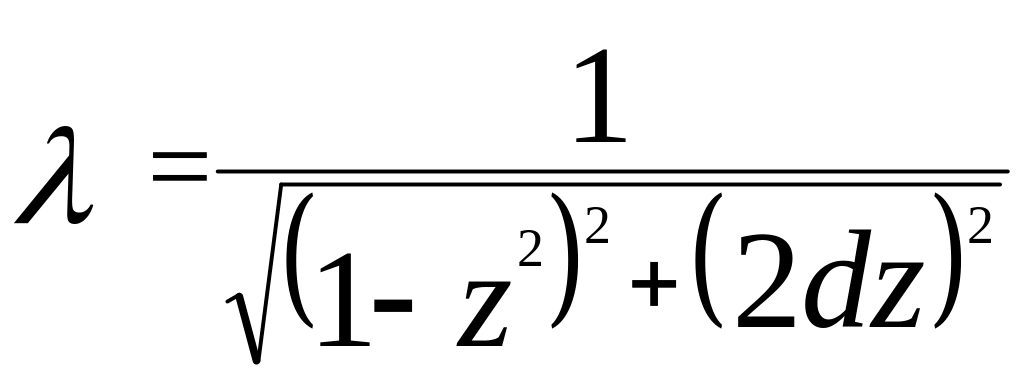
![]() <ω,
0<d<1
<ω,
0<d<1
- коефіцієнт динамічності.
З’ясуємо зміст
![]() .
Якщо на систему діє постійна сила Н,
що дорівнює максимуму збурюючої сили,
тоді
.
Якщо на систему діє постійна сила Н,
що дорівнює максимуму збурюючої сили,
тоді
![]() .
Частинний розв’язок
.
Частинний розв’язок
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
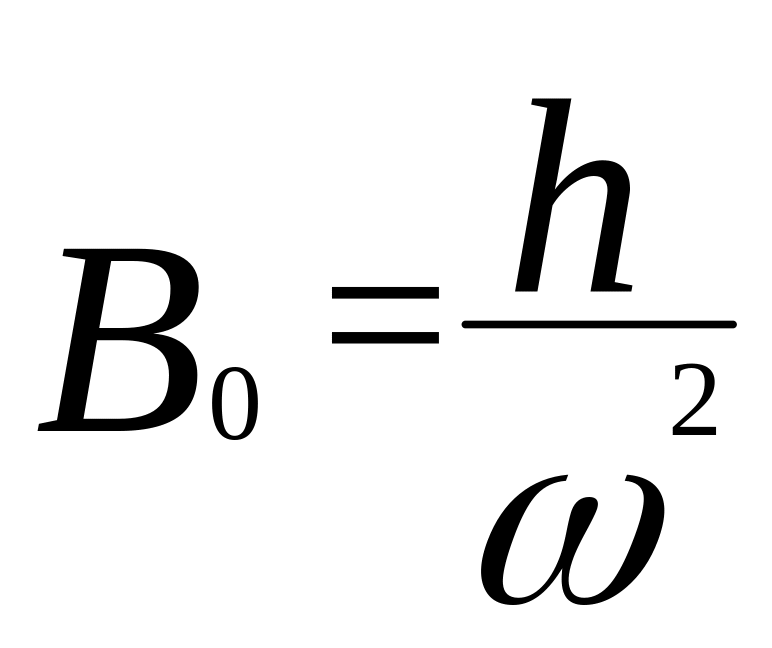 – відхилення системи в положенні
рівноваги під дією постійні сили, що
дорівнює амплітуді збурюючої сили Тоді
– відхилення системи в положенні
рівноваги під дією постійні сили, що
дорівнює амплітуді збурюючої сили Тоді
 – відношення динамічної амплітуди
до статичної називають: коефіцієнт
динамічності.
– відношення динамічної амплітуди
до статичної називають: коефіцієнт
динамічності.
З








![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 амість
задачі залежність В(р) вивчимо залежність
λ(z) коефіцієнта динамічності
від коефіцієнта розладнання. Покажемо
графік функції (14.9).
амість
задачі залежність В(р) вивчимо залежність
λ(z) коефіцієнта динамічності
від коефіцієнта розладнання. Покажемо
графік функції (14.9).
Дослідимо знаменник
![]() на екстремум. Для цього отримаємо похідну
на екстремум. Для цього отримаємо похідну
![]() ,
,![]() ,
,
П![]()
![]() рирівняємо
рирівняємо![]() ,
тобто знайдемо значення z
при яких буде екстремум
,
тобто знайдемо значення z
при яких буде екстремум
![]()
Висновки.
1.
При наявності лінійного опору найбільше
значення λ досягає не при
z=1, тобто не при резонансі,
а при z<1,
якщо
![]() ,
а саме при
,
а саме при
![]()
2. Чим менший опір d, тим більша λmax. λ зростає тим швидше, чим менше d.
3. Для великих частот збурюючої сили амплітуда вимушених коливань невелика.
4. Сили опору мають вплив на амплітуду лише поблизу резонансної зони, розміром в 30%.
5. Для частот, що знаходяться за тридцятипроцентною резонансною зоною, вплив сил опору малопомітний. Тобто для z<0,7; z>1,3, коефіцієнт динамічності λ≤2.
6. Для d>0,7 максимальне значення амплітуди дорівнює її статичному значенню, і резонансу не буває.
Дослідимо зсув фаз вимушених коливань відносно збурюючої сили, тобто формулу(14.7)
Д







![]()
![]()
![]()
![]()
![]() ля
z<1
ля
z<1

Д
ля
z=1

Д ля
z>1
ля
z>1

Звертаю увагу на те, що як і в випадку відсутності лінійного опору (рис.13.5) так і при наявності малого лінійного опору (рис.14.2) зсув фаз при резонансному дорівнює π/2.
