Динаміка точки.

§ 1.3. Диференціальні рівняння руху матеріальної точки. Дві задачі динаміки точки.

(Скільки способів завдання руху в “Кінематиці”? відповідь - три)

М

Диференціальні рівняння руху

Векторна

форма

Координатна

форма

Природна (натуральна) форма

аємо три форми диференціальних рівнянь руху (Д.Р.Р.). Розглянемо рух вільної точки масою m, на яку діє система сил { }, к= 1,2...

Згадаємо, що при Осі координат Декартові, При природному

векторному способі тому в “Кінематиці” способі завдання руху

завдання руху точки її задати рух – це задати точки відомі

радіус – вектор функція координати , - траєкторія

ч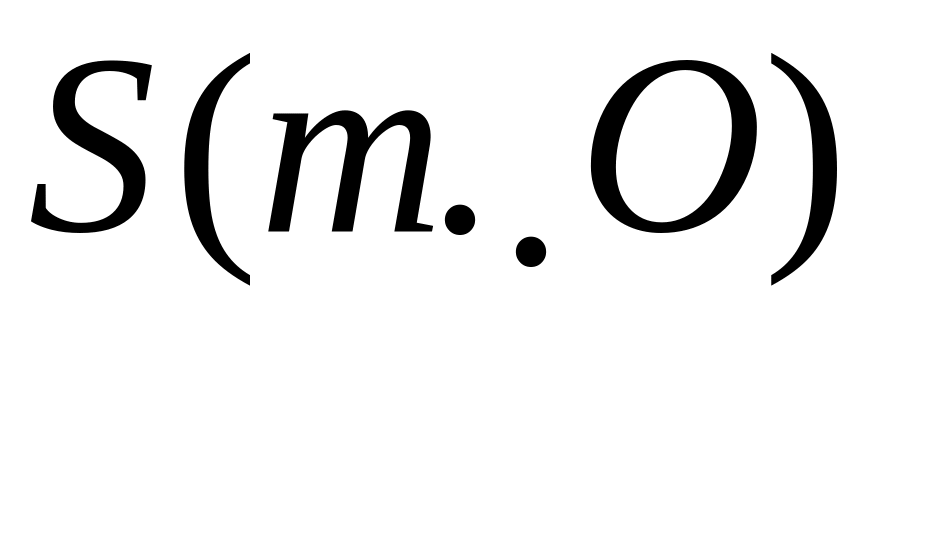 асу , - дугова координата

з початком відрахунку

Для точки з масою Спроціювавши (1.3) на Згадаємо, що осі

рівняння(1.3), осі Ox,Oy,Oz, врахувавши, координат при цьому

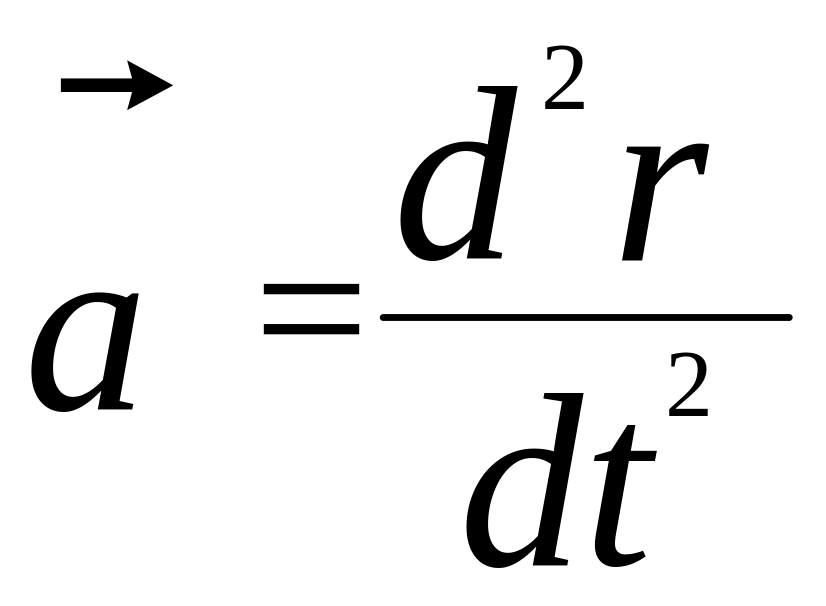враховуючи, що що , , були такі:

маємо: - дотична

- головна нормаль

- бінормаль

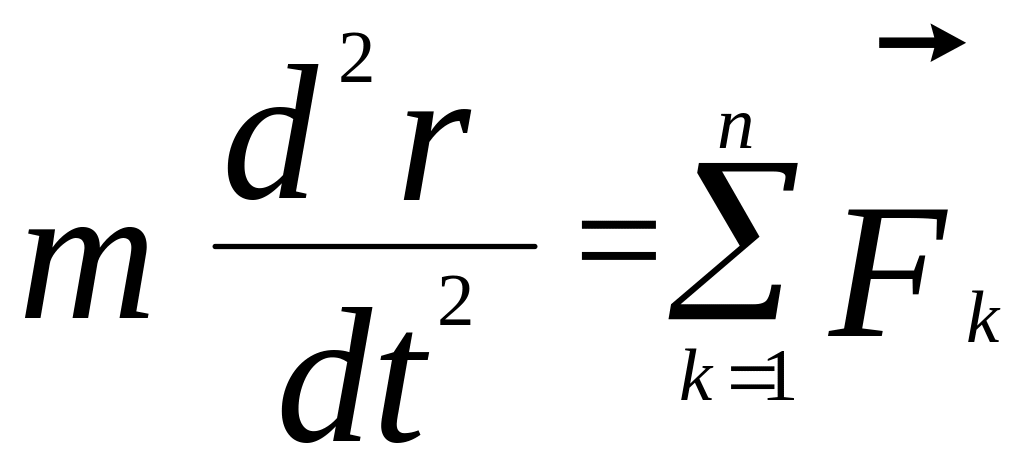
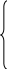
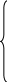
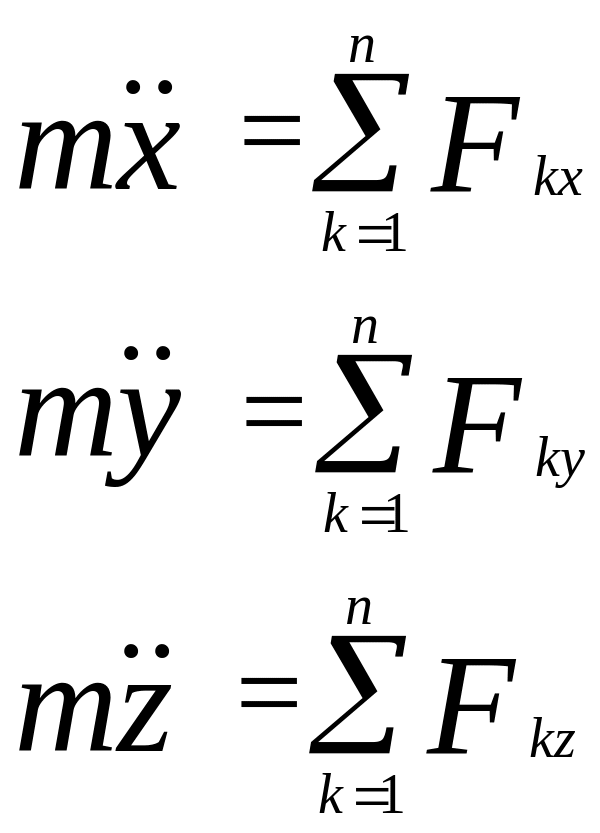
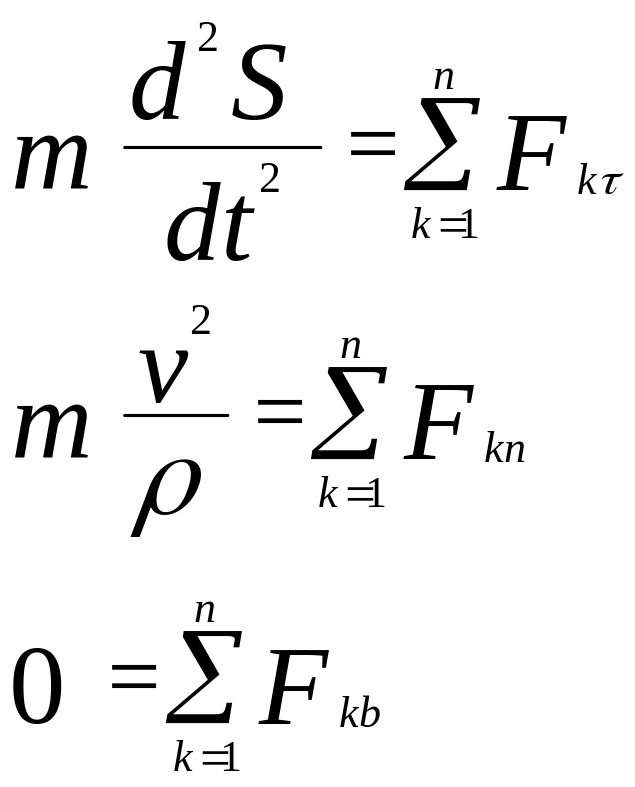
Маючи Д.Р.Р. точки в одному з видів (1.5), (1.6), (1.7) можна розв’язати дві основні задачі динаміки точки.

1. Відомі кінематичні рівняння руху точки заданої маси. Визначити одну з сил, що діє на точку (перша задача динаміки).

2. Відомі сили, що діють на точку в довільний момент часу і маса точки. Визначити кінематичні рівняння руху точки при заданих початкових умовах (друга задача динаміки).

Рекомендації для практичних занять на тему “Друга задача динаміки точки”

Розглянемо, наприклад, рух точки в площині Oxy. Пропонується така послідовність дій.

1. Вибираємо систему відліку (осі координат, t=0) і показуємо точку в довільному положенні.

2. Виходячи з умови задачі, формулюємо початкові умови, тобто записуємо значення проекції початкової швидкості на осі 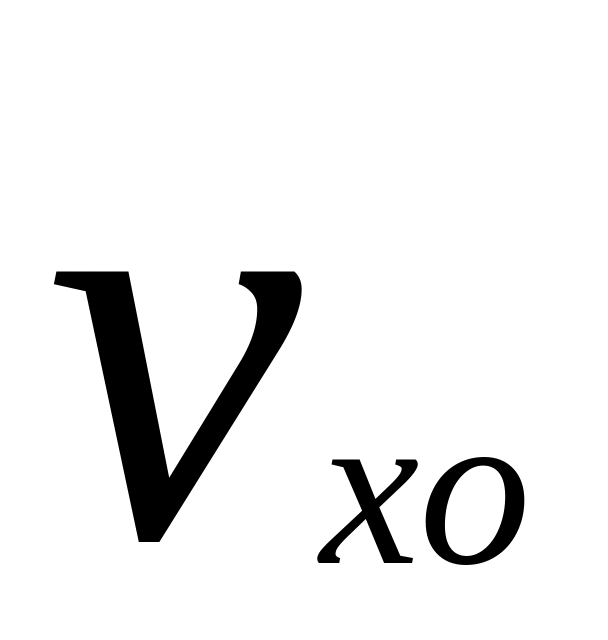, 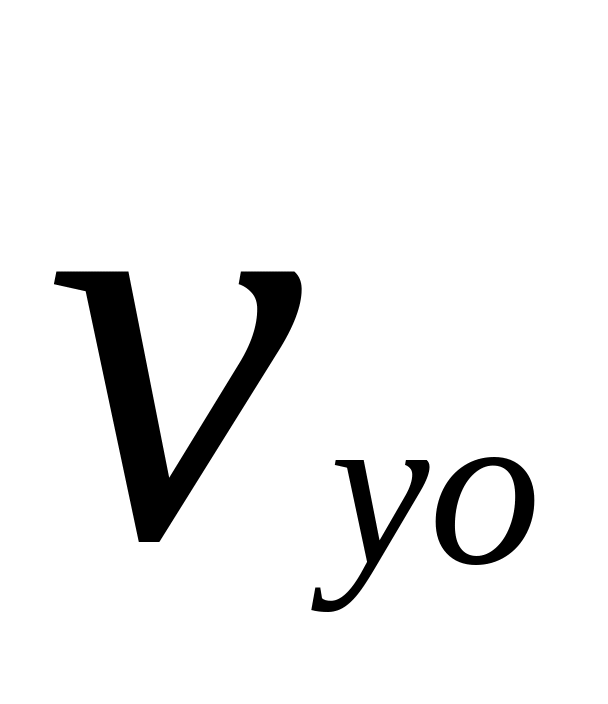та початкові координати x_o, y_o

3. На рисунку показуємо сили, які діють на точку в довільному положенні

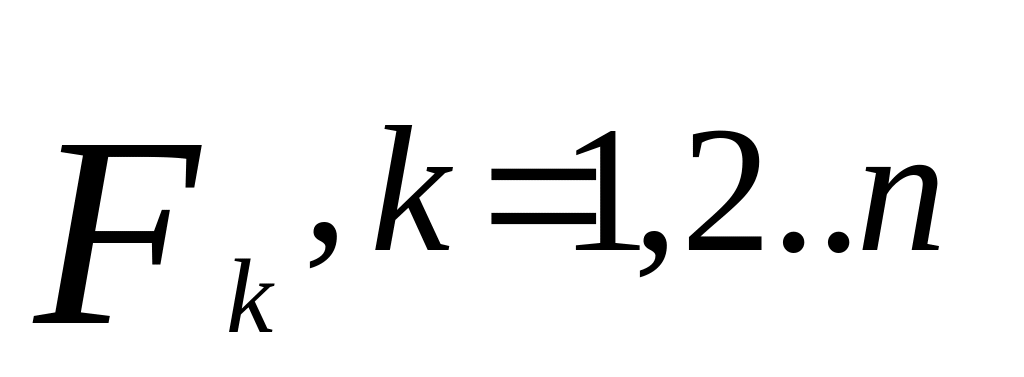
4. С 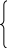кладаємо Д.Р.Р. точки. Для прикладу

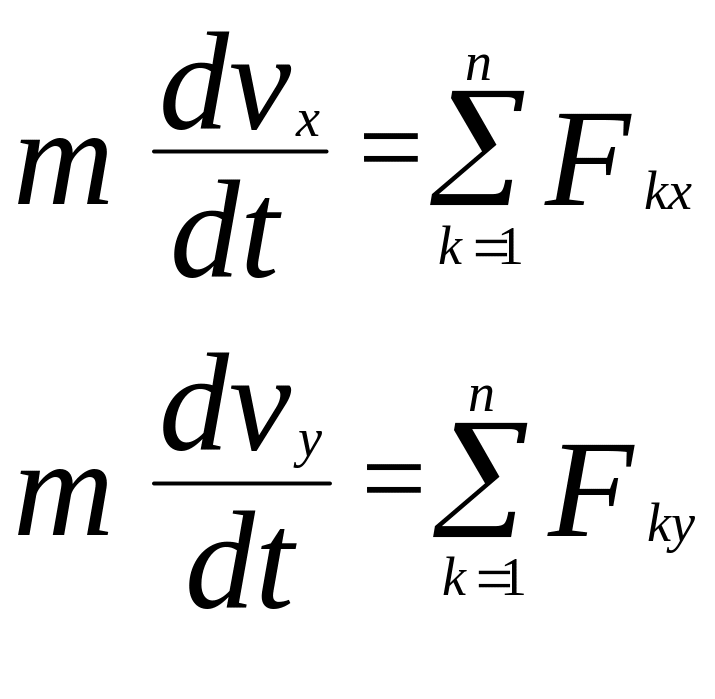
5. Інтегруємо складені диференціальні рівняння; якщо права частина рівняння (тобто сили) постійна, залежить від часу, чи швидкості методом поділу змінних; якщо сила – функція координат, то можна ввести заміну , а потім інтегрувати.

6. При інтегруванні, звичайно, виникають постійні інтегрування; для того щоб їх визначити користуються початковими умовами.

З

Траєкторія руху вільної точки відносно інерціальної системи відліку залежить:

?

?

?

апитання. Від чого залежить траєкторія матеріальної точки по відношенню до інерціальної системи відліку (самостійно)?

Зауваження.

Диференціальні рівняння руху невільної матеріальної точки відрізняються від Д.Р.Р. вільної точки наявністю в правих частинах рівнянь (1.5) ÷ (1.7) реакцій в’язей, які, звичайно, невідомі. Тому на практиці осі координат краще вибирати так, щоб реакції в’язей не проектувалися на ці осі.

Питання для самоконтролю.

1. Запишіть диференціальні рівняння руху матеріальної точки в декартових координатах.

2. Які рівняння називаються диференціальними рівняннями руху точки в натуральній формі?

3. Сформулюйте першу основну задачу динаміки матеріальної точки.

4. Яка сутність другої основної задачі динаміки матеріальної точки?

5. Як визначають постійні інтегрування диференціальних рівнянь руху матеріальної точки?