§ 10.3. Про особливості методу вивчення малих коливань системи.

Повинні виконуватись умови (*):

• н аявність потенціальних сил;

• вивчається рух поблизу положення стійкої рівноваги.

Метод вивчення.

1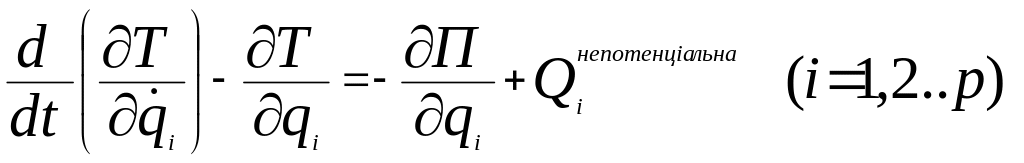 . Для отримання диференціальних рівнянь руху механічної системи будемо використовувати рівняння Лагранжу ІІ роду:

2. Кінетичну і потенціальну енергії системи, які входять в рівняння Лагранжу ІІ роду, будемо брати в наближеному вигляді, бо координати і швидкості – малі величини.

Наприклад, для системи з одним ступенем вільності.

К інетична енергія в положенні рівноваги звичайно дорівнює нулеві. Поблизу положення стійкої рівноваги кінетична енергія системи з одним ступенем вільності дорівнює в випадку стаціонарних в’язей 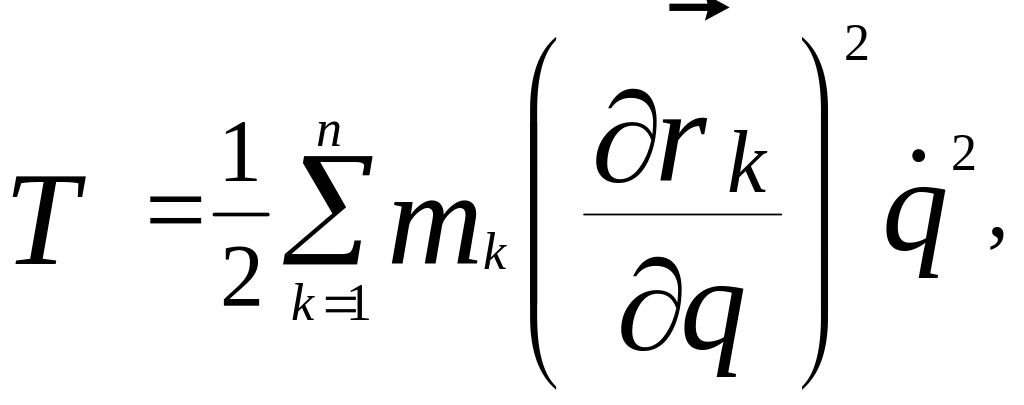, або введемо позначення 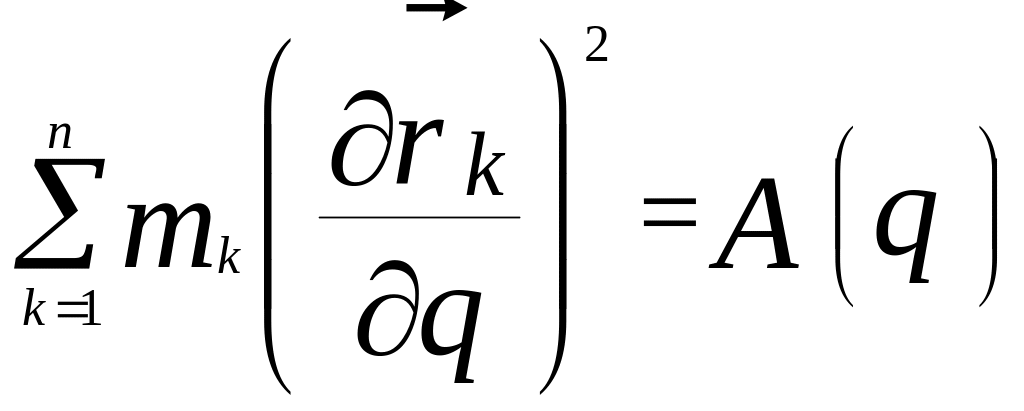– деяка функція узагальненої координати.

Враховуючи те, що , – малі величини, розкладемо в ряд Маклерона поблизу положення рівноваги

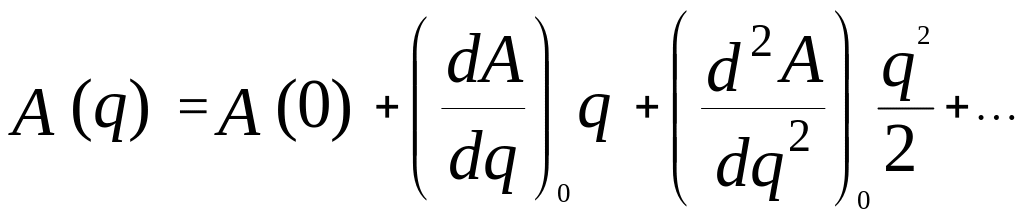
В иявилось, що якщо в виразі (10.4) утримувати члени другого порядку малості, тобто , то ми зможемо проінтегрувати диференціальне рівняння і більша точність непотрібна, бо , – малі. Тобто, якщо позначити А(0)=а – коефіцієнт інерції.

П 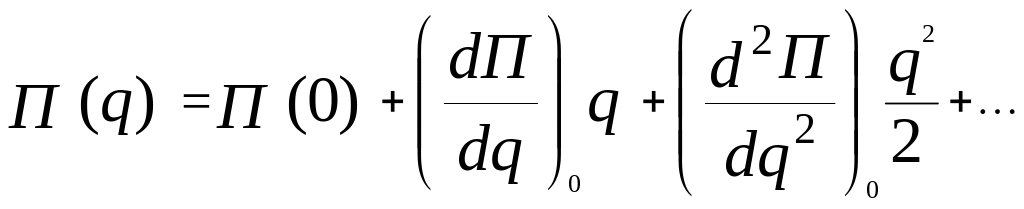отенціальна енергія – це є функція положення, розкладемо її також в ряд Маклерона

В ідомо, що 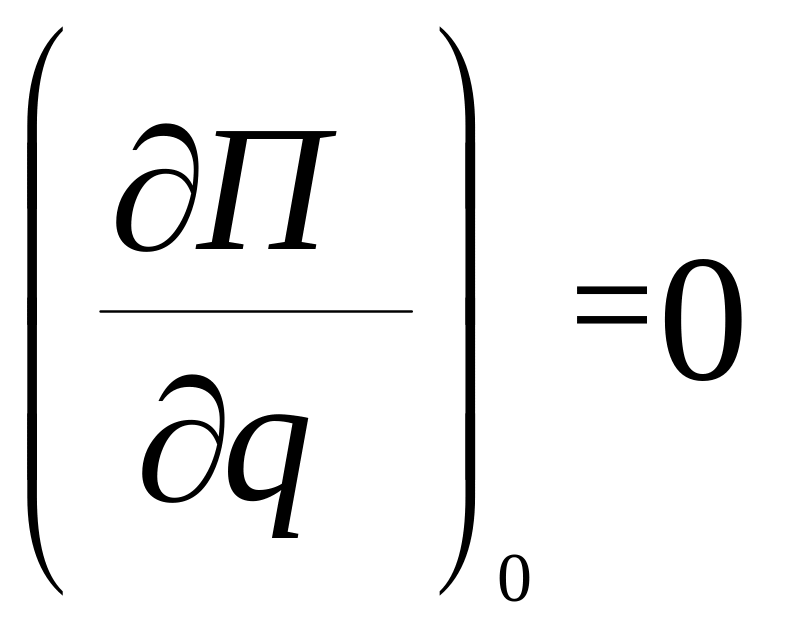(формула (10.1)), постійну П(0) можемо покласти, що вона дорівнює нулеві П(0)=0. Друга похідна від потенціальної енергії в положенні стійкої рівноваги додатна (формула (10.2)). Приймемо, що 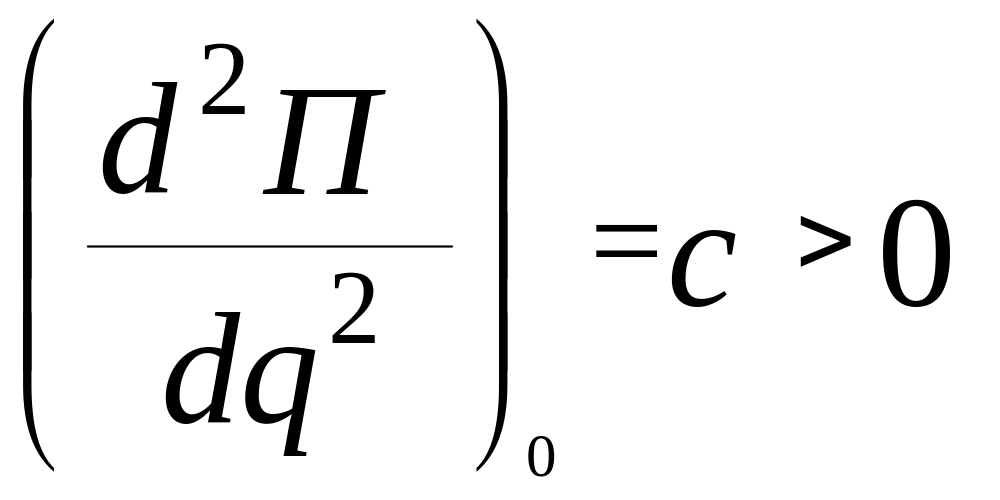, с – коефіцієнт жорсткості.

Т оді (10.6) має вигляд

3. Проінтегрувавши складені диференціальні рівняння, вивчимо властивості руху.

Таким чином маємо алгоритм вивчення малих коливань системи з одним ступенем вільності:

1. Перевірка умов (*);

2. Складання диференціальних рівнянь руху, в яких Т і П в наближеному вигляді (10.5) і (10.7);

3. Інтегрування диференціальних рівнянь (отримання закону руху q=q(t));

4. Дослідження властивостей руху.

Цю послідовність дій будемо виконувати на кожній лекції. Почнемо з найпростіших коливань.

Тема 11. Вільні (власні) коливання механічної системи з одним ступенем вільності.

Література: [2] Гл. 7. §2.

[4] Гл. 11.3.

[3] §6–8.

§ 11.1. Постановка задачі Диференціальне рівняння руху.

Вивчаємо рух механічної системи з одним ступенем вільності з голономними, стаціонарними, ідеальними двосторонніми в’язями. На систему діють тільки потенціальні сили. Положення системи в довільний момент часу визначається узагальненою координатою q, яку відраховуємо від положення стійкої рівноваги.

	Узагальнена координата	Коефіцієнт інерції	Коефіцієнт жорсткості
	q=x, м.	a=m, кг.
	q=φ, рад.	а=IOZ.

Кінетична і потенціальна енергії, згідно з (10.5) і (10.7) мають вигляд , Звичайно розмірність коефіцієнтів а і с залежить від розмірності узагальненої координати.

С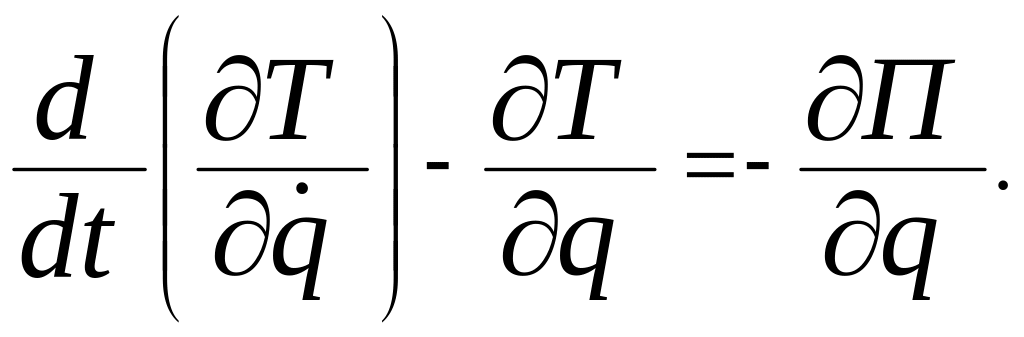 користаємось рівнянням Лагранжу ІІ роду для системи з одним ступенем вільності.

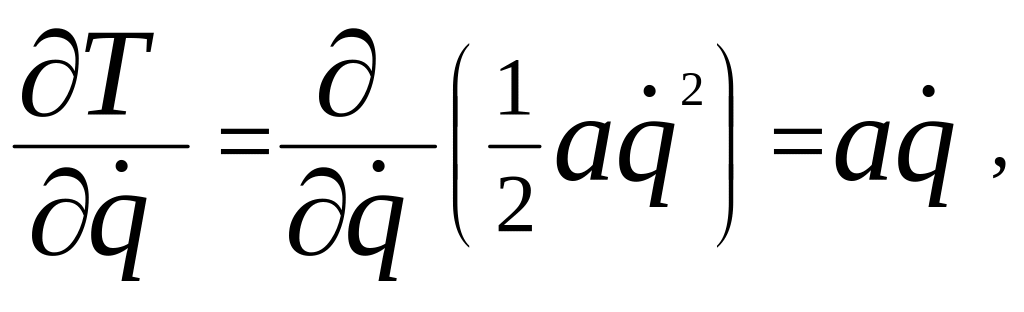
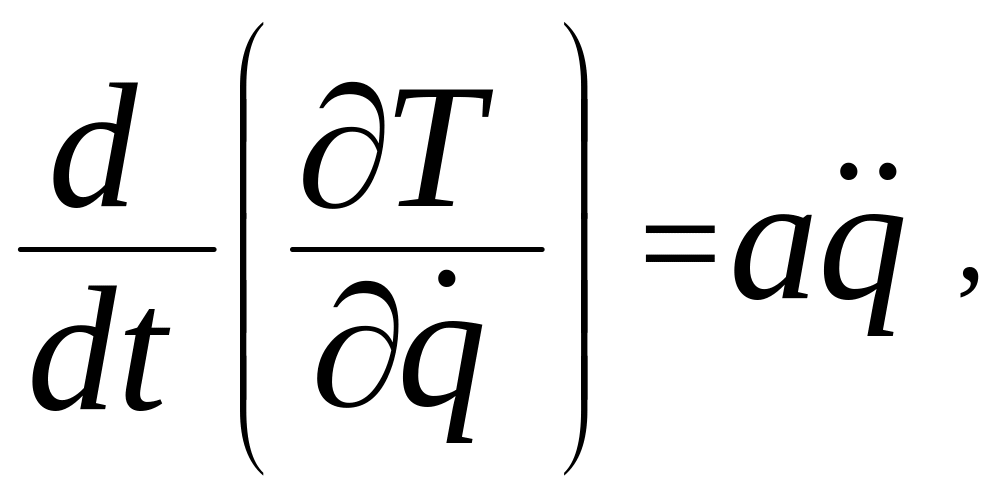
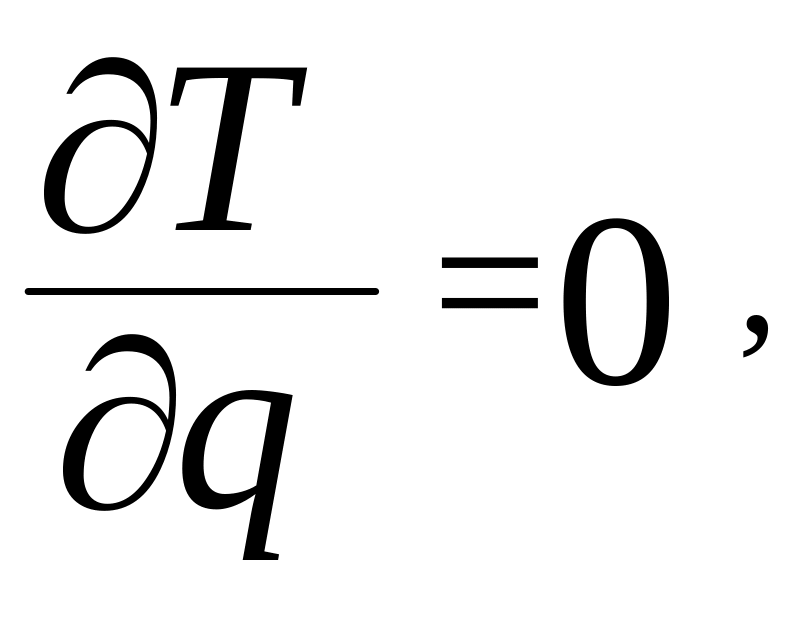
З 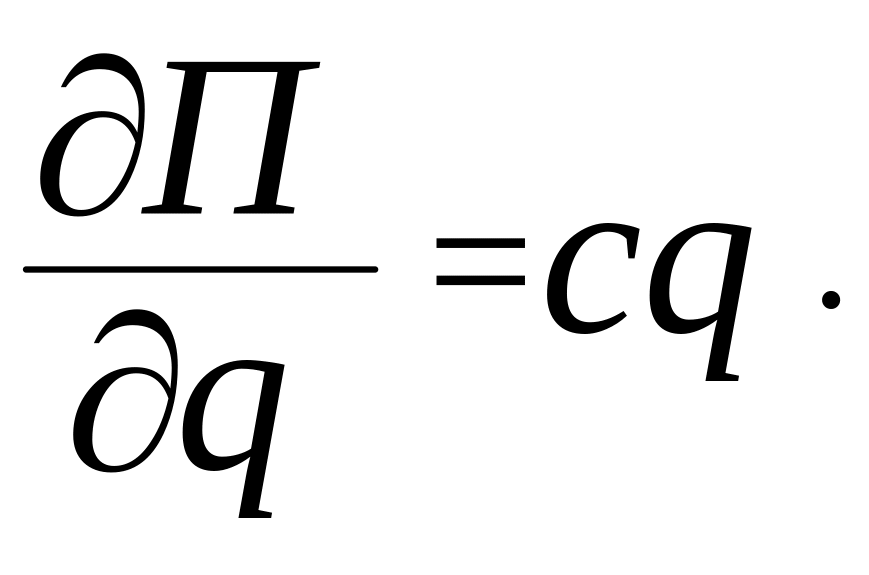найдемо похідні і підставимо їх в рівняння

м аємо

П 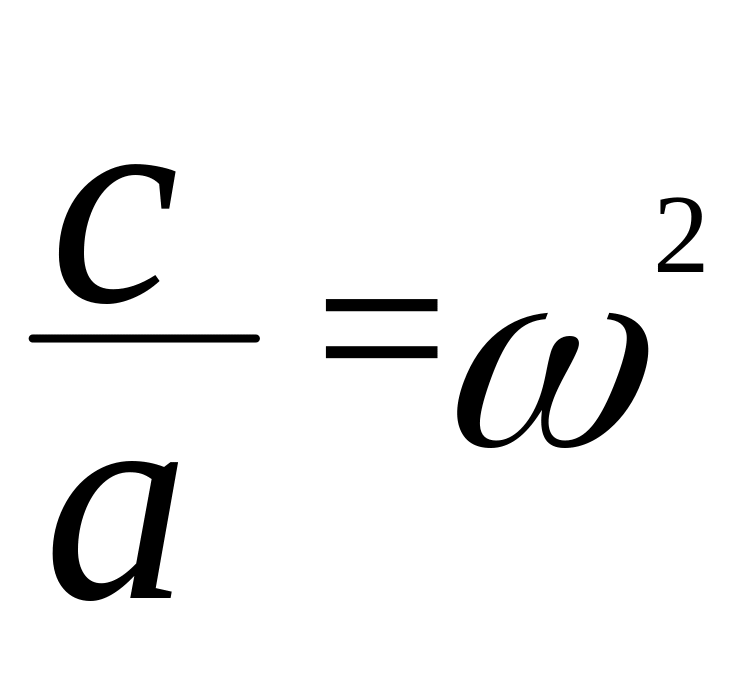оділимо на коефіцієнт інерції і позначимо

Т оді диференціальне рівняння має вигляд

Зверніть увагу, що це - лінійне однорідне диференціальне рівняння ІІ порядку з постійними коефіцієнтами (ЛОДР). Приступимо до його розв’язку.