§ 7.6.2. Для визначення реакцій в’язі складеної конструкції.

Згадаємо, як ми в «Статиці» визначали реакції в'язей конструкції, що складалась з великого числа зв'язаних між собою тіл.

Н априклад. Складена балка з трьох частин.

Скільки рівнянь рівноваги треба скласти для визначення реакцій в'язей в точках А, В, Е та тиск в шарнірах С і D? (Відповідь) – дев'ять. З допомогою принципу можливих переміщень можна визначити одну із реакцій, або її складову вибірково! Тобто визначити, ту реакцію, яка нас «турбує» (потрібна), а не всі.

Як це робиться?

Відкидають ту в'язь, реакцію якої треба визначити. Дію в'язі замінюють її реакцією, яку переводять в клас активних (заданих) сил. При цьому конструкція (яка не мала ступенів вільності – вона нерухома), отримує одну ступінь вільності.

Далі діють так само, як і в § 7.6.1. Тобто

- надають системі можливе переміщення;

- складають рівняння робіт (7.10) (або потужностей (7.11));

- встановлюють зв’язок між можливими переміщеннями (чи швидкостями);

- підставляють знайдені залежності між можливими переміщеннями (чи швидкостями) в рівняння п.м.п. і отримують шукану реакцію.

§ 7.7. Загальне рівняння динаміки, або принцип д’Аламбера – Лагранжа.

Р озглядаємо рух механічної системи, на яку накладені голономні, утримуючі ідеальні в’язі. На кожну точку діють сили: , . Згідно з принципом Д’Аламбера умовно прикладемо до кожної точки силу інерції і отримаємо

Н адамо системі деяке можливе переміщення; кожна точка отримає своє переміщення (к=1,2..n). Скалярна помножимо рівність (а) на і підсумовуючи по всіх точках системи, маємо

З а визначенням ідеальних в’язей середній доданок дорівнює нулеві (формула (7.9)). Маємо принцип Д’Аламбера – Лагранжа

Принцип Д’Аламбера – Лагранжа. В довільний момент руху механічної системи з ідеальними в’язями сума можливих робіт активних сил та сил інерції точок системи на будь-якому можливому переміщенні системи дорівнює нулеві.

Рівняння (7.12) ще називають загальним рівнянням динаміки і складають їх стільки, скільки ступенів вільності. Для системи з голономними, двосторонніми, ідеальними в’язями з рівнянням (7.12) можна отримати загальні теореми динаміки, динамічні рівняння руху, тобто побувати теоретичний курс розділу “Динаміка”.

Рекомендації до практичних занять на тему:

„Застосування загального рівняння динаміки для складання динамічного рівняння руху практичної моделі механічної системи”.

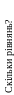
П окажемо послідовність дій з допомогою схеми.

Якщо серед в’язей є неідеальні в’язі, то їх реакції “переводять” в клас активних сил.

Питання для самоконтролю.

1. Що називається в’яззю?

2. Яке загальне рівняння в’язі?

3. Яка в’язь називається утримуючою?

4. Яка в’язь називається стаціонарною?

5. Які в’язі називаються голономними?

6. Що називають можливим переміщенням механічної системи?

7. Чи залежать можливі переміщення від діючих на систему сил?

8. Яка відмінність між можливим і дійсним переміщенням системи?

9. В якому випадку дійсне переміщення системи співпадає з одним з її можливих переміщень?

10. Що називається числом ступенів вільності системи?

11. Чому дорівнює число ступенів вільності системи, на яку накладені тільки голономні в’язі?

12. Які в’язі називаються ідеальними?

13. Поясніть, чому ідеально гладка поверхня є ідеальною в’яззю?

14. Чи може бути ідеальною в’язь з тертям?

15. Як формулюється принцип можливих переміщень?

16. Чи можна застосовувати принцип можливих переміщень для дослідження рівноваги механічних систем з неідеальними в’язями?

17. Як формулюється принцип Д’Аламбера – Лагранжа?