
- •З Стор. Міст.
- •Тема 1. Вступ в розділ «Динаміка». Динаміка точки
- •§ 1.1. Предмет і задачі розділу “Динаміка”
- •§ 1.2. Закони класичної механіки.
- •1 Закон (інерції)
- •3 Закон (дії протидії)
- •2 Закон (основний)
- •Динаміка точки.
- •§ 1.3. Диференціальні рівняння руху матеріальної точки. Дві задачі динаміки точки.
- •Рекомендації для практичних занять на тему “Друга задача динаміки точки”
- •Питання для самоконтролю.
- •Динаміка механічної системи.
- •Тема 2. Вступ до “Динаміки механічної системи”.
- •§ 2.1. Структурні та інерційні характеристики механічної системи.
- •Н айменший осьовий момент інерції тіла відносно осі, яка проходить через центр мас.
- •§ 2.2. Осьові моменти інерції деяких твердих однорідних тіл, масою m.
- •§ 2.3. Класифікація сил, їх властивості.
- •§ 2.4. Динамічні рівняння руху системи (для теоретичної моделі).
- •Або в проекціях на осі координат
- •Питання для самоконтролю.
- •Розділ “Загальні теореми динаміки”.
- •Тема 3. Перша загальна теорема динаміки: про зміну кількості руху, або про рух центру мас системи.
- •§ 3.1. Кількість руху точки, системи.
- •§3.2 Теорема про зміну кількості руху (теорема імпульсів).
- •§ 3.3 Закон збереження кількості руху механічної системи ( частинний випадок теореми).
- •Питання для самоконтролю.
- •Тема 4. Теорема про зміну кінетичного моменту. Динамічні рівняння руху твердих тіл.
- •§4.1 Кінетичний момент матеріальної точки та механічної системи.
- •§4.1.1 Кінетичний момент відносно центру.
- •§4.1.2. Кінетичний момент відносно осі.
- •П роекція кінетичного моменту матеріальної точки відносно деякого центру на вісь, яка проходить через цей центр, дорівнює кінетичному моментові точки відносно цієї осі.
- •§4.2. Кінетичний момент тіла відносно осі обертання.
- •§4.3. Теорема про зміну кінетичного моменту.
- •§ 4.4. Диференціальні рівняння простих рухів.
- •§4.5. Динамічні рівняння плоско–паралельного руху твердого тіла.
- •§4.5.1. Теорема про зміну кінетичного моменту механічної системи при відносному русі.
- •§4.5.2. Динамічні рівняння плоского руху.
- •§ 4.6. Наслідки теорем. Закони збереження кінетичних моментів.
- •Рекомендації для практичних занять на тему
- •Питання для самоконтролю.
- •Тема 5. Теорема про зміну кінетичної енергії механічної системи.
- •§ 5.1. Робота і потужність сили та пари сил.
- •§5.2. Приклади обчислення робіт.
- •§5.2.1. Робота сили тяжіння (сили ваги).
- •§5.2.2. Робота сили пружності.
- •§5.2.3. Робота постійної сили.
- •§5.3. Кінетична енергія.
- •§5.3.1. Теорема Кьоніга про кінетичну енергію.
- •§5.3.2. Кінетична енергія твердих тіл.
- •§5.4. Теорема про зміну кінетичної енергії.
- •§5.4.1. Теорема в випадку незмінюваної механічної системи.
- •§5.4.2. Теорема в випадку системи з ідеальними в’язями.
- •§5.5. Інтегральна форма теореми про зміну кінетичної енергії системи.
- •§5.6. Теорема про зміну кінетичної енергії в випадку потенціального силового поля.
- •Рекомендації до практичних занять на тему “ Теорема про зміну кінетичної енергії”.
- •Питання для самоконтролю.
- •Розділ Принципи механіки.
- •Тема 6. Принцип д`Аламбера (умовного зрівноваження сил).
- •§6.1. Принцип д`Аламбера для матеріальної точки.
- •§6.2. Принцип д`Аламбера для механічної системи
- •§6.3. Головний вектор і головний момент сил інерції.
- •§6.4. Головні вектори та головні моменти д’Аламберових сил інерції твердих тіл. (законспектувати самостійно).
- •Рекомендації по застосуванню принципу д’Аламбера (методу кінетостатики)
- •Питання для самоконтролю.
- •Тема 7. Принцип можливих переміщень. Загальне рівняння динаміки.
- •§ 7.1. Класифікація в’язей.
- •§ 7.2. Можливі переміщення.
- •§ 7.3. Число ступенів вільності.
- •§ 7.4. Можлива робота. Ідеальні в’язі.
- •§ 7.5. Принцип можливих переміщень.
- •§ 7.6. Застосування принципу можливих переміщень.
- •§ 7.6.1 Для визначення однієї з активних сил, що діють на систему з одним ступенем вільності.
- •§ 7.6.2. Для визначення реакцій в’язі складеної конструкції.
- •§ 7.7. Загальне рівняння динаміки, або принцип д’Аламбера – Лагранжа.
- •Рекомендації до практичних занять на тему:
- •Питання для самоконтролю.
- •Тема 8. Аналітична механіка в узагальнених координатах.
- •§ 8.1. Узагальнені координати.
- •§ 8.2. Узагальнені сили.
- •§ 8.2.1. Практичний спосіб обчислення - “j”-ої узагальненої сили.
- •§ 8.2.2. Обчислення узагальненої потенціальної сили.
- •§ 8.3. Принцип можливих переміщень в узагальнених координатах.
- •§ 8.4. Загальне рівняння динаміки в узагальнених координатах, або рівняння Лагранжу іі роду.
- •§ 8.5. Рівняння Лагранжу іі роду для консервативних систем.
- •§ 8.6. Застосування рівнянь Лагранжу іі роду для складання диференціальних рівнянь руху практичної моделі механічної системи.
- •Питання для самоконтролю.
- •Тема 9. Динамічне рівняння руху машини.
- •§ 9.2. Зведення сил.
- •§ 9.3. Складання динамічного рівняння руху машини.
- •Розділ. Малі лінійні коливання механічної системи.
- •Тема 10. Вступ в теорію малих лінійних коливань.
- •§ 10.1. Види механічних коливань.
- •§ 10.2. Поняття про стійкість рівноваги. Теорема Лагранжа – Діріхле.
- •§ 10.3. Про особливості методу вивчення малих коливань системи.
- •Метод вивчення.
- •Тема 11. Вільні (власні) коливання механічної системи з одним ступенем вільності.
- •§ 11.1. Постановка задачі Диференціальне рівняння руху.
- •§ 11.2. Закон малих власних вільних коливань.
- •§ 11.3. Властивості руху.
- •Основні властивості власних коливань.
- •Тема 12. Вплив лінійного опору на лінійні власні коливання системи з одним ступенем вільності.
- •§ 12.1. Узагальнена сила опору. Функція Релея.
- •§ 12.2. Постановка задачі. Диференціальне рівняння руху.
- •§ 12.3. Інтегрування диференціального рівняння руху.
- •§ 12.4. Властивості руху при малому опорі.
- •§ 12.5. Аперіодичний рух
- •Тема 13. Вимушені коливання механічної системи з одним ступенем вільності (без врахування опору).
- •§ 13.1. Постановка задачі.
- •§ 13.2. Диференціальне рівняння вимушених коливань.
- •§ 13.3. Рівняння (закон) руху.
- •§ 13.4. Властивості вимушених коливань.
- •§ 13.5. Випадок резонансу.
- •Тема 14. Вимушені коливання механічної системи з одним ступенем вільності з врахуванням лінійного опору.
- •§ 14.1. Постановка задачі.
- •§ 14.2. Інтегрування диференціального рівняння руху. Закон руху.
- •§ 14.3. Властивості вимушених коливань.
- •§ 14.4. Залежність амплітуди та фази вимушених коливань від частоти та фази збурюючої сили.
- •Висновки.
- •Питання для самоконтролю.
§ 7.5. Принцип можливих переміщень.
Сучасне формулювання принципу можливих переміщень було дане Лагранжем в 1788 році в результаті узагальнення теорії найпростіших механізмів (важеля, похилої площини, блоків і т.п.). Тому його називають принципом Лагранжа. Цей вчений, написав книгу “Аналітична механіка”, в якій немає ні одного рисунка. Він писав: “Всі, хто любить математику з задоволенням дізнаються, що механіка – галузь математики”.
П![]()
![]() ринцип
Лагранжа: Для рівноваги механічної
системи з геометричними двосторонніми,
ідеальними, стаціонарними в’язями
необхідно і достатньо, щоб алгебраїчна
сума можливих робіт всіх активних сил,
що діють на систему, на будь-якому з її
можливих переміщень дорівнювала нулеві,
тобто
ринцип
Лагранжа: Для рівноваги механічної
системи з геометричними двосторонніми,
ідеальними, стаціонарними в’язями
необхідно і достатньо, щоб алгебраїчна
сума можливих робіт всіх активних сил,
що діють на систему, на будь-якому з її
можливих переміщень дорівнювала нулеві,
тобто
Необхідність. Нехай механічна система, що складається з “n” матеріальних точок, знаходиться в рівновазі і на неї накладені геометричні, утримуючі, ідеальні, стаціонарні в’язі. Позначимо:
![]() - рівнодійна активних сил, що діють на
„к”-ту точку,
- рівнодійна активних сил, що діють на
„к”-ту точку,
![]() - рівнодійна реакцій в’язей, що діють
на „к”-ту точку.
- рівнодійна реакцій в’язей, що діють
на „к”-ту точку.
О![]()
![]() скільки
система знаходиться в рівновазі, то
кожна її точка також у рівновазі, а
значить
скільки
система знаходиться в рівновазі, то
кожна її точка також у рівновазі, а
значить
Н
![]()
![]() адамо
системі одне з можливих переміщень і
позначимо переміщення “к”-ої точки -
. Помножимо скалярна на
кожну рівність (*).
адамо
системі одне з можливих переміщень і
позначимо переміщення “к”-ої точки -
. Помножимо скалярна на
кожну рівність (*).
Д![]()
![]() одамо
“n” рядків (**)
одамо
“n” рядків (**)
В![]()
![]() раховуючи,
що в’язі ідеальні, тобто має місце
(7.9), в рівнянні (***) залишиться тільки
перша сума
раховуючи,
що в’язі ідеальні, тобто має місце
(7.9), в рівнянні (***) залишиться тільки
перша сума
що і треба було довести.
Достатність (самостійно довести).
Увага! Рівнянь робіт (7.10) можна скласти стільки, скільки незалежних можливих переміщень, тобто скільки ступенів вільності має механічна система.
До речі, згадайте з курсу „Фізика” золоте правило механіки. Не впізнаєте його в (7.10’)?
§ 7.6. Застосування принципу можливих переміщень.
§ 7.6.1 Для визначення однієї з активних сил, що діють на систему з одним ступенем вільності.
Пропонується послідовність дій, проілюстрована для конкретної задачі.
З




![]()
![]()
![]()
![]() адача.
Визначити, який момент треба прикласти
до кривошипа 1 в кривошипно-шатунному
механізмі щоб зрівноважити силу
, прикладену до поршня 3. (Рис. 7.1) при
заданому кутові
. Механізм розташований в горизонтальній
площині, в’язі ідеальні. ОА та АВ –
відомі.
адача.
Визначити, який момент треба прикласти
до кривошипа 1 в кривошипно-шатунному
механізмі щоб зрівноважити силу
, прикладену до поршня 3. (Рис. 7.1) при
заданому кутові
. Механізм розташований в горизонтальній
площині, в’язі ідеальні. ОА та АВ –
відомі.
1) Вибираємо об’єкт вивчення. |
1) Об’єкт вивчення – механічна система, що складається з тіл: 1, 2, 3. |
2) З'ясовуємо вид в'язей та число ступенів вільності. Щоб з'ясувати число ступенів вільності для плоских механізмів: - зупиняємо одну ланку; - з'ясовуємо, чи всі ланки "зупинились"? - якщо всі – один ступінь вільності. |
2) В'язі – геометричні, стаціонарні, ідеальні. Система має одну ступінь вільності. (Якщо "зупинити" кривошип 1, всі точки механізму зупиняться). |
3) Показуємо на рисунку активні сили, які діють на систему. |
3) Активні сили: пара сил з моментом М та сила (сили ваги ланок перпендикулярні до площини рисунка). |
4) Надаємо системі можливе переміщення і складаємо рівняння (7.10). |
4) Надаємо кривошипові 1 можливе
переміщення проти ходу годинникової
стрілки. Рівняння (7.10) має вигляд
|
5) Для системи з одним ступенем вільності отримуємо залежності між можливими переміщеннями. До речі, ці залежності такі самі, як і для можливих швидкостей. Тому рівняння робіт (7.10') можна замінити рівнянням потужностей
де
|
При заданих
геометричних параметрах ОА,
,АВ відношення переміщень
|
6) Підставляємо залежності між можливими переміщеннями (або швидкостями) в рівняння (7.10') або (7.11) і враховуючи, що задане можливе переміщення довільне, отримуємо шукану силу, чи момент. |
6)
|

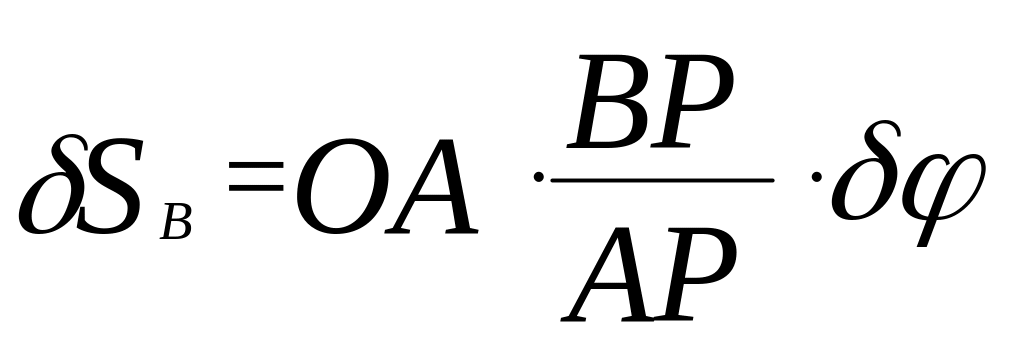 5)
Залежність між можливими переміщеннями
отримали раніше (див. рис.7.1)
5)
Залежність між можливими переміщеннями
отримали раніше (див. рис.7.1)
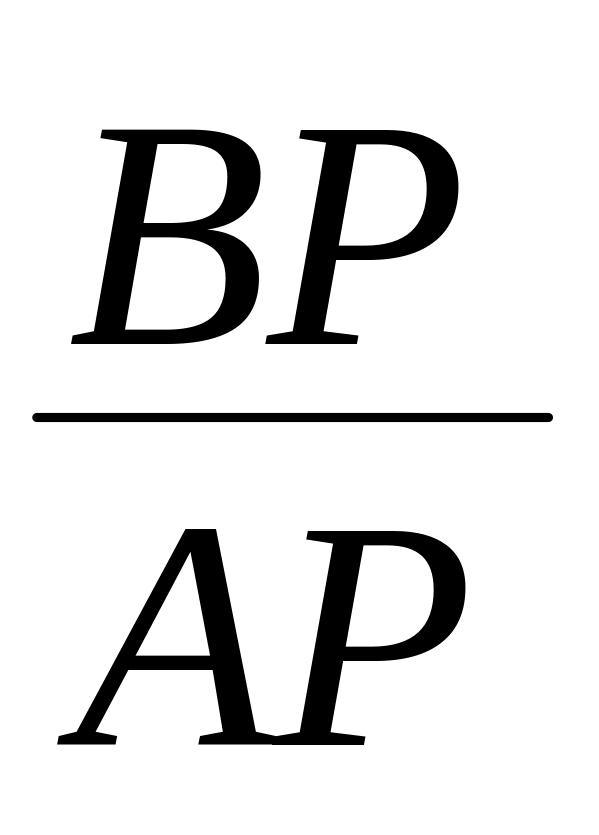 легко отримати розглядаючи трикутники
АВР, ОВР, та АОВ.
легко отримати розглядаючи трикутники
АВР, ОВР, та АОВ.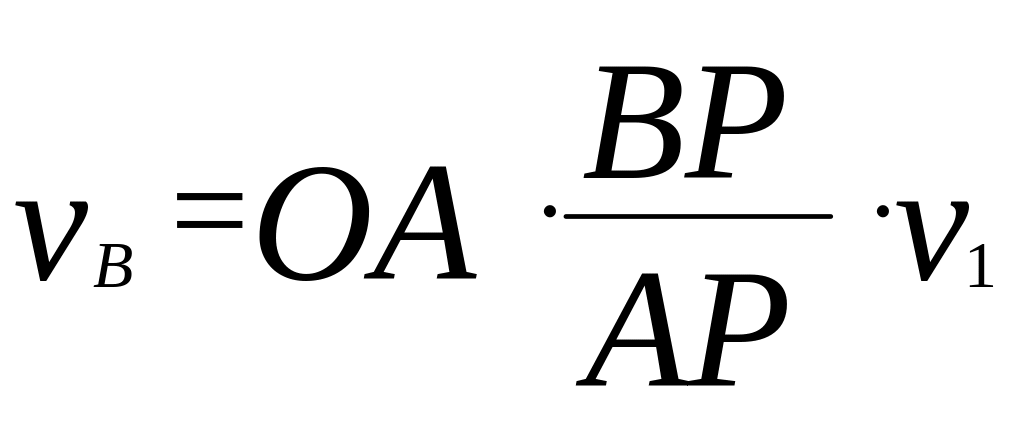 Така
ж сама залежність між швидкостями
Така
ж сама залежність між швидкостями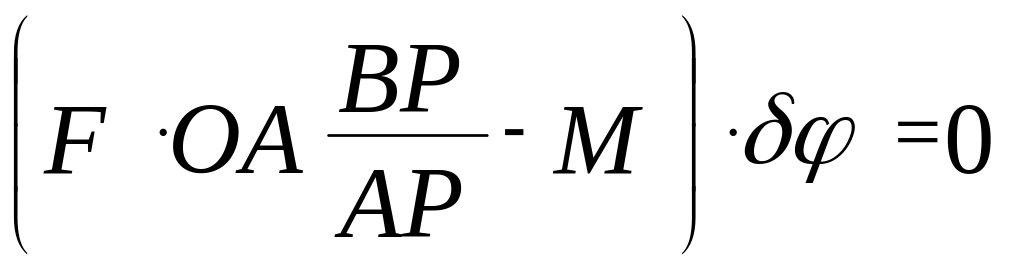 ,
,
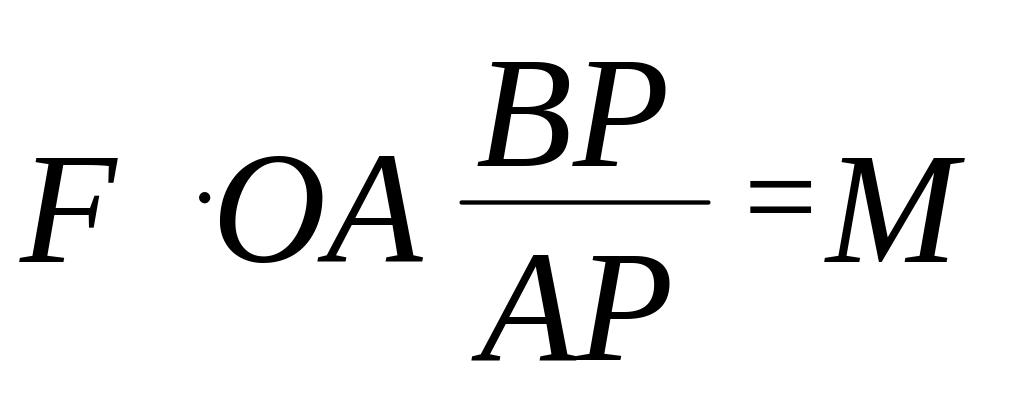 отримали шуканий момент М.
отримали шуканий момент М.