Хід роботи:

Найпростіший тест простоти полягає в такому: коли задане число n, перевірити чи якесь ціле m від 2 до n-1 ділить n. Якщо n ділиться на певне m, то n складене, в іншому разі воно просте. Замість перевірки всіх m до n-1, досить лише перевірити m до  : якщо n складене, то його можна розкласти на два множники, принаймні один з яких не перевищує  . Можна також покращити ефективність, пропускаючи всі парні m , за винятком 2, бо коли якесь парне число ділить n , то 2 також ділить. Визначимо які числа необхідно дослідити не те чи вони прості чи складенні.

4(mod 7) + 1 ≡ 5

Для побудованого варіанту спіралі це числа: 139; 144; 149; 154; 159; 164; 169; 174.

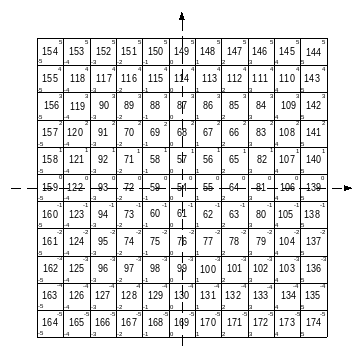Перевіримо число 139:

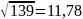
Отже знайдемо НСД числа 139 і чисел 2, 3, 5, 7, 9, 11.

НСД (139,2):

139 = 69*2 + 1;

2 = 1*2 + 0

Отже 139 і 2 не мають спільних дільників окрім 1.

НСД(139,3):

139 = 46*3 + 1;

3 = 3*1 + 0

Отже 139 і 3 не мають спільних дільників окрім 1.

НСД(139,5)

139 = 27*5 + 4;

5 = 1*4 + 1;

4 = 4*1 + 0

Отже 139 і 5 не мають спільних дільників окрім 1.

НСД(139,7)

139 = 19*7 + 6;

7 = 6*1 + 1;

6 = 1*6 + 0

Отже 139 і 7 не мають спільних дільників окрім 1.

НСД(139,9)

139 = 15*9 + 4;

9 = 2*4 + 1;

4 = 4*1 + 0

Отже 139 і 9 не мають спільних дільників окрім 1.

НСД(139,11)

139 = 12*11 + 7;

11 = 1*7 + 4;

7 = 1*4 + 3;

4 = 1*3 + 1;

3 = 3*1 + 1

Отже 139 і 11 не мають спільних дільників окрім 1. Проаналізувавши результати можна сказати що число 139 просте. Перевіримо число 144:

Отже знайдемо НСД числа 144 і чисел 2, 3, 5, 7, 9, 11, 12.

НСД(144,12)

144 = 12*12+0

Отже число 144 є складеним і його можна розкласти на такі множники:

144 =12*3*2*2

Знаючи властивості простих чисел в подальшому будь – яке парне число окрім двійки зразу відноситимемо до складених чисел. Отже числа 154, 164, 174 є складеними. Перевіримо число 149:

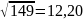
Отже знайдемо НСД числа 149 і чисел 2, 3, 5, 7, 9, 11.

НСД(149,2)

149 = 74*2 + 1;

2 = 2*1 + 0

Отже 149 і 2 не мають спільних дільників окрім 1.

НСД(149,3)

149 = 49*3 + 2;

3 = 1*2 + 1;

2 = 2*1 + 0

Отже 149 і 3 не мають спільних дільників окрім 1.

НСД(149,5)

149 = 29*5 + 4;

5 = 4*1 + 1;

4 = 4*1 + 1;

1 = 1*1 + 0

Отже 149 і 5 не мають спільних дільників окрім 1.

НСД(149,7)

149 = 21*7 + 2;

7 = 3*2 + 1;

2 = 2*1 + 0

Отже 149 і 7 не мають спільних дільників окрім 1.

НСД(149,9)

149 = 16*9 + 5;

9 = 1*5 + 4;

5 = 1*4 + 1;

4 = 4*1 + 0

Отже 149 і 9 не мають спільних дільників окрім 1.

НСД(149,11)

149 = 13*11 + 6;

11 = 1*6 + 5;

6 = 1*5 + 1;

5 = 5*1 + 0

Отже 149 і 11 не мають спільних дільників окрім 1. Проаналізувавши результати можна сказати що число 149 просте. Перевіримо число 159:

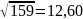
НСД(159,2)

159 = 79*2 + 1;

2 = 2*1 + 0

Отже 159 і 2 не мають спільних дільників окрім 1.

НСД(159,3)

159 = 53*3 – отже число складене. Перевіримо число 169:

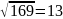
НСД(169,13)

163 = 13*13 + 0 – отже число складене.

Приклад №11

Хід роботи:

Встановити чи число на вертикалях, горизонталях, двох головних піддіагоналях та двох бічних піддіагоналях з порядковим номером k 67 (mod 7)+1 є просте, чи складене для числової спіралі з центром 67.