Міністерство освіти і науки, молоді та спорту України

Національний університет «Львівська політехніка»

Інститут комп’ютерних наук та інформаційних технологій

Кафедра автоматизованих систем управління

Лабораторна роботи №2

на тему:

«Встановлення властивостей натуральних чисел»

Львів 2013

Лабораторна робота № 2

Тема: Встановлення властивостей натуральних чисел

Мета: Навчитись встановлювати властивості заданих натуральних чисел

Короткі теоретичні відомості

Додатні числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ..., що з’явилися в результаті рахунку називаються натуральними і утворюють натуральний ряд чисел. Для запису натуральних чисел користуються десятковою системою числення, в основі якої лежать десять знаків - цифр. На першому місці в натуральному ряді стоїть число 1, за ним іде число 2, далі 3 і так до 9. Після 9, згідно з правилом десяткового числення, йде число 10, а за 10 іде 11, і у натуральному ряді немає останнього числа - за кожним натуральним числом стоїть ще одне натуральне число, за яким - ще одне і т.д.

Натуральних чисел нескінченно багато. Найбільше натуральне число назвати в принципі неможливо, оскільки нескінченність ряду таких чисел розуміє обов'язкову наявність числа, більшого будь-якого названого на 1. За цих умов правий край ряду натуральних чисел прийнято позначати символом нескінченності (значок ∞).

Крім того, всяке натуральне число відноситься або до класу простих чисел, або до класу складених чисел; відповідно, ряд натуральних чисел складається з простих і складених чисел. Просте число ділиться без залишку тільки на себе і на 1, тому має лише два позитивних дільники. Натуральне число, яке ділиться без залишку ще на якесь натуральне число, крім самого себе і 1 називається складеним.

Найпростіший тест простоти полягає в такому: коли задане число n, перевірити чи якесь ціле m від 2 до n-1 ділить n. Якщо n ділиться на певне m, то n складене, в іншому разі воно просте. Замість перевірки всіх m до n-1, досить лише перевірити m до : якщо n складене, то його можна розкласти на два множники, принаймні один з яких не перевищує :. Можна також покращити ефективність, пропускаючи всі парні m , за винятком 2, бо коли якесь парне число ділить n , то 2 також ділить. Можна далі вдосконалити зауважуючи, що всі прості числа, за винятком 2 та 3, мають вигляд 6k ± 1. Дійсно, всі цілі можна подати як (6k + i) для деякого k та для i = -1, 0, 1, 2, 3, або 4; 2 ділить (6k + 0), (6k + 2), (6k + 4); а 3 ділить (6k + 3). Спочатку перевіряємо чи n ділиться на 2 або 3, тоді пробігаємо всі числа вигляду 6k ± 1 . 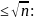Це у 3 рази швидше від попереднього методу. Насправді, всі прості мають вигляд c^* k + i lkz i<c^* де i належить до чисел, взаємно простих з c^*. Фактично, коли c->∞ кількість значень, які c^* k + i може набувати в певному діапазоні, зменшується, а, отже, час тестування n зменшується. Для цього методу, слід ділити на всі прості менші ніж c. Спостереження, аналогічні до попереднього, можна застосувати рекурсивно, отримуючи сито Ератосфена. Вдалим способом пришвидшення цих методів (і всіх інших згаданих далі) є попередній обрахунок і зберігання списку всіх простих до певної межі, скажімо всіх простих до 200. (Такий список можна обчислити за допомогою сита Ератосфена). Тоді, перед тестуванням n на простоту з використанням серйозного методу, спочатку перевіряємо чи n не ділиться на якесь просте із цього списку.

Для перевірки чисел та знаходження того, що воно є просте чи складне існують такі методи:

Наївні методи

Найпростіший тест простоти полягає в такому: коли задане число n, перевірити чи якесь ціле m від 2 до n-1 ділить n. Якщо n ділиться на певне m, то n складене, в іншому разі воно просте. Замість перевірки всіх m до n-1, досить лише перевірити m до : якщо n складене, то його можна розкласти на два множники, принаймні один з яких не перевищує :. Можна також покращити ефективність, пропускаючи всі парні m , за винятком 2, бо коли якесь парне число ділить n , то 2 також ділить. Можна далі вдосконалити зауважуючи, що всі прості числа, за винятком 2 та 3, мають вигляд 6k ± 1. Дійсно, всі цілі можна подати як (6k + i) для деякого k та для i = -1, 0, 1, 2, 3, або 4; 2 ділить (6k + 0), (6k + 2), (6k + 4); а 3 ділить (6k + 3). Спочатку перевіряємо чи n ділиться на 2 або 3, тоді пробігаємо всі числа вигляду 6k ± 1 . Це у 3 рази швидше від попереднього методу. Насправді, всі прості мають вигляд c^* k + i lkz i<c^* де i належить до чисел, взаємно простих з c^*. Фактично, коли c->∞ кількість значень, які c^* k + i може набувати в певному діапазоні, зменшується, а, отже, час тестування n зменшується. Для цього методу, слід ділити на всі прості менші ніж c. Спостереження, аналогічні до попереднього, можна застосувати рекурсивно, отримуючи сито Ератосфена. Вдалим способом пришвидшення цих методів (і всіх інших згаданих далі) є попередній обрахунок і зберігання списку всіх простих до певної межі, скажімо всіх простих до 200. (Такий список можна обчислити за допомогою сита Ератосфена). Тоді, перед тестуванням n на простоту з використанням серйозного методу, спочатку перевіряємо чи n не ділиться на якесь просте із цього списку.

Ймовірнісні тести

Найбільш популярними тестами простоти є ймовірнісні тести. Ці тести використовують, крім тестованого числа n, деякі інші числа a , які випадково вибираються з певного набору; звичні рандомізовані тести простоти ніколи не оголошують прості числа складеними, але можливе для складених чисел оголошення їх простими. Імовірність помилки можна зменшити, повторюючи тест з ріними незалежно вибраними a; для двох найчастіше вживаних тестів, для будь-якого складеного n принаймні половина aвизначає складеність n , тому k повторень зменшують імовірність помилки до щонайбільше 2−k. Останню величину можна зробити як завгодно малою, збільшуючи k.

Базова структура рандомізованих тестів простоти є такою:

• Випадково вибрати число a.

• Перевірити певну рівність, що містить a та задане число n. Якщо рівність не виконується, то n є складене число, a називають свідченням складеності, і тест зупиняється.

• Виконувати крок 1, поки не буде досягнуто потрібної певності.

• Після низки повторень, якщо не отримано, що n є складене число, то його можна оголосити імовірнісним простим.

• Найпростішим ймовірнісним тестом простоти є тест простоти Ферма. Це лише евристичний тест; деякі складені числа (числа Кармайкла) будуть оголошені "ймовірнісними простими" незалежно від того, яке свідчення вибране. Проте, він деколи використовується з метою швидкої перевірки числа, наприклад, на фазі утворення ключа криптографічного алгоритму з відкритим ключем RSA.

Тест простоти Міллера-Рабіна та Тест простоти Соловея-Штрассена є вдосконаленими варіантами, які визначають всі складені числа (це означає: для кожного складеного числа n, принаймні 3/4 (Міллер-Рабін) або 1/2 (Соловей-Штрассен) чисел a є свідченнями складеності n). На ці методи часто падає вибір, бо вони набагато швидші, ніж інші загальні тести простоти. Леонард Адлеман та Хуанг запропонували варіант без помилки (але лише з очікуваним поліноміальним часом виконання) тесту простоти на основі еліптичних кривих. На відміну від інших імовірнісних тестів, цей алгоритм дає сертифікат простоти, а тому може бути використаний для доведення простоти числа. Цей алгоритм занадто повільний на практиці.