Развитие управления процессами. Уровни автоматизации

Первый этап. Ручное управление.

Рисунок -

Второй этап. Местное автоматическое регулирование.

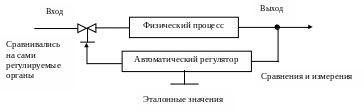
Рисунок -

Третий этап. Централизованное автоматическое регулирование.

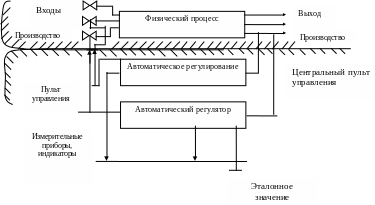
Рисунок -

Недостатки централизованного управления

1. Недостаточная согласованность результатов из-за их зависимости от деятельности операторов.

2. Высокая стоимость регистрации и обработки данных.

3. Невозможность применять оптимальное управление.

4. Большой риск аварий или опасных рабочих режимов

Машинное управление – быстрота вычислений, способность к накоплению данных и принятию решений, выполняют функции:

1. Обработка данных и слежение за ними.

2. Непосредственное и программное управление.

3. Оптимальное управление.

Обработка данных и слежение за ними

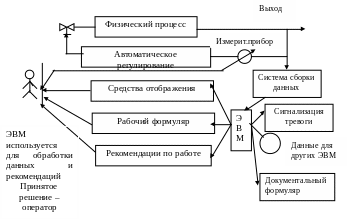
Рисунок -

Автоматический регулятор используют во вспомогательных целях, в главной цепи задействован оператор, использующий ЭВМ.

5.а)Непосредственное управление

Рисунок -

5. б) Программное управление

Рисунок -

6. Оптимальное управление – шаг вперёд по сравнению с 5 уровнем

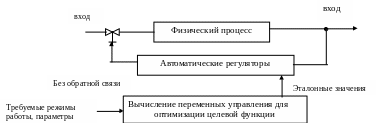
Рисунок -

ЭВМ может выдавать эталонные значения, используя параметры. ЭВМ вычисляет эталонные значения в соответствии с математической моделью, которая обязательна при отсутствии обратной связи. Обратная связь может быть и не быть.

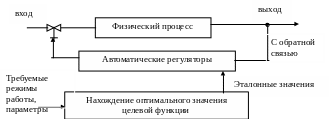
Рисунок -

Наличие модели обязательно. Чаще всего используется комбинация вариантов оптимального управления, когда берётся математическая модель и обратные связи. Можно корректировать модель в процессе управления.

Оптимальный уровень автоматизации

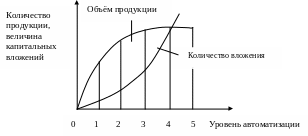
Рисунок -

Кривые, приведены для условий, когда рынок ненасыщенный, продукция реализуется полностью. Кривые могут смещаться от условий.

САР отличаются от САУ тем, что в САУ происходят как формирование, выработка желаемого поведения объекта на основании цели управления в виде управляющих воздействий так и их отработки.

В САР происходит лишь отработка, а само управление воздействия считается заданным.

С точки зрения техники развитие САУ базируется на:

• энергетической революции – создание технической базы, транзист.;

• информационно- компьютерная революция, ПК, управл.ЭВМ;

• информация-замена органов чувств датчиками.

ПЛАНИРОВАНИЕ И ОЦЕНКА РЕЗУЛЬТАТОВ ПРОЦЕССА ПРОЕКТИРОВАНИЯ

Управление процессом проектирования

Задачи теории расписаний и календарного планирования

Предмет теории расписаний. Общие сведения.

Важное практическое значение имеет группа задач, связанных с выполнением комплекса работ (операций, заявок, требований и т.д.) при наличии ограничений на порядок их выполнения, длительность каждой работы, выделяемые ресурсы и т.д.

Существует большая группа задач, которые связаны с выполнением комплекса работ (заявок, расписаний, операций, требований) при наличии ограничений на порядок выполнения работ, на длительность работ, на выделяемые ресурсы и т.д.

Такие задачи возникают при решении вопросов календарного планирования и оперативного управления, как в производстве, так и при обслуживании населения (включая разработку курсовых проектов). Задачи этого типа весьма разнообразны и их исследование производится в рамках различных дисциплин.

1. Теория сетевого планирования.

В теории сетевого планирования – основное внимание уделяется определению порядка выполнения сложных разработок, включающих в себя большое число взаимосвязанных работ, требующих многочисленных исполнителей и в ряде случаев значительных материальных затрат.

2. Теория упорядочения.

В теории упорядочения рассматриваются вопросы для установления порядка выполнения большого комплекса однородных работ с помощью одного или нескольких специализированных устройств, машин, приборов.

3. Теория массового обслуживания.

В теории массового обслуживания^ – разбираются задачи назначения приоритетов в обслуживании поступающих заявок некоторыми устройствами, приборами и т.п.

Однако определённое свойство формальных моделей всех этих видов позволяет объединить их рассмотрение.

Постановки задачи теории расписаний

Целенаправленную деятельность можно рассмотреть как некоторый протекающий во времени процесс, заключающийся в реализации (выполнении) определённой совокупности работ – программы.

При этом выполнение программы стеснено ограничениями, которые можно разбить на 2 вида:

Ограничение а – описывают взаимную зависимость выполнения работ.

Каждой работе P_i  S можно поставить в соответствие некоторое множество предшествующих работ P_i  S, без выполнения которых нельзя начинать выполнение i-той работы P_i, а также ряд работ, не входящих во множество S, но выполнение которых обеспечивает выполнение работы Р_i. К таким работам можно отнести работы, связанные с учётом внешних факторов могут рассматриваться как внешние работы P_i. Например, в строительстве возведение стен P_i можно начинать, когда выполнена разметка, вырыт котлован, сделан фундамент…(П_I - . работа множества S до P_i), а также подвезен кирпич, сделан раствор, произведена доставка рабочих. Эти работы не входят в S.

Для описания некоторых других условий, входящих в а, удобно выполнить дискретизацию времени, то есть разбить его на интервалы и такие интервалы рассматривать как единичные, неделимые. Например, «условный час, день, год». Таким образом все события (начало, окончание работы) привязываются к сети. Ход выполнения работ рассматривается в дискретном времени – единичный интервал времени - t – шаг.

Некоторые работы могут быть выполнены целиком за один шаг, другие – за несколько шагов. В ограничения должно входить условие допустимости или недопустимости прерывания работ.

Пусть – номер рассматриваемого шага ( = 1,2 …) - доля работы P_i, выполняемой на шаге с номером t , которую назовём единичной ( часовой, дневной, годовой …) порцией работы P_i.

S( ) – обозначим перечень работ, выполняемых на шаге ( ).

Пусть работа P_i состоит из m единичных порций y и прерывание этой работы недопустимо.

Условие недопустимости прерывания работы заключается в том, что если эта работа начинается на шаге с номером , то единичные порции должны входить в перечни работ S ( ), S ( +1), …..S ( +m-1).

Ограничение . Они связаны с ограниченным объёмом ресурса, который может быть выделен на выполнение программы S’. Работы на шаге с номером выполняются для этих работ, образующим вектор Q ( ).

Компонентами ресурса Q ( ) могут быть величины: - сырьё, материалы; - оборудование; - рабочая сила; и т.д.

Обозначим через количество ресурса, которое необходимо затратить для выполнения роботы .

Ограничение  имеет вид:

Второе ограничение связано с наличием ресурсов, которые могут быть выделены на выполнение программы. Работа на шаге с номером выполняются ресурсом, который выполнен для всех работ S(t), обозначается он -сырье.

- оборудование

- рабочая сила для данного номера. Количество ресурса, необходимое для выполнения единичной работы y_i(t), обозначается

- сумма для всех работ на каждом шаге по времени ресурса, необходимого для единичных работ y_i(t) не должно превышать суммарного количества ресурсов на данном шаге.

t=1, … m – условие справедливо.

Единичная порция работ y_i(t) либо выполняются полностью, либо не начинается. Считается, что объём работы не зависит от количества выделенных ресурсов.

Более общая задача может быть поставлена, когда учитывается количество выделенного ресурса для решения конкретной задачи.

Суммирование по работам для каждого ,

где - общее число шагов.

Т.о. единичная порция работ либо выполняется полностью, либо не выполняется совсем, если ресурс недостаточен.

Общая и более сложная задача может быть поставлена, когда доля выполненной работы зависит от количества выделенного ресурса.

Задача на составление расписаний сводится к тому, чтобы для каждого шага назвать перечень работ , которые должны выполняться в течение этого шага, а также долю каждой из этих работ с учетом всех ограничений, накладываемых на порядок выполнения работ и на выделяемые ресурсы. В этом случае можно построить график затраты каждого вида ресурса по шагам t выполнения задачи при учёте ограничений на последовательность работ.

Если число работ велико, то число вариантов расписания может быть огромным. Если число работ велико, то количество вариантов начала и окончания промежуточных работ может быть очень большим.

Выбор конкретного варианта связан с понятием директивного срока. Задача автоматизации сводится к рассмотрению возможных вариантов, направленных на снижение директивного срока окончания работ, под которым понимается максимальный по времени путь выполнения работ на общем графе.

Лучшим будет календарный план с минимальным директивным сроком, который можно достичь за счёт перераспределения ресурсов.

Если перечень работ и ресурс на их выполнение заданы, то наилучшим (оптимальным) вариантом будет такой, при котором срок выполнения -min- это директивный срок.

Виды задач на составление расписаний

Задачи на составление расписаний делятся в зависимости от степени жесткости ограничений на очередность выполнения работ.

Первая группа задач. На практике обычно бывает так, что ограничения  на порядок выполнения обычно связывают не все работы, а группы, которые не зависят (или слабо зависят друг от друга – не связаны жесткими ограничениями).

В таких случаях программу работ можно представить в виде некоторого разбиения на ряд самостоятельных подпрограмм R_i, между которыми отсутствуют жесткие ограничения очередности

-программы

-подпрограммы

Внутри каждой подпрограммы порядок выполнения жестко ограничен условиями типа ().

Для решения задач этого типа широко применяются методы: сетевого планирования и управления.

1. На практике обычно последовательно связаны не все работы и можно выделить группы, которые между собой связаны слабо. В этом случае программа S может быть представлена в виде ряда подпрограмм

-групп, которые называются подпрограммами.

Внутри каждой группы порядок следствия работ жёстко связан:

J- параллельно

k- последовательно

Для декомпозиции задач модно использовать деревья “И”. Такие задачи решаются методами сетевого планирования. Графическое представление задач - диаграмма Ганта.

Наимен. работ	Начало	Конец	время	месяц
				дни
1 2 3

Рисунок

Q _cp - количество ресурсов.

Вторая группа задач. Ограничения на очередность слабые. От порядка выполнения работ зависит распределение ресурса по шагам. На переход от одной работы к другой тратится время, необходима переналадка, замена оснастки и оборудования и т.д. Также возникает задача составления наилучшего расписания работ.