Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Орловский филиал РАНХиГС

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика в печать исправленная1.doc

Скачиваний:

Добавлен:

01.04.2025

Размер:

6.51 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Упражнения.

1. Составить уравнение эллипса, если расстояние между фокусами равно 10 (фокусы лежат на оси Ох) и большая ось равна 12.

2. Составить уравнение эллипса, если фокусами служат точки (-2;0) и (2;0), а малая ось равна 8.

3. Составить уравнение эллипса, фокусы которого находятся в точках и , а эксцентриситет .

4. Составить уравнение гиперболы с фокусами на оси Ох, если длина действительной оси равна 12, а расстояние между фокусами равно 20.

5. Составить уравнение гиперболы с фокусами на оси Ох, если длина действительной оси равна 6, а эксцентриситет равен .

6. Составить уравнение гиперболы с фокусами на оси Ох, если длина мнимой оси равна 8, а эксцентриситет равен .

7. Составить уравнение параболы с вершиной в начале координат, ее директрисой служит прямая .

8. Составить уравнение параболы с вершиной в начале координат, симметрично относительно оси Ох и проходящей через точку (5;-3).

9. Составить уравнение параболы с вершиной в начале координат, если ее фокус находится в точке F(5;0).

Индивидуальные задания.

Для данной линии второго порядка найти:

1) полуоси; 2) координаты фокусов; 3) координаты вершин; 4) эксцентриситет; 5) уравнения асимптот (в случае гиперболы). Построить данную линию.

1. ; 2. ; 3. ; 4. ; 5. ; 6. ; 7. ; 8. ; 9. ; 10. ; 11. ; 12. ; 13. ; 14. ; 15. ; 16. ; 17. ; 18. ; 19. ; 20. ;

21. .

Практическая работа № 12. Вычисление производных.

Цель: отработать навыки дифференцирование элементарных и сложных функций.

Методические указания.

Определение. Пусть задана функция , и пусть - некоторая точка интервала . Предел называется производной функции в точке и обозначается . То есть .

Функция, имеющая производную в некоторой точке, называется дифференцируемой в этой точке.

Правило нахождения производной функции в точке по определению:

1. найти разность ;

2. найти отношение ;

3. найти предел этого отношения при .

Пример 1. Найти производную функции .

Решение:

Находим разность .
Находим отношение .
Вычисляем предел .

Таким образом, .

Основные правила дифференцирования.

1. . 2.

3. . 4. .

Производная сложная функции.

или .

Формулы дифференцирования.

При условии	При условии


, n – любое действительное число	, n – любое действительное число









\|u\|<1	\|x\|<1
\|u\|<1

Пример 2. Найти производную функции

Решение: применив последовательно правило вычисления производной суммы и формулы вычисления производной степенной функции , имеем Пример 3. Найти производную функции

Используя правило дифференцирования произведения и соответствующие формулы нахождения производных, получим

Пример 4. Найти производную функции .

Решение: используя правило дифференцирования частного и соответствующие формулы нахождения производных, получим

Пример 5. Найти производную функции .

Решение: полагая , получим .

Пример 6. Найти производную функции .

Полагая , получим . Применяя правило вычисления производной сложной функции, имеем

Пример 7. Найти производную функции .

УПРАЖНЕНИЯ.

1. По определению производной, найти производные следующих функций:

а) ; б) .

2. Найти производные функций:

1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ; 8) ; 9) ; 10) ; 11) .

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ.

Найти производные функций при данном значении аргумента:

1) ; 2) ; 3) ; 4) ; 5) ; 6) ;

7) ; 8) ;

9) ; 10) ;

11) ; 12) ;

13) ; 14) ;

15) .

Практическая работа № 13

ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ЕЕ ГРАФИКА (МНОГОЧЛЕН).

Цель: обобщить схему исследования функций, заданных в виде многочленов и построение графиков функций по данным исследованиям.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ.

Общая схема построения графиков функции.

1) Найти область определения функции.

2) Выяснить, не является ли функция чётной, нечётной или периодической.

3) Найти точки пересечения графика с осями координат (если это не вызывает затруднения).

4) Найти интервалы знакопостоянства функции.

5) Асимптоты графика функции.

6)Найти промежутки монотонности функции и её экстремумы.

7) Найти промежутки выпуклости графика функции и точки перегиба.

8) Построить график, используя полученные результаты исследования.

Правила нахождения экстремумов функции y=f(x) с помощью первой производной.

1. Найти производную .

2. Найти критические точки функции y=f(x), т.е. точки в которых обращается в нуль или терпит разрыв.

3. Исследовать знак производной в промежутках, на которые найденные критические точки делят область определения функции f(x). При этом критическая точка есть минимума, если она отделяет промежуток, в котором , от промежутка, в котором , и точка максимума – в противном случае. Если же в соседних промежутках, раздельной критической точкой , знак производной не меняется, то в точке функция экстремума не имеет.

4. Вычислить значения функции в точках экстремума.

Определение: Прямая y=kx+b называется асимптотой графика функции f(x) при если , где , .

Аналогично определяется и находится асимптота графика функции f(x) при .

Определение: Прямая х=а называется вертикальной асимптотой графика функции , если или .

Пример. Исследовать функцию и построить ее график.

Решение:

1. Функция определена на всей числовой прямой, т.е. D(y)=R.

2. Данная функция, не является ни чётной, ни нечётной: кроме того, она не является периодической.

3. Найдём точку пересечения графика с осью Оу: полагая х=0, получим у=-3. Точки пересечения графика с осью Ох в данном случае найти затруднительно.

4. Очевидно, что график функции не имеет асимптот.

5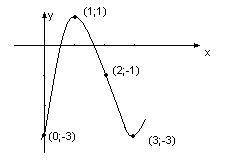 . Найдем производную: Далее имеем, или . Отсюда, х=1 и х=3. Точки х=1 и х=3 делят область определения функции на три промежутка: -∞<x<1, 1<x<3 и 3<x<+∞. В промежутках -∞<x<1, и 3<x<+∞ y>0, т.е. функция возрастает, а в промежутке 1<x<3 , т.е. функция убывает. При переходе через точку х=1 производная меняет знак с плюса на минус, Рис. 1

а при переходе через точку х=3 - с минуса на плюс. Значит, , .

6. Найдём вторую производную: ; 6х-12=0, х=2. Точка х=2 делит область определения функции на два промежутка -∞<x<2 и 2<x<+∞. В первом из них , а во втором , т.е. в промежутке-∞<x<2 кривая выпукла вверх, а в промежутке 2<x<+∞ выпукла вниз. Таким образом, получаем точку перегиба (2;-1);

7. Используя полученные данные, строим искомый график. (рис.1)

УПРАЖНЕНИЯ.

Исследовать данные функции и построить их графики:

1) ; 2) ; 3) ; 4) ;

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ.

Исследовать данные функции и построить их графики:

1) ; 2) ; 3) ;

4) ; 5) ; 6) ;

7) ; 8) ;

9) ; 10) .

Практическая работа № 14

ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ЕЕ ГРАФИКА (РАЦИОНАЛЬНАЯ ФУНКЦИЯ).

Цель: обобщить схему исследования функций, заданных в виде рациональной дроби и построение графиков функций по данным исследованиям.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ.

Общая схема построения графиков функции.

1) Найти область определения функции.

2) Выяснить, не является ли функция чётной, нечётной или периодической.

3) Найти точки пересечения графика с осями координат (если это не вызывает затруднения).

4) Найти интервалы знакопостоянства функции.

5) Асимптоты графика функции.

6)Найти промежутки монотонности функции и её экстремумы.

7) Найти промежутки выпуклости графика функции и точки перегиба.

8) Построить график, используя полученные результаты исследования.

Правила нахождения экстремумов функции y=f(x) с помощью первой производной.

1. Найти производную .

2. Найти критические точки функции y=f(x), т.е. точки в которых обращается в нуль или терпит разрыв.

4. Вычислить значения функции в точках экстремума.

Определение: Прямая y=kx+b называется асимптотой графика функции f(x) при если , где , .

Аналогично определяется и находится асимптота графика функции f(x) при .

Определение: Прямая х=а называется вертикальной асимптотой графика функции , если или .

Пример. Исследовать функцию и построить ее график.

1.Находим область определение функции D(y)= .

2. Данная функция не является нечётной, ни нечётной, ни периодической.

3. При х=0 получим у=0, т.е. график проходит через начало координатой.

4. Так как , то прямая х=3 служит вертикальной асимптотой графика.

Далее находим:

Следовательно, прямая у=х+3 является наклонной асимптотой графика.

5. Находим:

Производная обращайся в нуль в точках х=0 и х=6 и терпит разрыв при х=3. Этими точками числовая прямая делится на четыре промежутка: -∞<x<0, 0<x<3, 3<x<6 и 6<x<+∞. Исследуем значок у’ в каждом из них; очевидно, что в промежутках -∞<x<0, 0<x<3, 3<x<6 и 6<x<+∞.

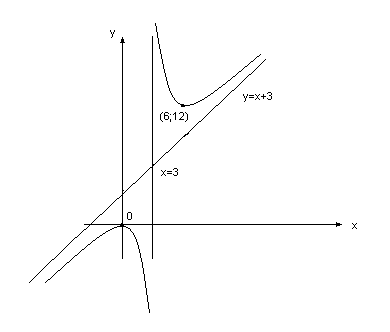И сследуем знак в каждом в каждом из них; очевидно, что y’>0 в промежутках -∞<x<0 и 6<x<+∞ ( в этих промежутках функция убывает). При переходе через точку х=0 производная меняет знак с плюса на минус т.е. эта точка максимума, а при переходе через

х=6 – с минуса на плюс, т.е

Рис. 1

эта точка минимума. Находим: ,

6. Находим

Вторая производная в нуль нигде не обращается и терпит разрыв при х=3. В промежутке -∞<x<3 имеет <0, т.е. в этом промежутке кривая выпукла вверх; в промежутке 3<x<+∞ имеет >0, т.е. в этом промежутке кривая выпукла вниз. Точек перегиба нет.

7. На основании полученных данных строим график функции (рис 1).

УПРАЖНЕНИЯ.

Исследовать данные функции и построить их графики:

1) ; 2) ; 3) .

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ.

Исследовать данные функции и построить их графики:

1) ; 2) ; 3) ; 4) ; 5) ; 6) .

Практическая работа № 15.

ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЕННЫХ ИНТЕГРАОВ.

Цель: отработать основные правила нахождения первообразных функций, освоить основные формулы интегрирования.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ.

Определение: функция F(x) называется первообразной для функции f(x) в промежутке , если в любой точке этого промежутка ее производная равна f(x):

Определение: совокупность первообразных для функции f(x) называется неопределенным интегралом и обозначается символом . Таким образом, .

Здесь f(x)- подынтегральная функция, - подынтегральное выражение, С – произвольная постоянная.

Основные свойства неопределенного интеграла.

Если функция имеет первообразную, то , .
Если - дифференцируемая функция, то , .
Если функция имеет первообразную, то при верно равенство .
Если функция и имеют первообразные, то .

Таблица неопределенных интегралов.

1. ; 2.

3. ; 4. ;

5. ; 6. ;

7. ; 8. ;

9. ; 10.

11. 12.

13.

Пример 1. Для функции , найти первообразную F(x), график которой проходит через точку (2;2).

Решение: так как при всех верно равенство то - одна из первообразных функции . Следовательно, С – некоторая постоянная. Постоянную С находим из условия F(2)=2, то есть откуда . Значит, .