
- •Математика
- •Практическая работа №1. Построение графиков функций с помощью элементарных преобразований.
- •Методические указания.
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа № 6. Решение логарифмических уравнений и неравенств.
- •Методические указания.
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа № 8. Решение тригонометрических уравнений.
- •Методические указания.
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа № 10. Действия над векторами.
- •Методические указания.
- •Прямоугольная система координат.
- •Правила действий над векторами, заданными своими координатами.
- •Скалярное произведение двух векторов.
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа № 11. Построение линий второго порядка.
- •Методические указания.
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа № 12. Вычисление производных.
- •Методические указания.
- •Найдите для функции f(X) первообразную, график которой проходит через точку м:
- •Найдите интегралы:
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа №19. Вычисление объемов и площадей тел вращения.
- •Методические указания.
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа № 20 построение сечений многогранников.
- •Методические указания.
- •Упражнения.
- •Литература.
Индивидуальные задания.
1. Доказать, что
векторы
![]() и
и
![]() взаимно перпендикулярны.
взаимно перпендикулярны.
2. Вычислить длину
вектора
![]() ,
если даны координаты векторов
,
если даны координаты векторов
![]() .
.
3. Вычислить
скалярное произведение
![]() ,
если
,
если
![]() .
.
4. Вычислить длину
вектора
![]() ,
если даны координаты векторов
,
если даны координаты векторов
![]() .
.
5. Вычислить
скалярное произведение
![]() ,
если даны координаты векторов
,
если даны координаты векторов
![]() .
.
6. Найти третью
координату вектора, если даны его
координаты
![]() и длина вектора равна 13.
и длина вектора равна 13.
Практическая работа № 11. Построение линий второго порядка.
Цель: ознакомиться с каноническими видами линий второго порядка, отработать построение линий второго порядка по его каноническому уравнению.
Методические указания.
Эллипсом называется множество точек плоскости, для каждой из которой сумма расстояний до двух данных точек той же плоскости постоянная и больше расстояния между этими точками.
Данные точки называются фокусами эллипса, а расстояние между ними – фокальным расстоянием.
![]() и
и
![]() -
фокусы эллипса,
-
фокусы эллипса,
![]() -
расстояние между фокусами,
-
расстояние между фокусами,
![]() ,
координаты фокусов
,
координаты фокусов
![]() и
и
![]() .
.
Уравнение эллипса,
фокусы которого лежат на оси Ох, имеет
вид
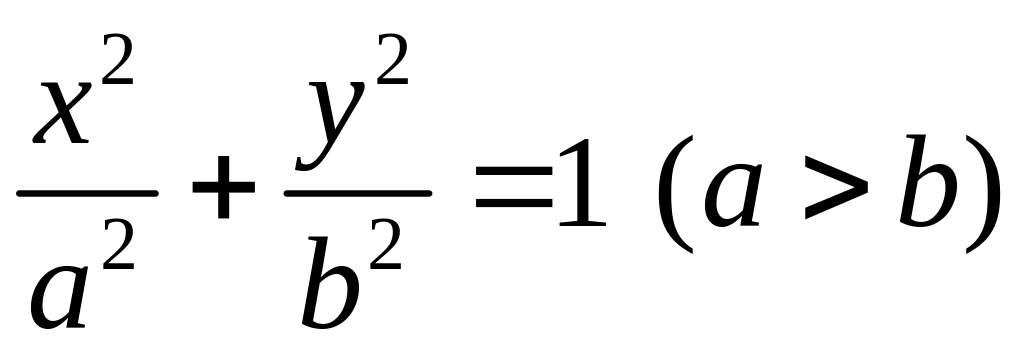 ,
где а – длина большой полуоси, b
– длина малой полуоси (рис. 1).
,
где а – длина большой полуоси, b
– длина малой полуоси (рис. 1).
Зависимость между
параметрами а, b,
c
выражается соотношением
![]() .
.
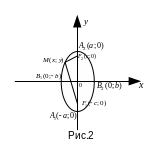
Если фокусы эллипса
лежат на оси Оу, то его уравнение имеет
вид
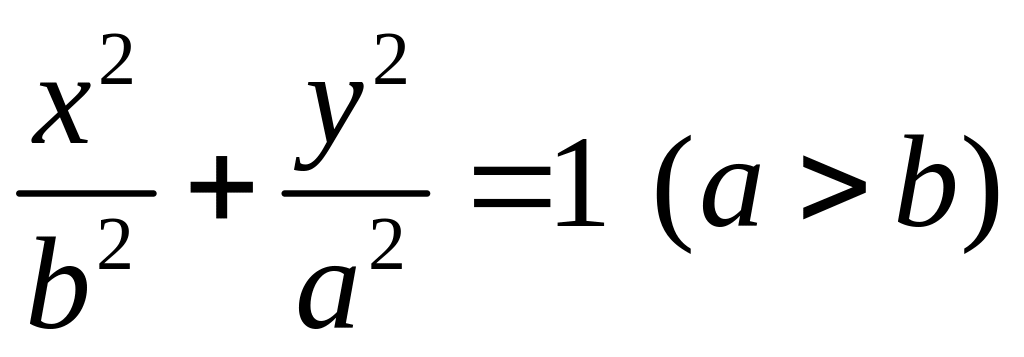 (рис.
2 ).
(рис.
2 ).
Эксцентриситетом
эллипса
называется отношение фокального
расстояния 2с к большой оси 2а:
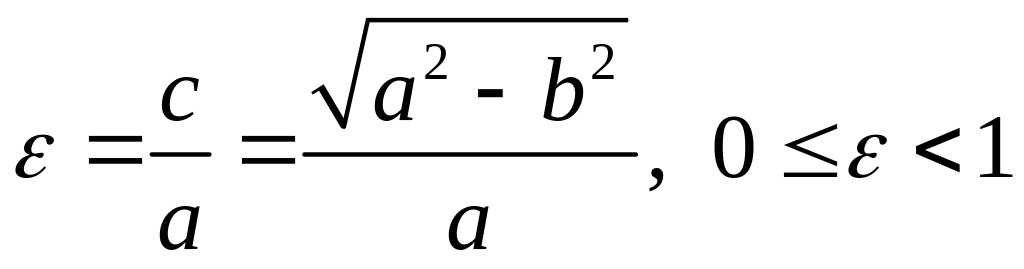 .
.
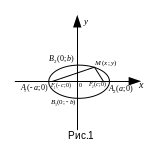
Во всех задачах на эллипс предполагается, что оси симметрии эллипса совпадают с осями координат.
Пример
1. Составить
уравнение эллипса, если его вершины
находятся в точках
![]() и
и
![]() ,
а фокусы – в точках
,
а фокусы – в точках
![]() и
и
![]() .
.
Решение:
из условия следует, что фокусы эллипса
лежат на оси Оу; тогда b=8,
с=6. По формуле
имеем
![]() .
Подставив значения
.
Подставив значения
![]() и
и
![]() в
уравнение
,
получим
в
уравнение
,
получим
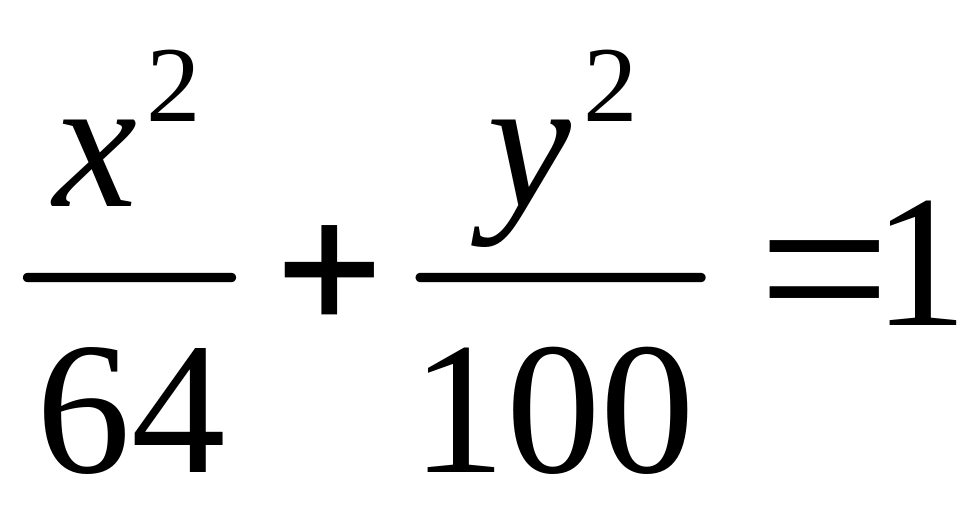 .
.
Пример
2. Составить
уравнение эллипса с фокусами на оси Ох,
если его большая полуось равна 14, а
эксцентриситет
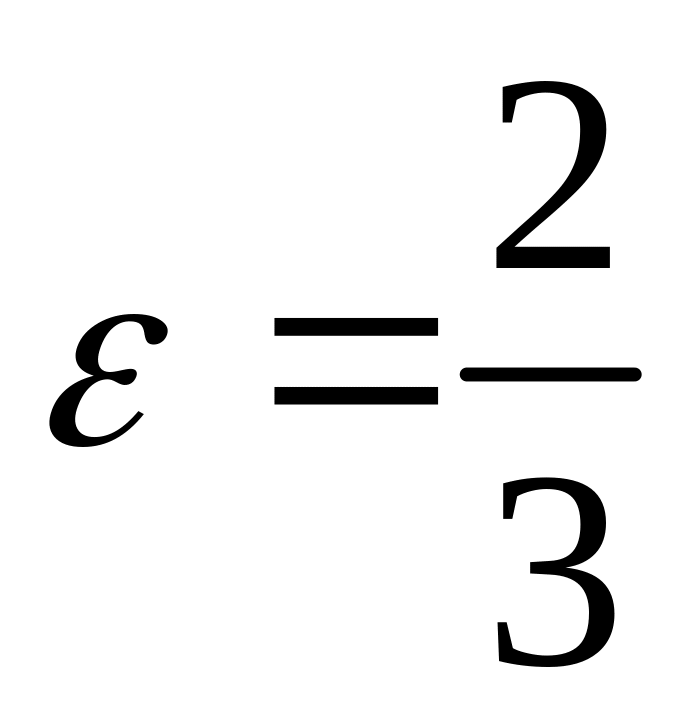 .
.
Решение:
из условия имеем а=7,
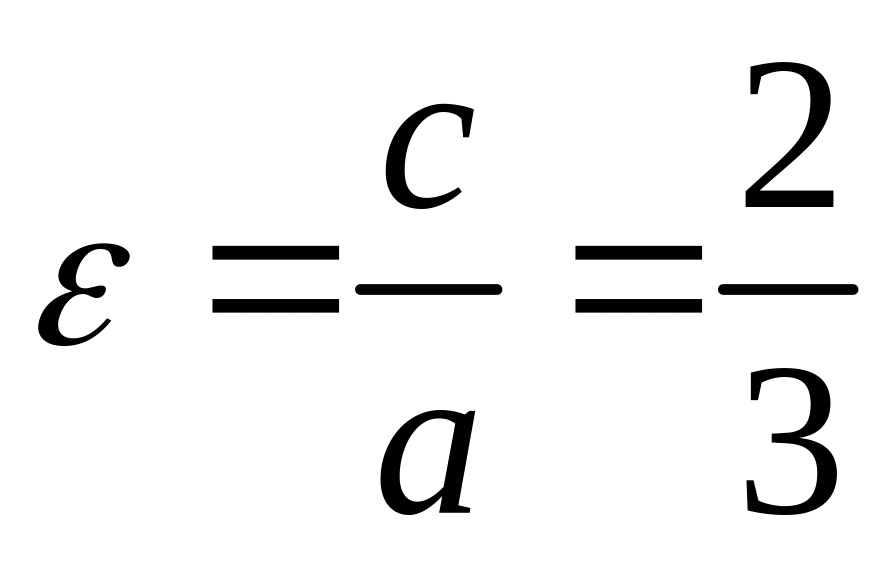 .
Подставив в это соотношение значение
а, получим
.
Подставив в это соотношение значение
а, получим
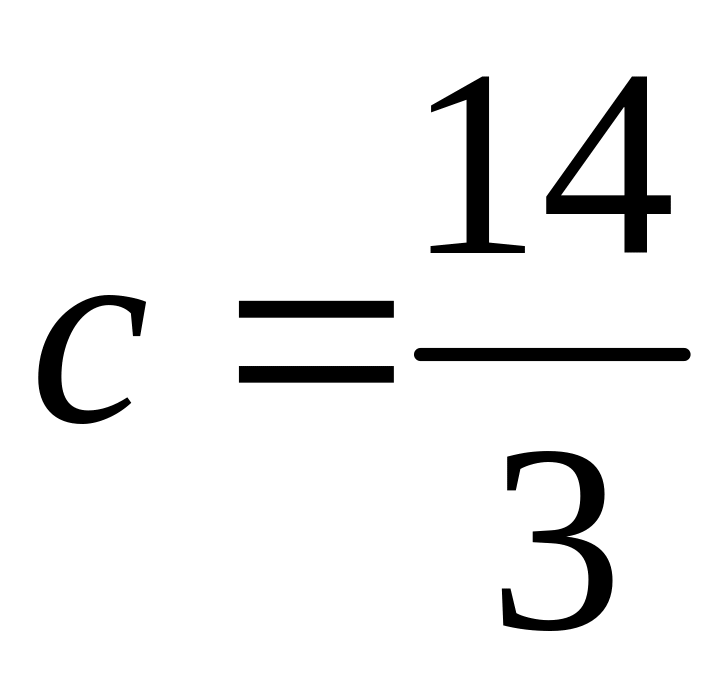 .
.
Далее, находим
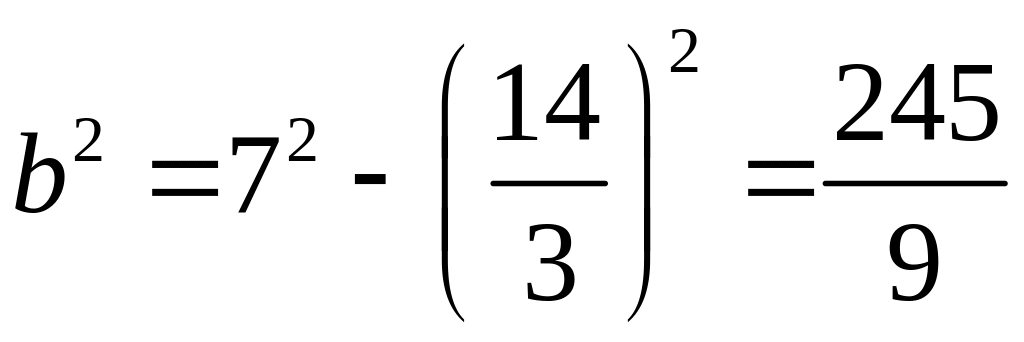 .
Искомое уравнение имеет вид
.
Искомое уравнение имеет вид
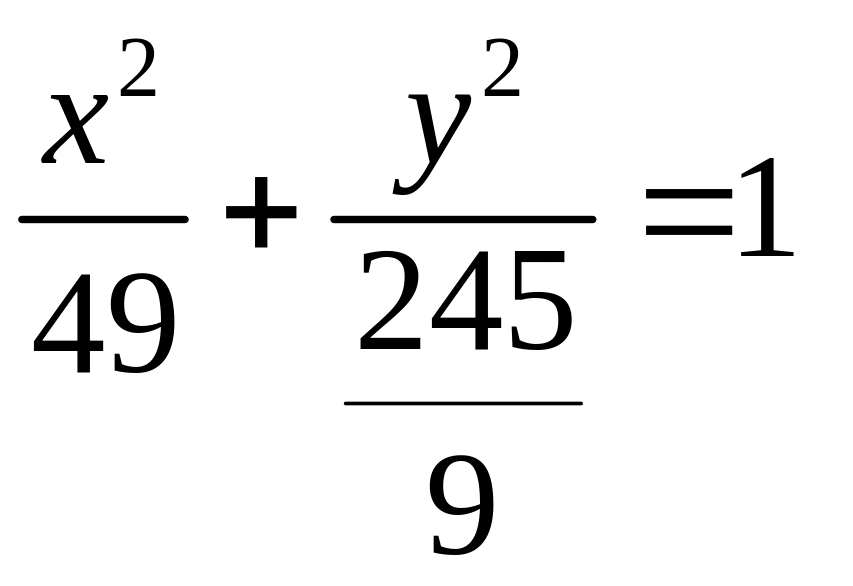 или
или
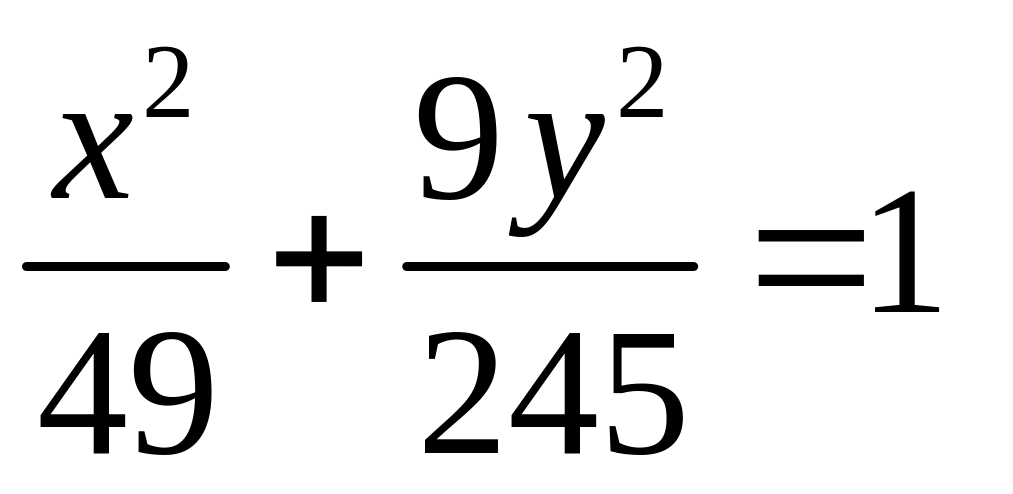 .
.
Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (2а), меньше расстояния между фокусами (2с).
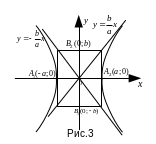
Уравнение гиперболы,
фокусы которой лежат на оси Ох, имеет
вид:
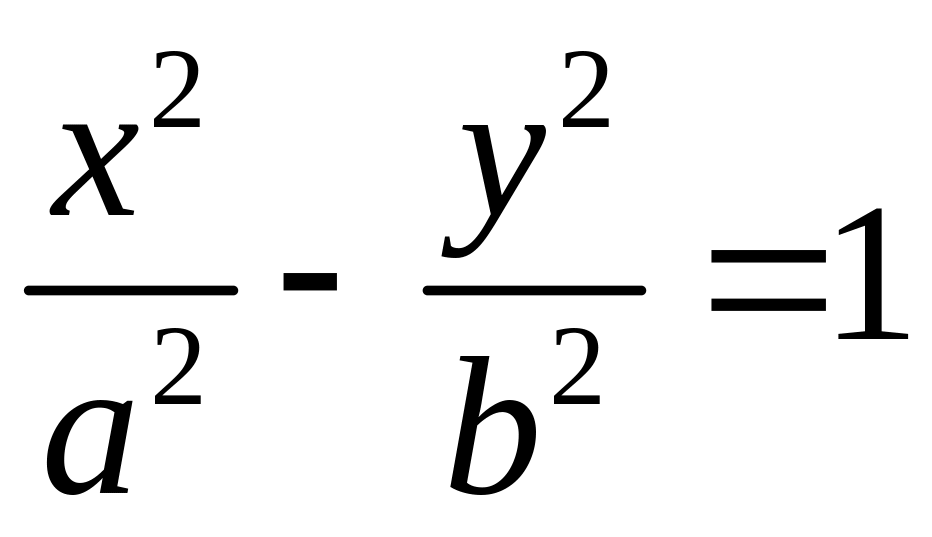 ,
где
,
где
![]() ,
а – длина действительной полуоси, b
- длина мнимой полуоси. (рис.3)
,
а – длина действительной полуоси, b
- длина мнимой полуоси. (рис.3)
Эксцентриситетом
гиперболы
называется отношение фокального
расстояния 2с к большой оси 2а:
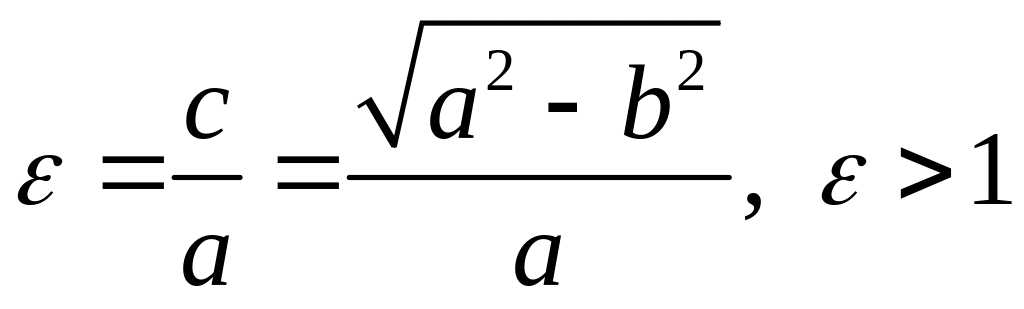 .
.
Гипербола имеет
две асимптоты, уравнения которых
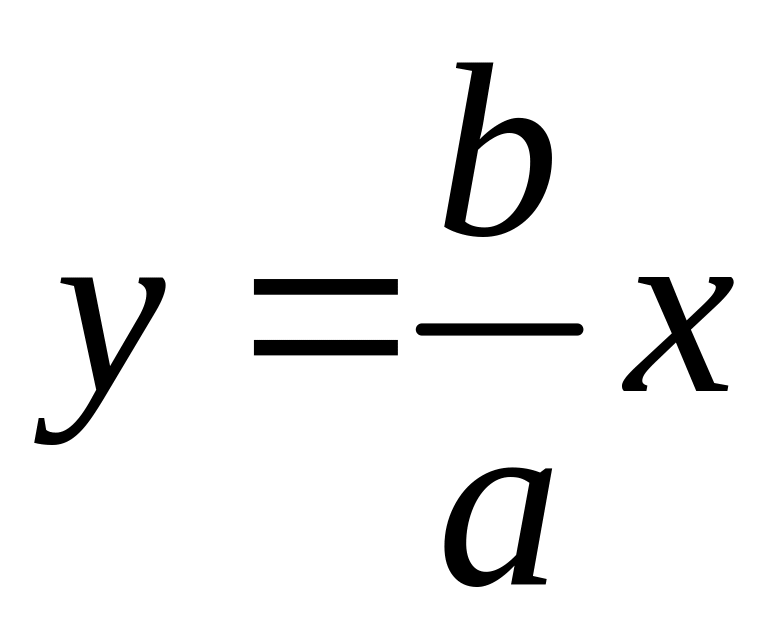 и
и
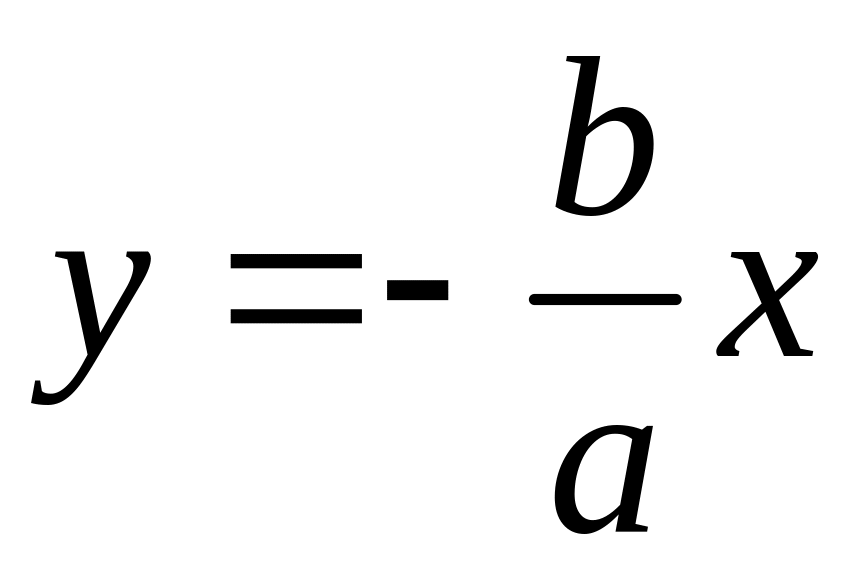 .
.
Если действительная
и мнимая оси гиперболы равны (a=b),
то гипербола называется равносторонней.
Уравнение равносторонней гиперболы
записывается в виде
![]() ,
а уравнения ее асимптот
,
а уравнения ее асимптот
![]() и
и
![]() .
.
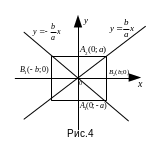
Если фокусы
гиперболы лежат на оси Оу , то ее уравнение
имеет вид:
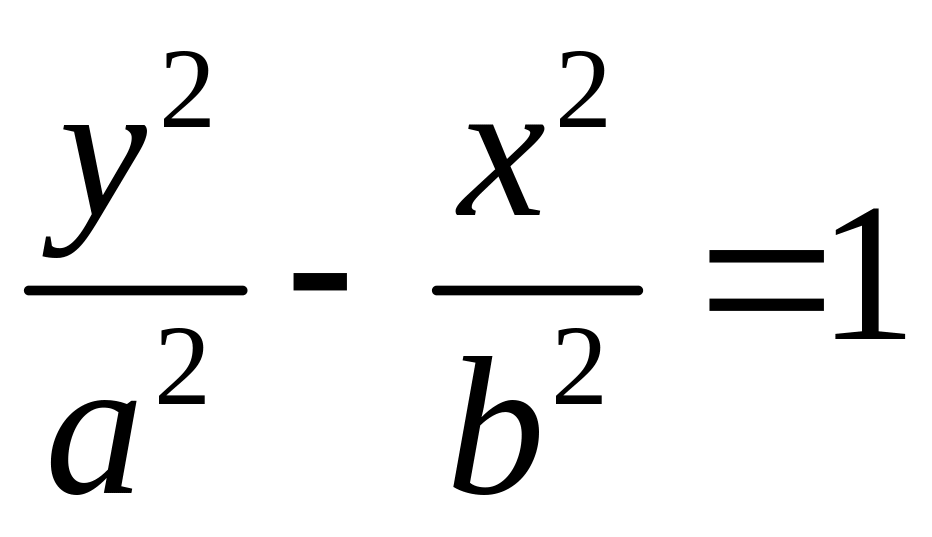 или
или
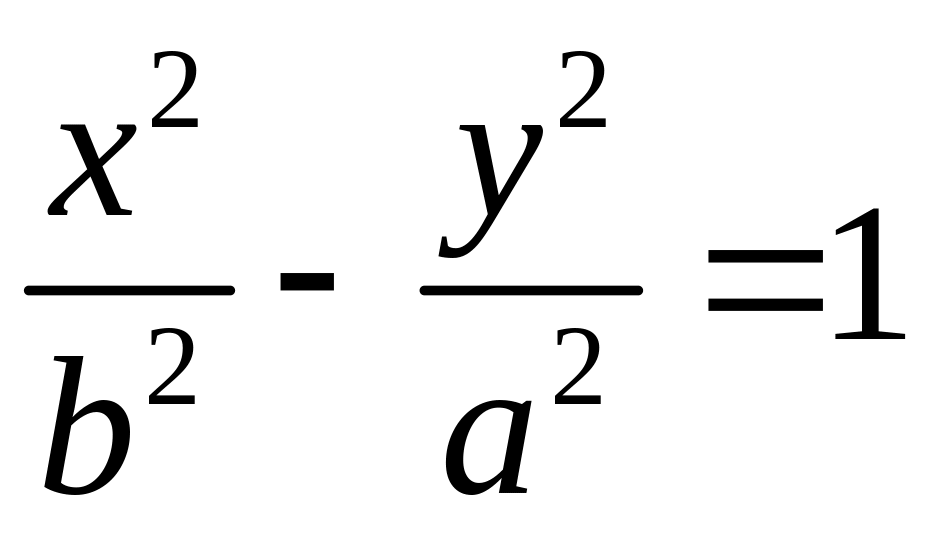 ,
а уравнение асимптот такой гиперболы
,
а уравнение асимптот такой гиперболы
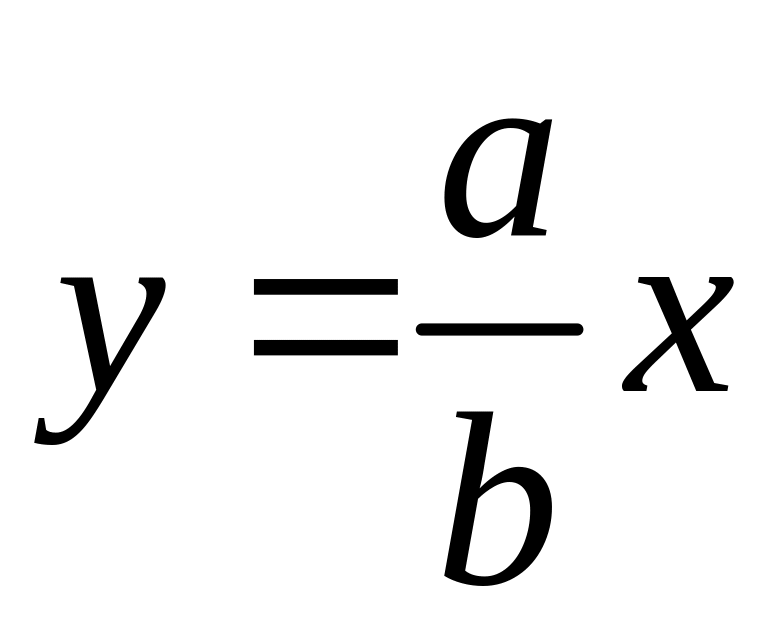 и
и
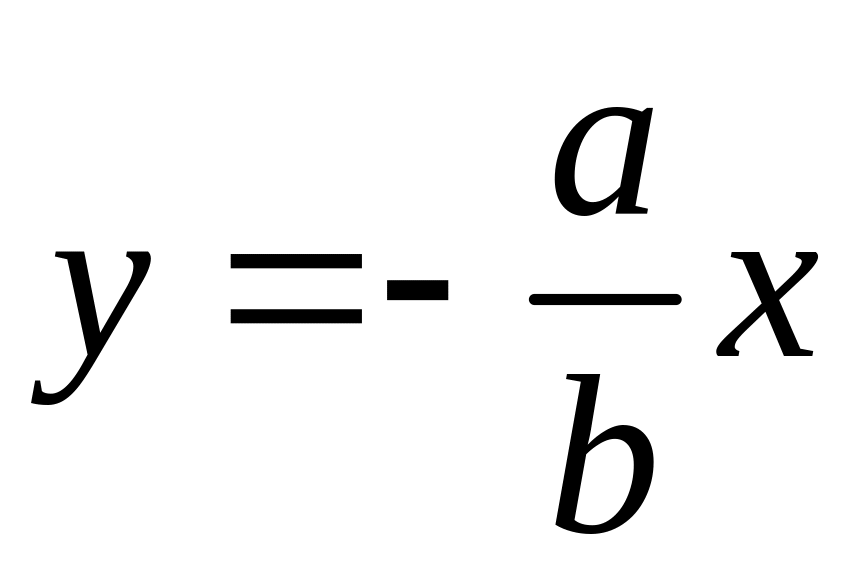 (рис.
4).
(рис.
4).
Пример 3. Составить
уравнение гиперболы, если ее вершины
находятся в точках
![]() и
и
![]() ,
фокусы – в точках
,
фокусы – в точках
![]() и
и
![]() .
.
Решение:
из условия
следует, что а=3 и с=5. по формуле
находим
![]() .
Подставим значения
и
в
уравнение
,
где
,
получим
.
Подставим значения
и
в
уравнение
,
где
,
получим
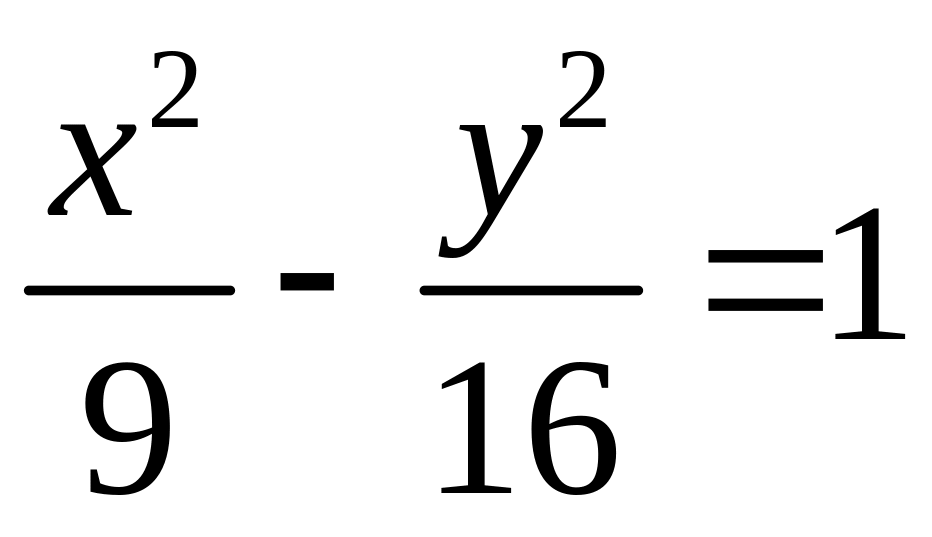 .
.
Пример 4. Найти
вершины, фокусы, эксцентриситет и
асимптоты гиперболы
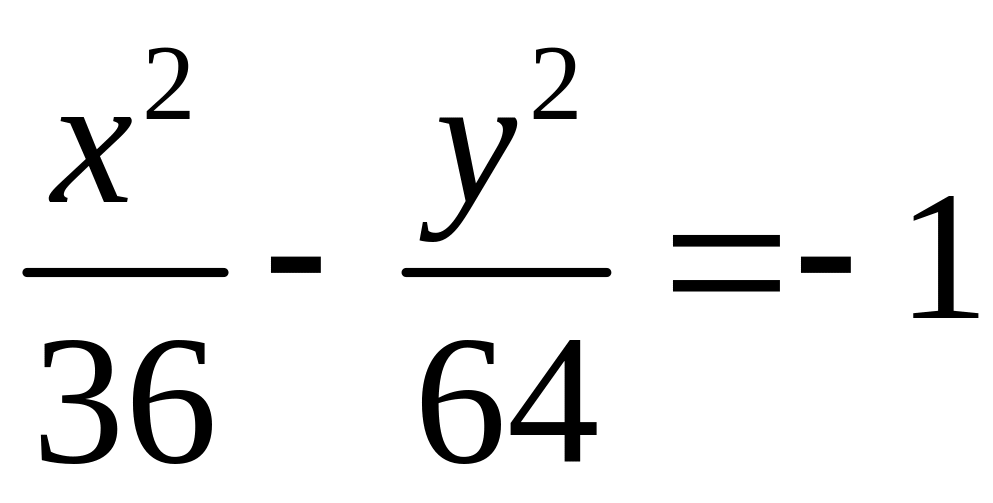 .
.
Решение:
уравнение данной гиперболы имеет вид
,
то есть ее фокусы лежат на оси Оу. Из
условия получим
![]() и
и
![]() .
Вершины гиперболы находятся в точках
.
Вершины гиперболы находятся в точках
![]() и
и
![]() .
По формуле
имеем
.
По формуле
имеем
![]() ,
,
![]() .
Следовательно, фокусами служат точки
.
Следовательно, фокусами служат точки
![]() и
и
![]() .
Эксцентриситет вычислим по формуле
.
Эксцентриситет вычислим по формуле
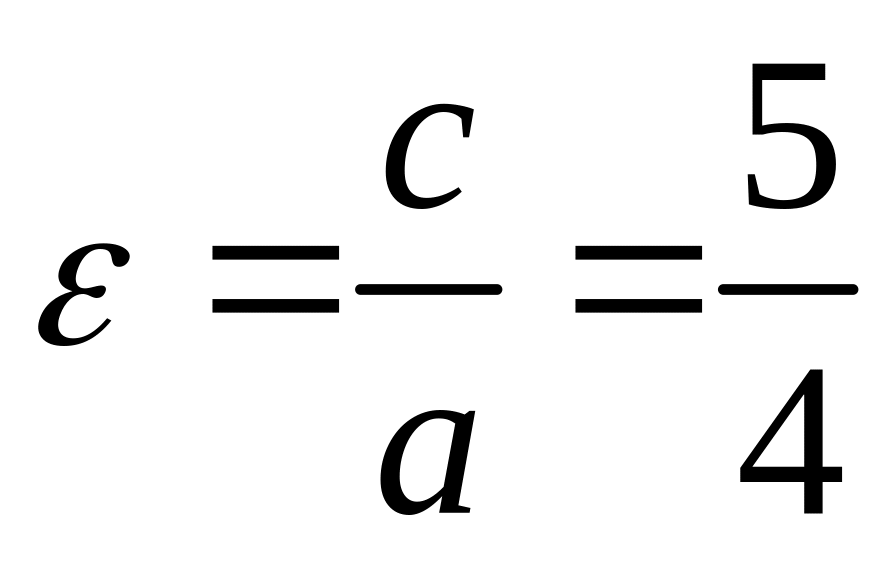 .
Асимптоты гиперболы найдем по формулам
и
,
.
Асимптоты гиперболы найдем по формулам
и
,
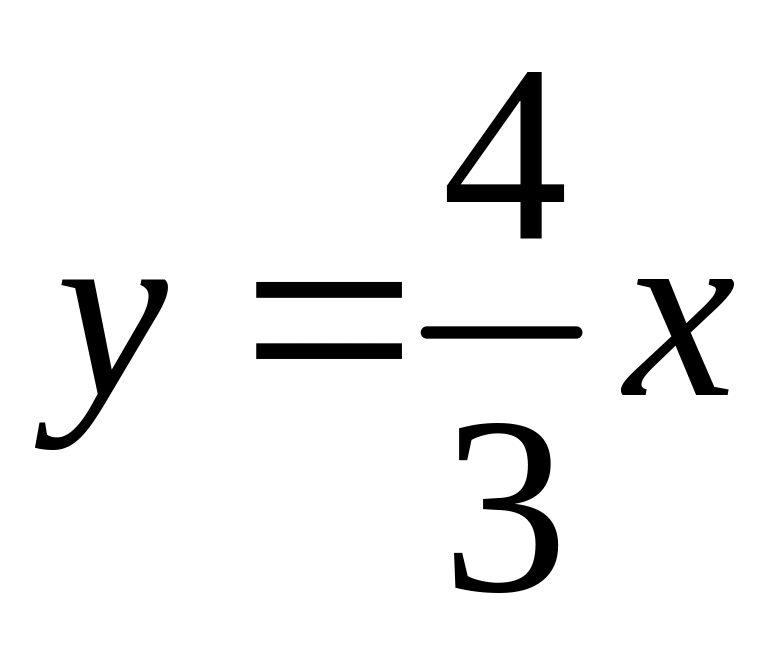 и
и
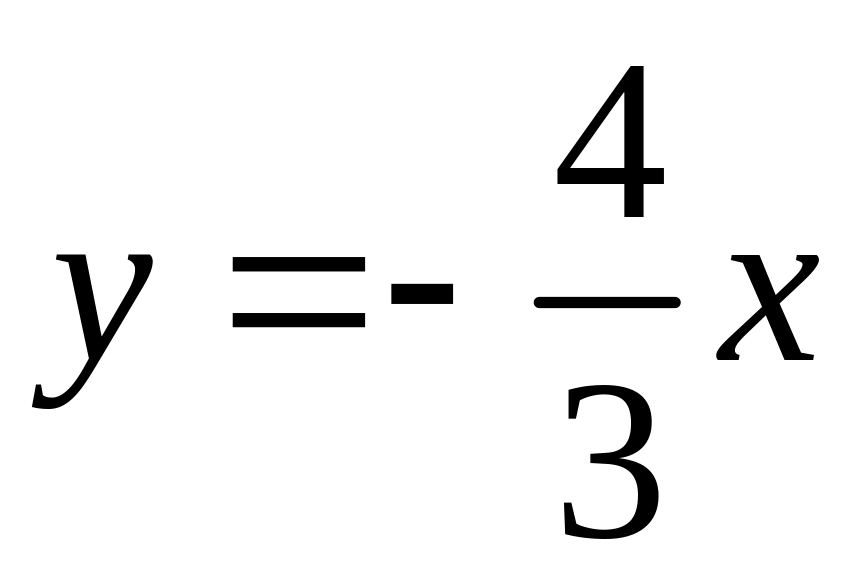 .
.
Параболой называется множество точек плоскости, равноудаленных от данной точки, называемой фокусом, и от данной прямой, называемой директрисой.
Уравнение параболы
с вершиной в начале координат, осью
симметрии которой служит ось Ох и ветви
направлены вправо, имеет вид
![]() ,
где
,
где
![]() (параметры параболы) – расстояние от
фокуса до директрисы (рис.5). Уравнение
ее директрисы
(параметры параболы) – расстояние от
фокуса до директрисы (рис.5). Уравнение
ее директрисы
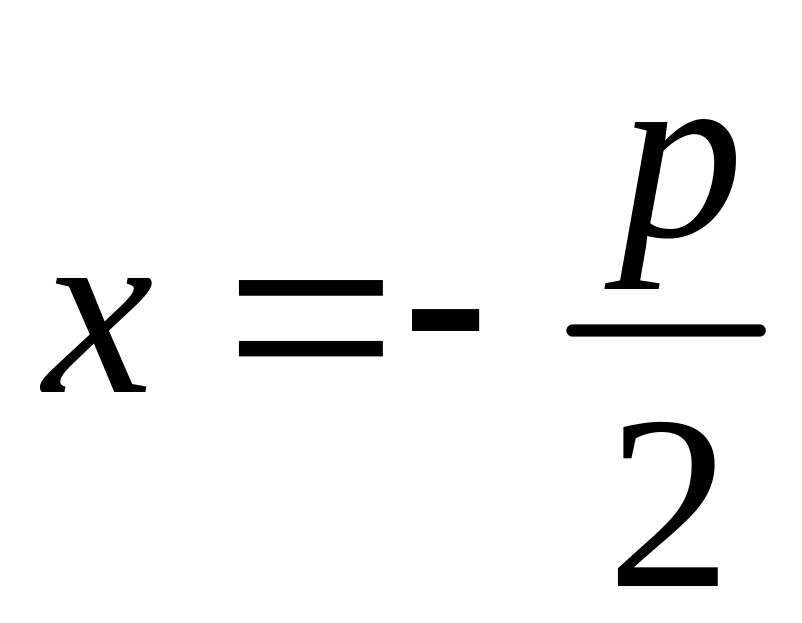 .
.
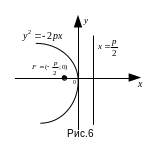
Уравнение параболы
с вершиной в начале координат, осью
симметрии которой служит ось Ох и ветви
направлены влево, имеет вид
![]() ,
(рис.6). Уравнение ее директрисы
,
(рис.6). Уравнение ее директрисы
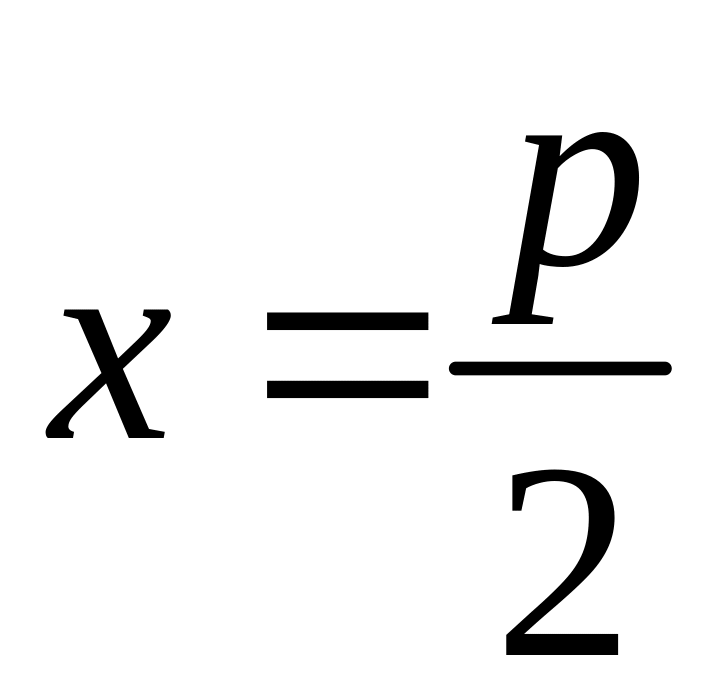 .
.
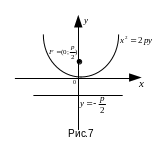
Уравнение параболы
с вершиной в начале координат, осью
симметрии которой служит ось Оу и ветви
направлены вверх, имеет вид
![]() ,
(рис.7). Уравнение ее директрисы
,
(рис.7). Уравнение ее директрисы
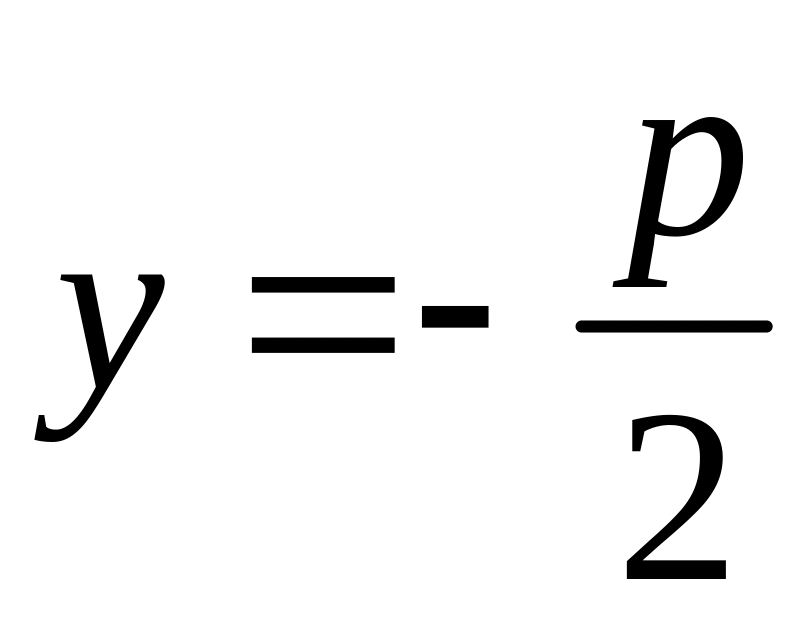 .
.
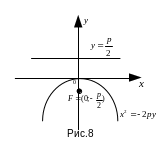
Уравнение параболы
с вершиной в начале координат, осью
симметрии которой служит ось Оу и ветви
направлены вниз, имеет вид
![]() ,
(рис.8). Уравнение ее директрисы
,
(рис.8). Уравнение ее директрисы
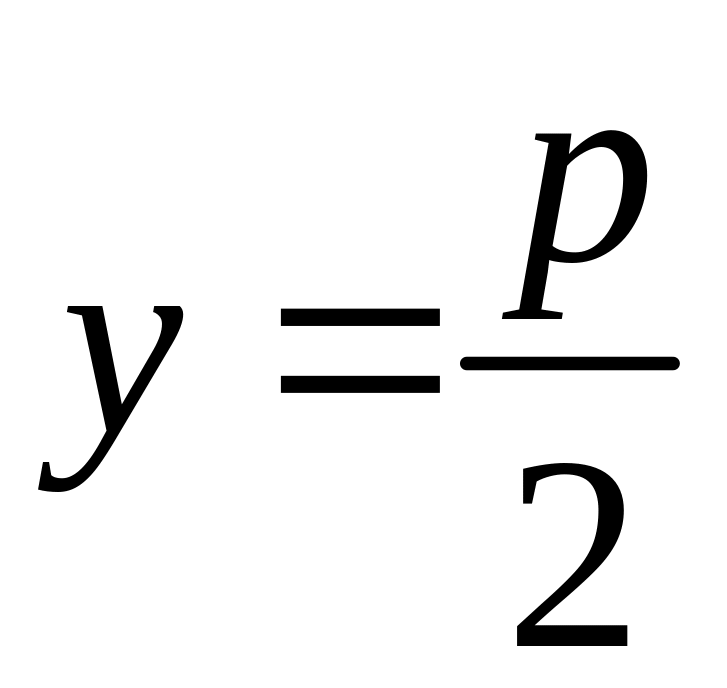 .
.
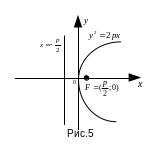
Пример 5. Составить уравнение параболы с вершиной в начале координат, если ее фокус находится в точке F(3;0).
Решение:
фокус параболы лежит на положительной
полуоси Ох, следовательно уравнение
параболы имеет вид
,
так как координаты фокуса
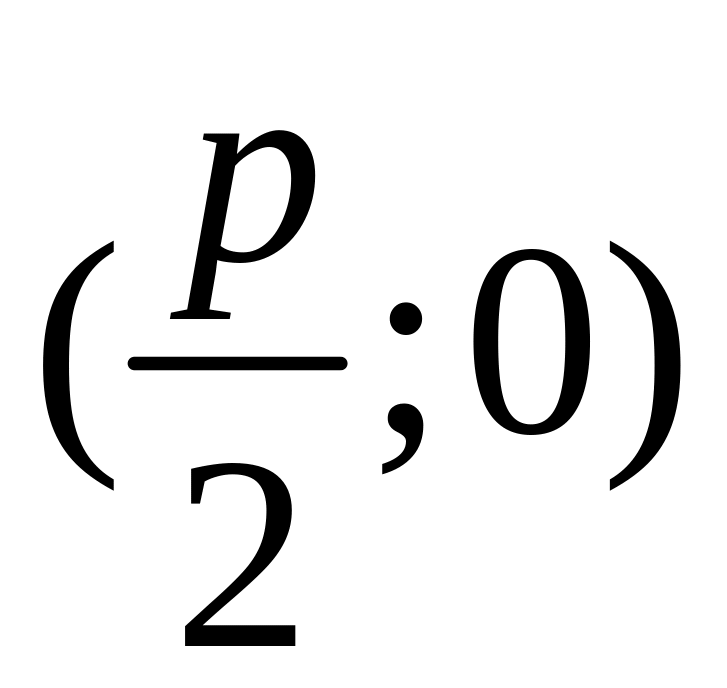 ,
то
,
то
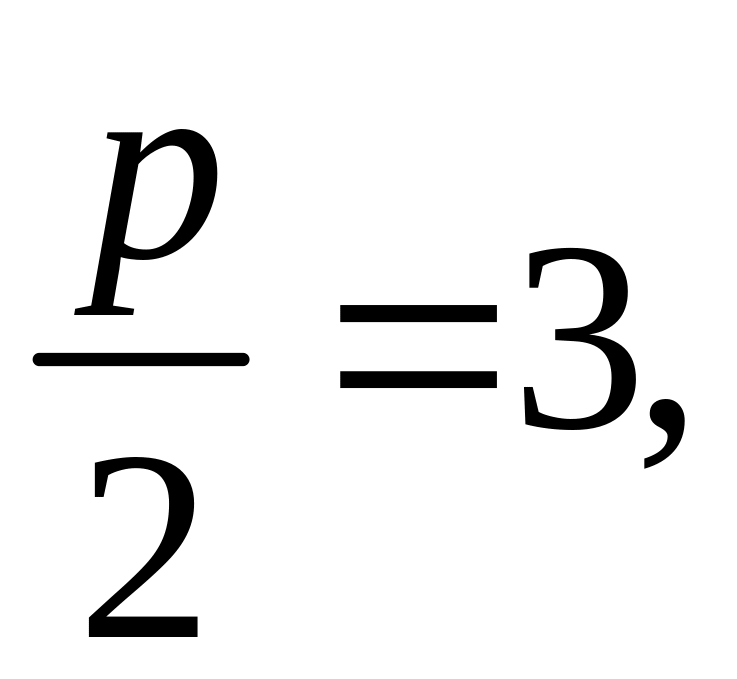 откуда
р=6. Подставим значение р в уравнение
получим
откуда
р=6. Подставим значение р в уравнение
получим
![]() .
.
Пример 6. Составить уравнение параболы с вершиной в начале координат, если ее директрисой служит прямая х=-4.
Решение:
расстояние
директрисы от начала координат равно
![]() ,
следовательно
,
следовательно
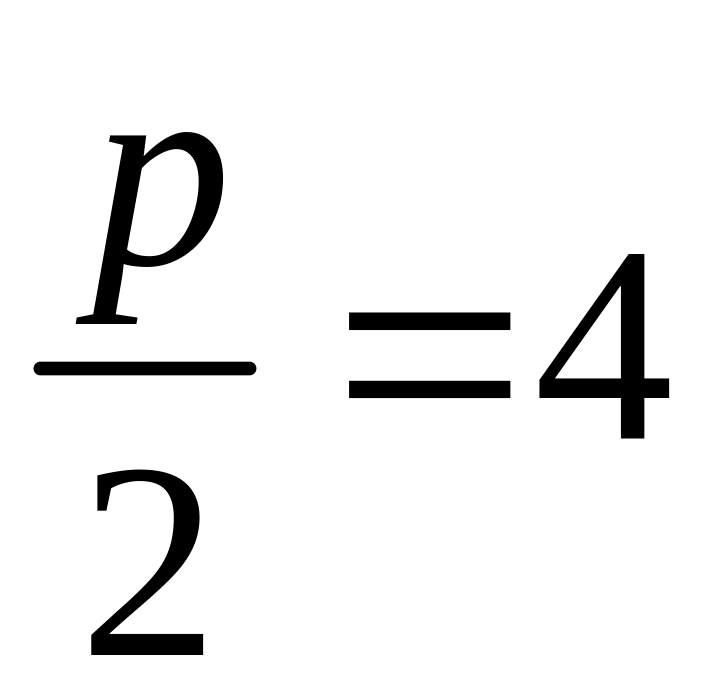 ,
р=8. уравнение этой параболы имеет вид
,
так как абсцисса директрисы отрицательна.
Подставим в уравнение
значение параметра р, получим
,
р=8. уравнение этой параболы имеет вид
,
так как абсцисса директрисы отрицательна.
Подставим в уравнение
значение параметра р, получим
![]() .
.
