Прямоугольная система координат.
Пусть на плоскости
задана пара единичных взаимно
перпендикулярных векторов
и
,
отложенных от некоторого начала- точки
.
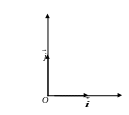
Такую пару
векторов называют прямоугольным базисом
на плоскости. Совокупность начала
и прямоугольного базиса
называют прямоугольной системой
координат на плоскости. Точку
называют началом координат, а векторы
и
-
координатными векторами.
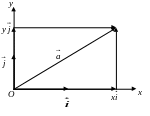
Разложение вектора по координатным осям.
Разложение
вектора
в базисе
имеет вид
;
где - единичный вектор на оси Ох, - единичный вектор на оси Оу.
Числа
и
называются координатами вектора
в базисе
.
Векторы
и
называются
составляющими (или компонентами) вектора
по осям координат. Если начало вектора
находится в точке
,
а конец в точке
,
то разложение вектора
записывается в виде:
.
Правила действий над векторами, заданными своими координатами.
Если в базисе
заданы векторы
и
,
то:
- координаты суммы
двух (или более) векторов равны суммам
соответствующих координат слагаемых,
т.е.
;
- координаты
разности двух векторов равны разностям
соответствующих координат этих векторов,
т.е.
;
- координаты
произведения вектора на число равны
произведениям соответствующих координат
данного вектора на это число, т.е.
;
Пример
1. Найти
координаты вектора
,
если
,
.
Решение:
по формуле
получим
Пример 2. Выразить через единичные векторы и следующие векторы:
1)
;
2)
.
Решение:1)
Здесь
,
.
По формуле
получим
.
2) По формуле
находим
.
Длина вектора
находится по формуле
.
С помощью этой формулы вычисляется
также расстояние между двумя точками
на плоскости.
Пример 3. Найти
длину вектора
,
если
и
.
Решение:
по формуле
находим
Скалярное произведение двух векторов.
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Скалярное
произведение векторов
и
обозначается символов
.
Таким образом,
по определению,
.
Скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого вектора по направлению первого
.
Скалярным квадратом
вектора
называется скалярное произведение
.
Необходимым
и достаточным условием перпендикулярности
двух ненулевых векторов
и
является равенство нулю их скалярного
произведения:
Скалярное
произведение векторов
и
выражается через их координаты по
формуле:
.
Угол между двумя
векторами
и
находится по формуле:
.
Из этой формулы следует, что если векторы
и
перпендикулярны, то
.
Пример 3. Найти
скалярное произведение векторов
и
.
Решение:
по формуле
.
Пример 4. Проверить, перпендикулярны ли векторы:
1)
и
;
2)
и
;
3)
и
.
Решение: по формуле находим:
1)
,
т.е.
;
2)
,
т.е.
;
3
)
,
т.е.
.
Упражнения.
1. Проверьте, перпендикулярны ли векторы:
1)
и
;
2)
и
;
3)
и
.
2. Даны координаты
точек
и
.
Вычислить координаты вектора
.
3. Вычислить длину
вектора
,
если известно разложение векторов
и
по ортам:
.
4. Найти координаты
вектора
,
если даны координаты точек
и
.
5. Вычислить длины
вектора
,
если известно разложение векторов
и
по ортам:
.