Упражнения.

1. Вычислить значения остальных тригонометрических функций угла , если: 1) ; 2) ;

3) ; 4) ;

2. Определить знак выражения: 1) ; 2) ; 3) .

. 3. Упростить выражения:

1) ; 2) ; 3) ; 4) ;

5) .

Индивидуальные задания.

1. Вычислить значения остальных тригонометрических функций угла , если: 1) ; 2) ;

3) ; 4) ;

5) ; 6) ;

7) ; 8) ;

9) ; 10) .

2. Определить знак выражения:

1) ; 2) ; 3) ; 4) ; 5) .

3. Упростить выражения:

1) ; 2) ;

3) ; 4) ; 5) ; 6) ;

7) .

Практическая работа № 8. Решение тригонометрических уравнений.

Цель: отработать методы решения основных видов тригонометрических уравнений.

Методические указания.

Уравнение вида

.

Уравнение вида

,

.

Уравнение вида ,

.

Уравнение вида ,

.

Частные случаи:

, .

, ,

.

Пример 1. Решить уравнение .

Решение: решение данного уравнения можно записать в виде . Так как , то

. Отсюда .

Пример 2. Решить уравнение .

Решение: решение данного уравнения можно записать в виде . Так как , то

. Отсюда .

Пример 3. Решить уравнение .

Решение: это частный случай, и поэтому , .

Пример 4. Решить уравнение (уравнение, сводящееся к квадратному).

Решение: учитывая, что , получим . Сделаем замену , получим квадратное уравнение . Решение данного уравнения , -не удовлетворяет условию . Тогда . Откуда .

Пример 5. Решить уравнение (уравнение однородное относительно ).

Решение: заменим , получим . Разделим обе части уравнения на , получим квадратное уравнение относительно , . Решая последнее уравнение, получим или .

Ответ: , .

УПРАЖНЕНИЯ.

Решить уравнение: 1) ; 2) ; 3) ;

4) ; 5) ; 6) ;

7) ; 8) ; 9) ; 10) .

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ.

1) ; 2) ;

3) ; 4) ;

5) ; 6) ;

7) ; 8) ; 9) ; 10) .

Практическая работа № 9.

ВЫЧИСЛЕНИЕ УГЛОВ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ, ПЛОСКОСТЯМИ.

Цель: отработать основные приемы решения задач на вычисление углов между прямыми, прямой и плоскостью, плоскостями.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ.

Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости α, а точка Н – основание перпендикуляра. Отметим в плоскости α какую–нибудь точку М, отличную от Н, и проведем отрезок АМ. Он называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок НМ – проекция наклонной на плоскость (рис. 1).

Перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости. Длина перпендикуляра, проведенного из точки А к плоскости α, называется расстоянием от точки А до плоскости α.

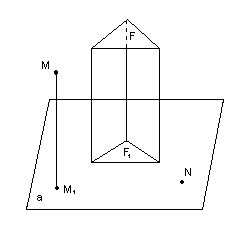Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости. На рисунке 2 точка М₁ – проекция точки М на плоскость α, а N – проекция самой точки N на ту же плоскость, треугольник F₁ – проекция треугольника F на плоскость α.

Углом между прямой и плоскостью,

пересекающей эту прямую и не перпендикулярной Рис. 2

к ней, называется углом между прямой и ее проекцией на плоскость.

Д вугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости. Полуплоскости, образующие двугранный угол, называются его гранями. Прямая а - ребро двугранного угла.

Угол, образованный лучами, проведенными перпендикулярно к ребру, называется линейным углом двугранного угла (рис. 3).

Все линейные углы двугранного угла равны друг другу.

Г радусной мерой двугранного угла называется градусная мера его линейного угла. Если угол - тот из четырех углов, который не превосходит каждого из остальных, то говорят, что угол между пересекающимися плоскостями равен . Очевидно, .

Пример 1. Расстояние от точки М до каждой из вершин правильного треугольника равно 4 см. Найти расстояние от точки М до плоскости АВС, если АВ=6 см. (Рис. 4)

Решение: по условия МА=МВ=МС=4 см. Пусть МО АВС, тогда ОА=ОВ=ОС, как проекции равных наклонных. Рис. 4

Значит, О – центр окружности, описанной около , а ОА – радиус этой окружности. , где АВ= , R=АО поэтому АО= . Из : MO= MO= =2. Ответ: 2 см.

Пример 2. Наклонная АМ, проведенная из точки А к данной плоскости, равна d. Чему равна проекция этой наклонной на плоскость, если угол между прямой АМ и данной плоскость равен 45⁰.

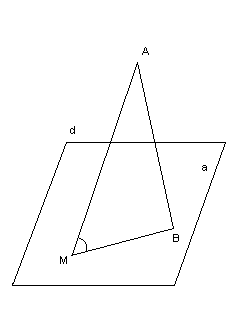Решение: МВ – проекция наклонной АМ на плоскость. - прямоугольный. . Ответ: .

Пример 3. Треугольник АВС – прямоугольный ( ), , АС=а, , . Чему равен угол между плоскостями и .

Решение: 1) , , значит, ; - искомый.

2) из : (катет противолежащий 30⁰).

3) Рассмотрим

. . Ответ: