
- •Математика
- •Практическая работа №1. Построение графиков функций с помощью элементарных преобразований.
- •Методические указания.
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа № 6. Решение логарифмических уравнений и неравенств.
- •Методические указания.
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа № 8. Решение тригонометрических уравнений.
- •Методические указания.
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа № 10. Действия над векторами.
- •Методические указания.
- •Прямоугольная система координат.
- •Правила действий над векторами, заданными своими координатами.
- •Скалярное произведение двух векторов.
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа № 11. Построение линий второго порядка.
- •Методические указания.
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа № 12. Вычисление производных.
- •Методические указания.
- •Найдите для функции f(X) первообразную, график которой проходит через точку м:
- •Найдите интегралы:
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа №19. Вычисление объемов и площадей тел вращения.
- •Методические указания.
- •Упражнения.
- •Индивидуальные задания.
- •Практическая работа № 20 построение сечений многогранников.
- •Методические указания.
- •Упражнения.
- •Литература.
Упражнения.
Вычислить:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() ;
5)
;
5)
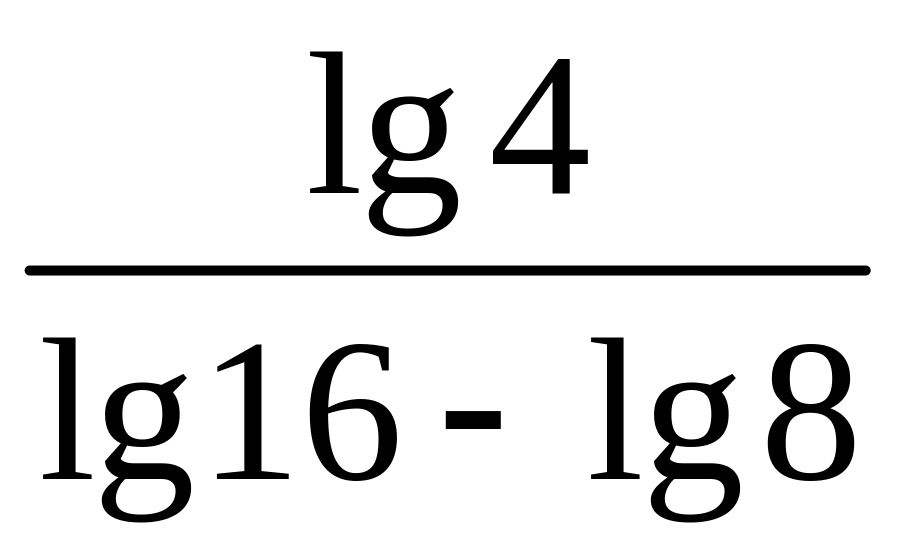 ;
6)
;
6)
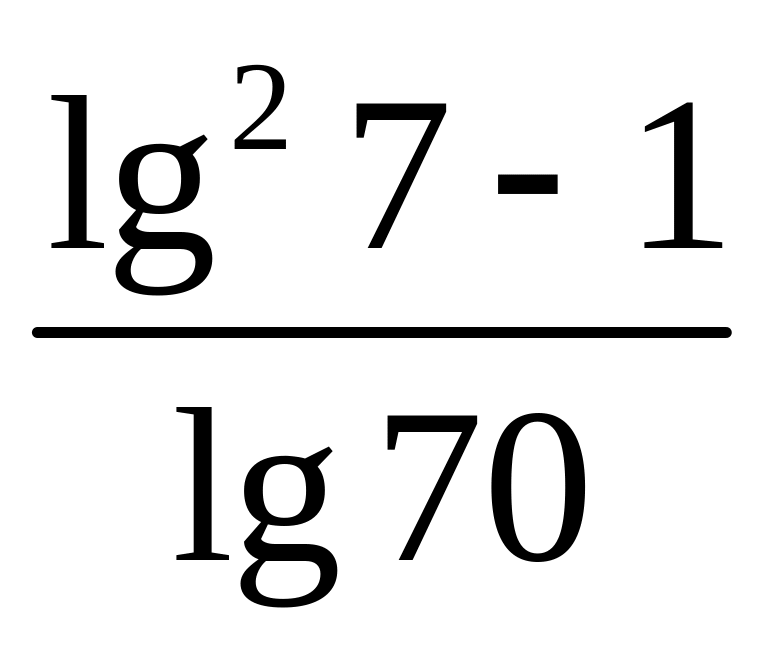 ;
7)
;
7)
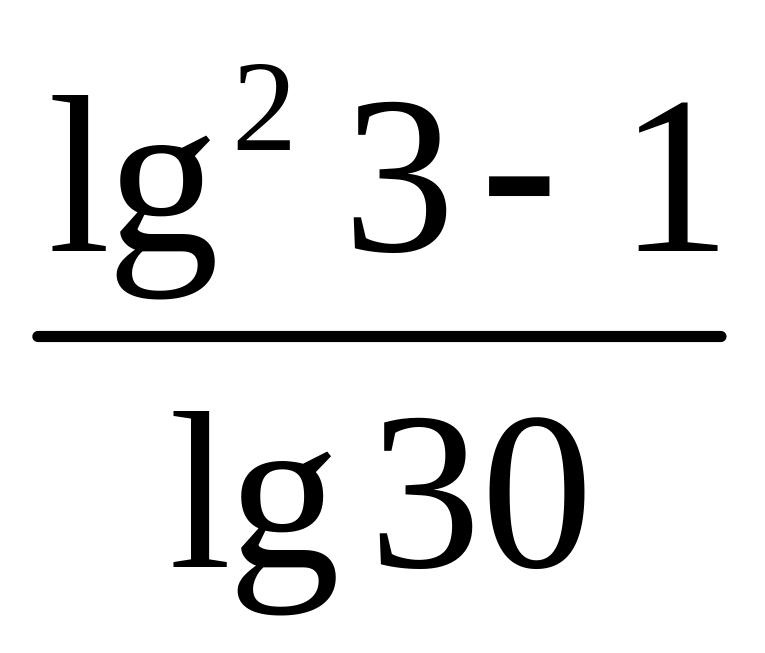 .
.
Прологарифмировать по основанию 10: 1)
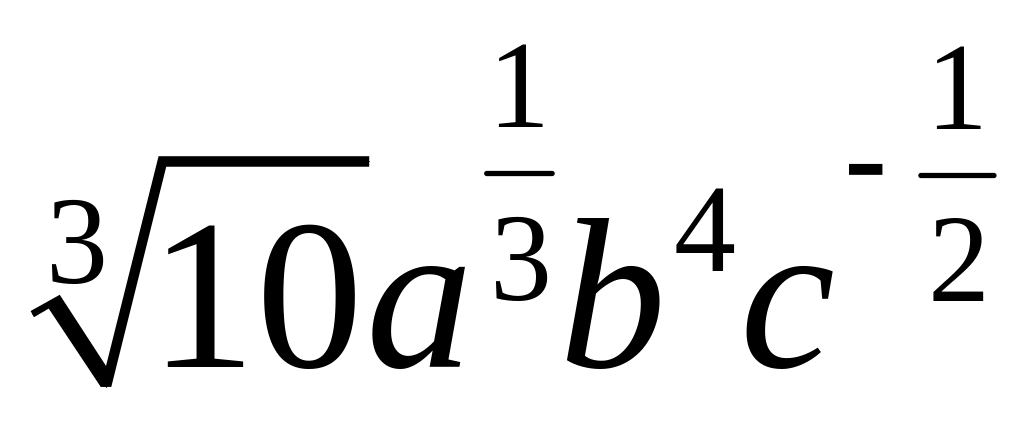 ;
2)
;
2)
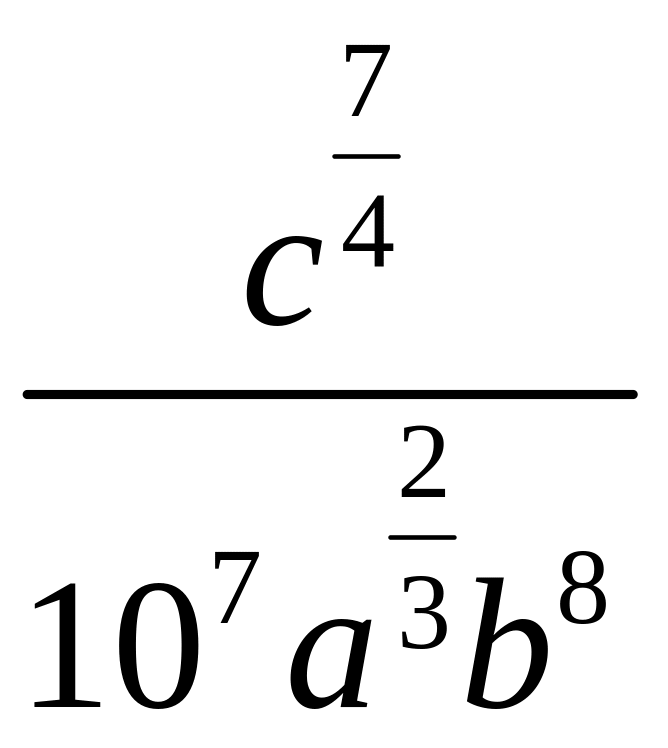 .
.Найти х, если 1)
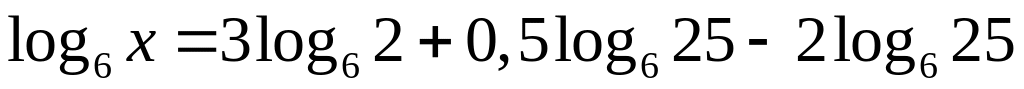 ;
2)
;
2)
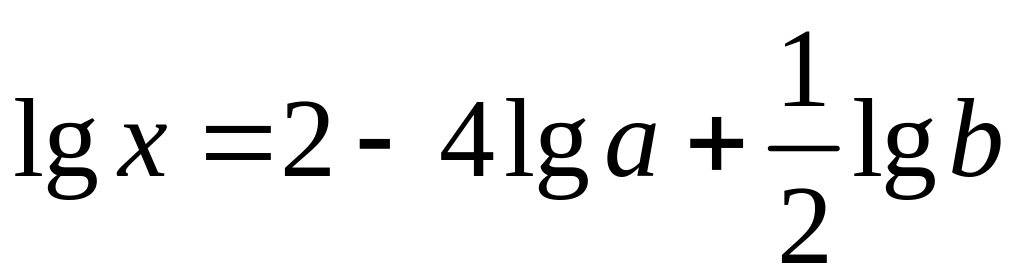 ;
3)
;
3)
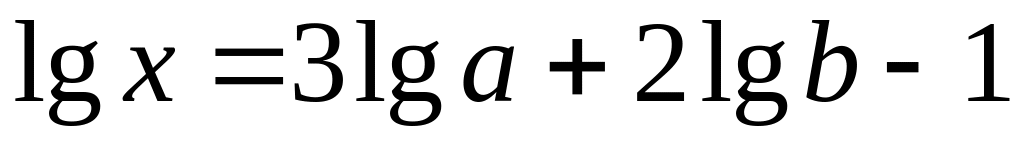 .
.
Индивидуальные задания.
1. Вычислить:
1)
![]() ;
2)
;
2)
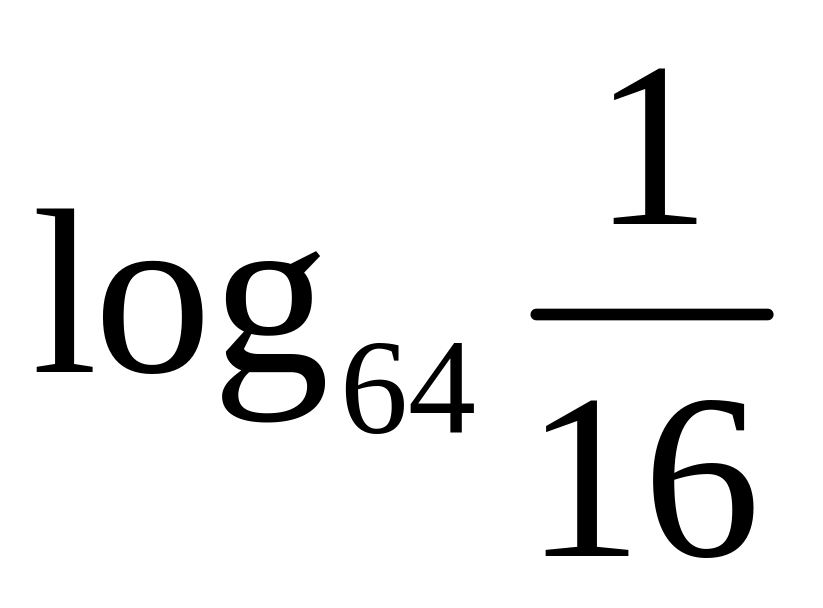 ;
3)
;
3)
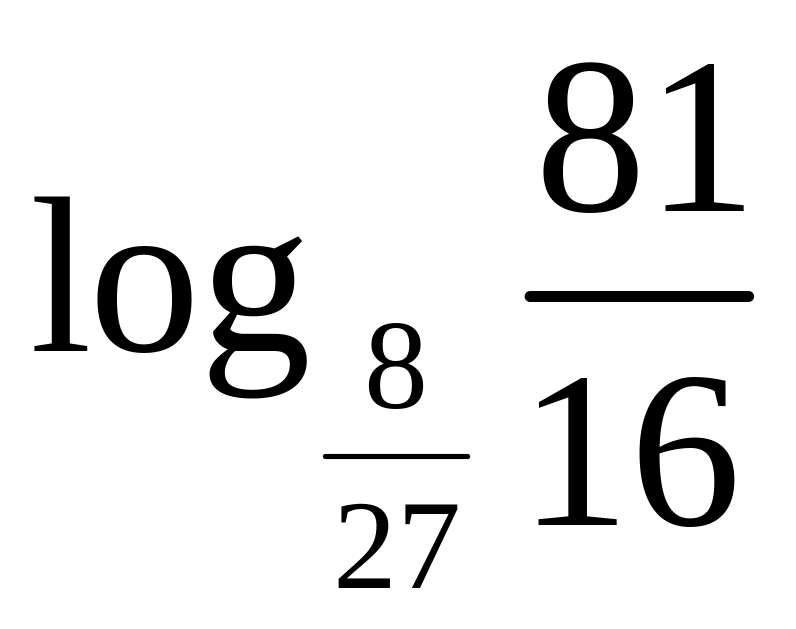 ;
4)
;
4)
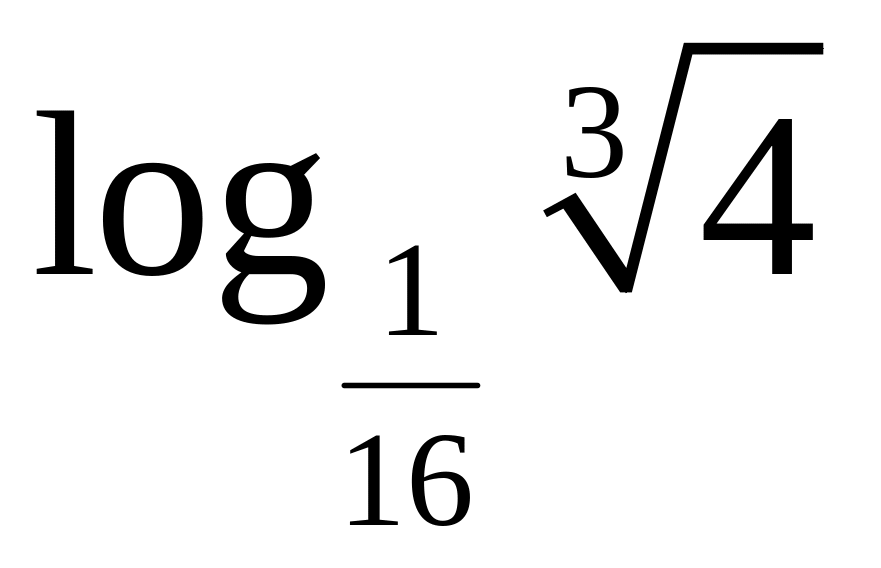 ;
5)
;
5)
![]() ;
;
6)
![]() ;
7)
;
7)
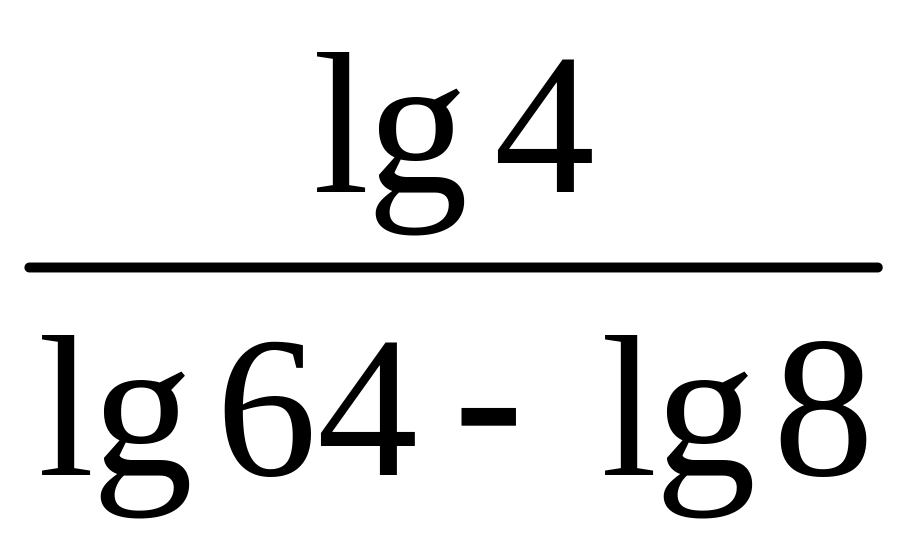 ;
8)
;
8)
![]() ;
9)
;
9)
![]() ;
10)
;
10)
![]() .
.
2. Прологарифмировать:
а) по основанию
10: 1)
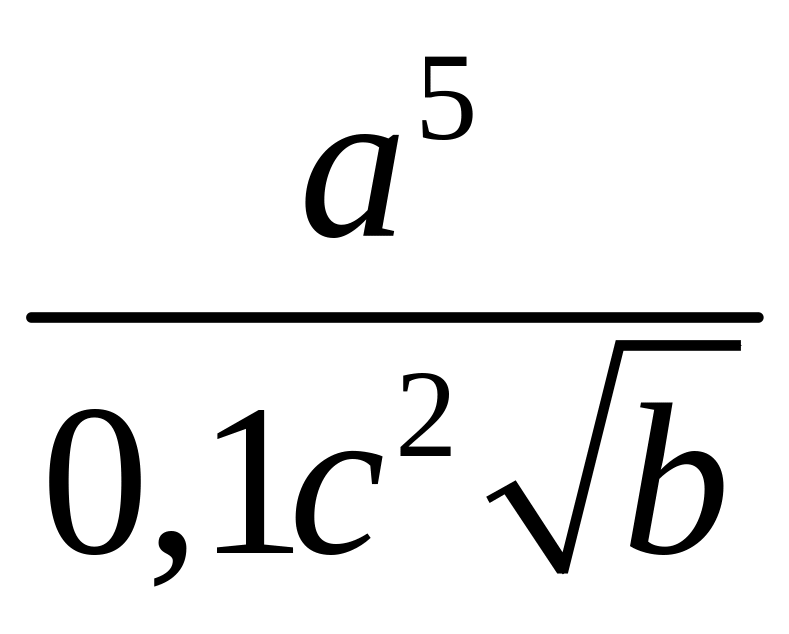 ;
2)
;
2)
![]() ;
3)
;
3)
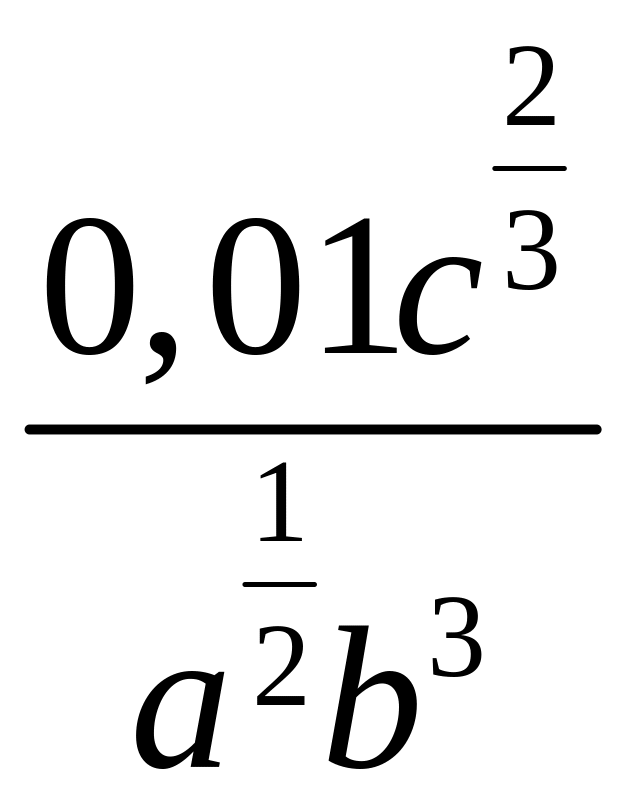 ;
4)
;
4)
![]() ;
5)
;
5)
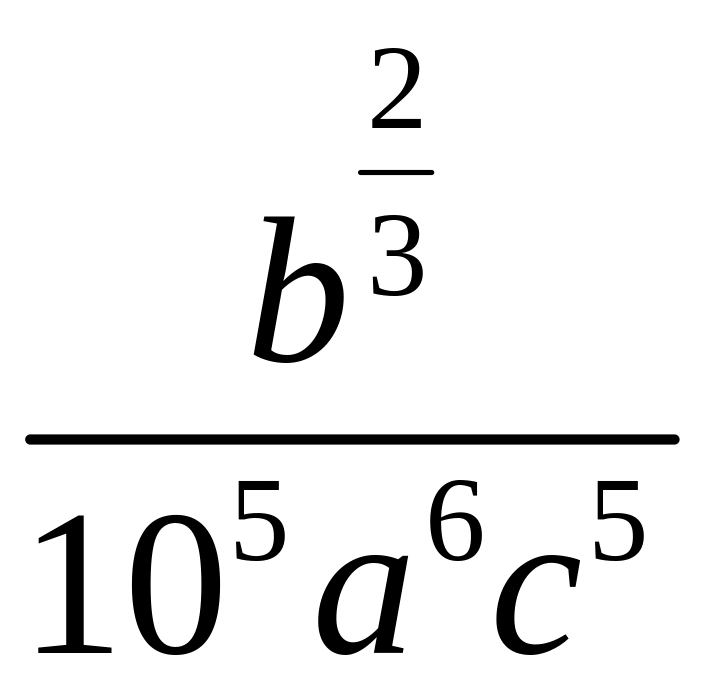 ;
;
б) по основанию
3: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
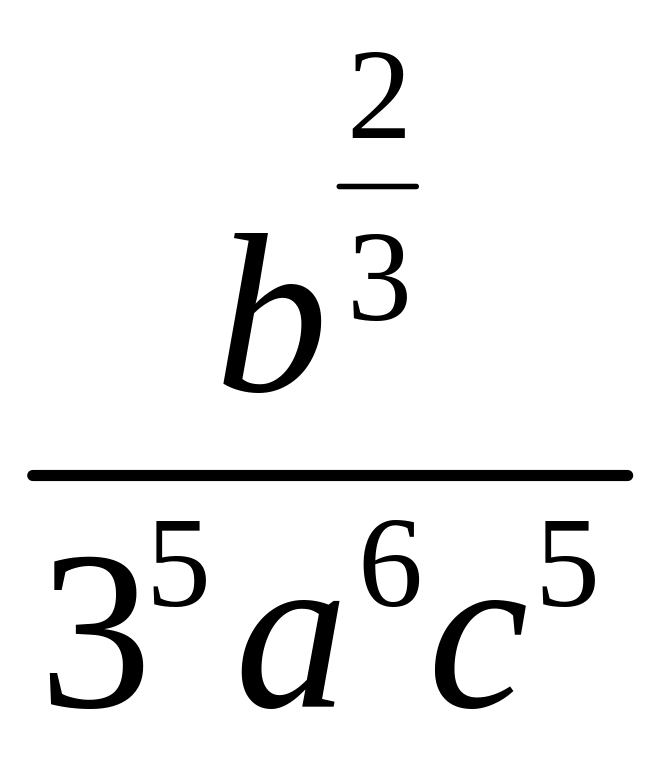 .
.
Найти х, если 1)
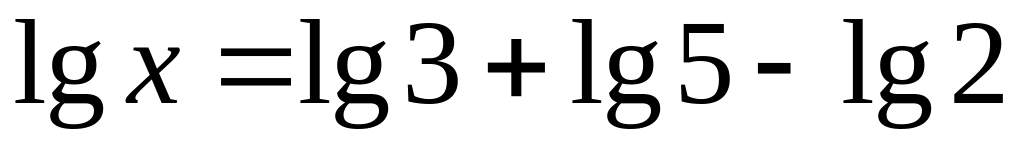 ;
2)
;
2)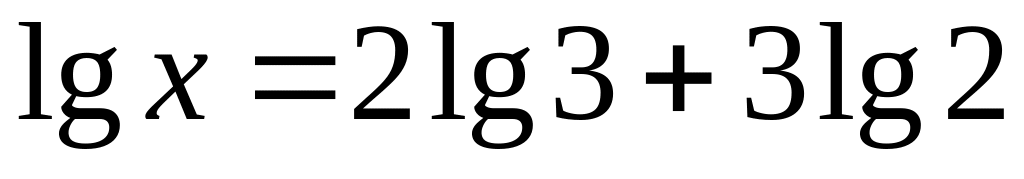 ;
3)
;
3)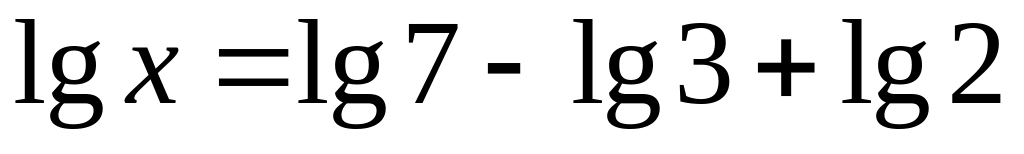 ;
4)
;
4)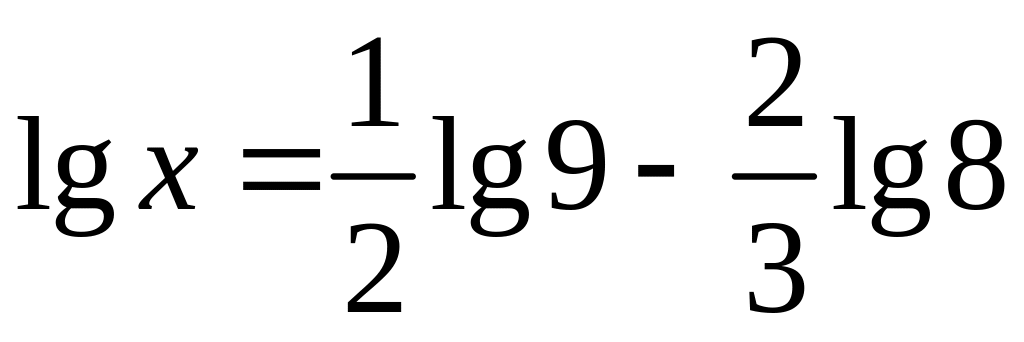 ;
5)
;
5)
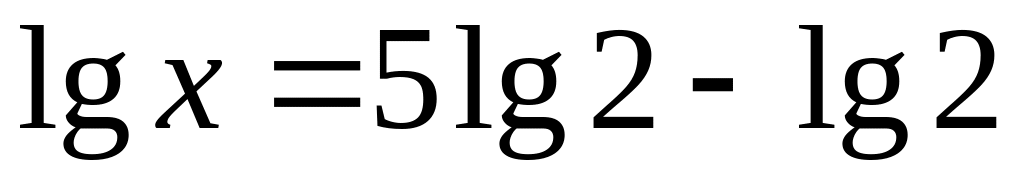 ;
;
6)
![]() .
.
Практическая работа № 6. Решение логарифмических уравнений и неравенств.
Цель: отработать методы решения основных видов логарифмических уравнений и неравенств.
Методические указания.
Уравнение, содержащее
переменную под знаком логарифма,
называется логарифмическим. Простейшим
примером логарифмического уравнения
служит уравнение
![]()
Решение
логарифмического уравнения вида
![]() основано на том, что такое уравнение
равносильно уравнению
при дополнительных условиях
основано на том, что такое уравнение
равносильно уравнению
при дополнительных условиях
![]() .
.
Переход от уравнения
![]() к уравнению
иногда приводит к появлению посторонних
корней. Такие корни можно выявить с
помощью подстановки найденных корней
в исходное логарифмическое уравнение,
либо с помощью нахождения области
определения исходного уравнения (эта
область задается системой неравенств
).
к уравнению
иногда приводит к появлению посторонних
корней. Такие корни можно выявить с
помощью подстановки найденных корней
в исходное логарифмическое уравнение,
либо с помощью нахождения области
определения исходного уравнения (эта
область задается системой неравенств
).
При решении логарифмических уравнений часто бывает полезен метод введения новой переменной.
При решении уравнений, содержащих переменную и в основании, и в показателе степени, используется метод логарифмирования. Если при этом в показателе степени содержится логарифм, то обе части уравнения надо прологарифмировать по основанию этого логарифма.
Неравенство, содержащее переменную под знаком логарифма, называется логарифмическим.
Неравенство,
![]() равносильно системе
равносильно системе
![]() при
при
![]() и
системе
и
системе
![]() при
при
![]() .
.
При решении логарифмических неравенств следует учитывать общие свойства неравенств, свойство монотонности логарифмической функции и область ее определения.
Пример 1. Решить
уравнение
![]() .
.
Решение:
Используя
определение логарифма, получим
![]()
![]() Проверка: при х=1
Проверка: при х=1
![]() или 2=2. Ответ: 21.
или 2=2. Ответ: 21.
Пример 2. Решить
уравнение
![]() .
.
Решение:
Учитывая,
что
![]() и используя свойства логарифмов, получим
и используя свойства логарифмов, получим
![]() .Последнее
уравнение равносильно уравнению
.Последнее
уравнение равносильно уравнению
![]() ,
откуда
,
откуда
![]() .
Проверкой убеждаемся, что
.
Проверкой убеждаемся, что
![]() -
посторонний корень. Ответ: 4.
-
посторонний корень. Ответ: 4.
Пример
3. Решить
уравнение
![]() .
.
Решение:
учитывая,
что
![]() .
Исходное уравнение равносильно следующему
.
Исходное уравнение равносильно следующему
![]() или
или
![]() .
Решая квадратное уравнение относительно
.
Решая квадратное уравнение относительно
![]() ,
получим
,
получим
![]() или
или
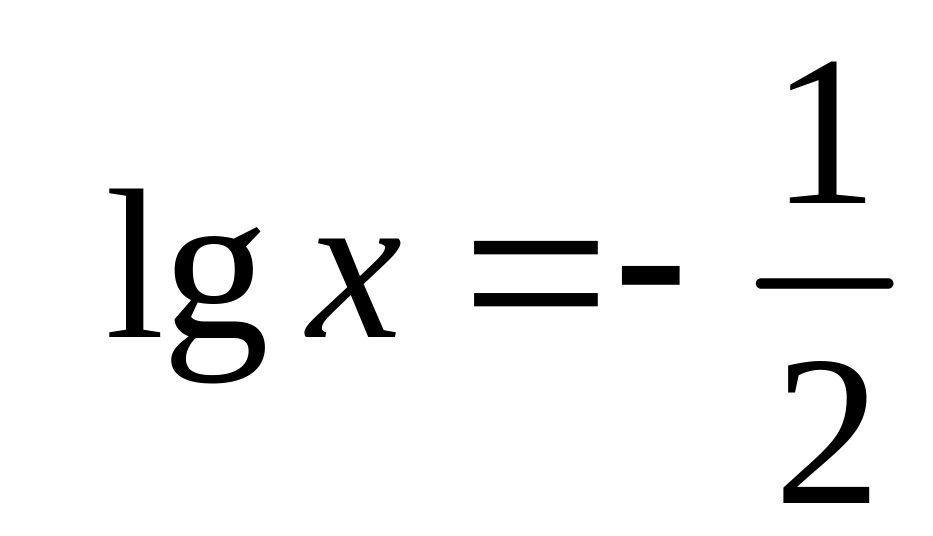 .
Откуда
.
Откуда![]() Проверкой убеждаемся, что
Проверкой убеждаемся, что
![]() -
посторонний корень. Ответ: 10.
-
посторонний корень. Ответ: 10.
Пример
4. Решить
уравнение
![]() .
.
Решение:
прологарифмируем
обе части уравнения по основанию 10,
получим
![]() .
Преобразовываем последнее уравнение
по свойствам логарифмов, получим
.
Преобразовываем последнее уравнение
по свойствам логарифмов, получим
![]() .
Решая квадратное уравнение относительно
,
получим
.
Решая квадратное уравнение относительно
,
получим
![]() или
или
![]() .
Откуда
.
Откуда
![]() .
Ответ: 100, 0,1.
.
Ответ: 100, 0,1.
Пример 5. Решить
неравенство
![]() .
.
Решение:
число -2
равно
![]() .
Поэтому данное неравенство можно
переписать в виде
.
Поэтому данное неравенство можно
переписать в виде
![]() .
Логарифмическая функция с основанием
.
Логарифмическая функция с основанием
![]() определена и убывает на
определена и убывает на
![]() ,
так как
.
Следовательно, последнему логарифмическому
неравенству удовлетворяют такие числа
х, для которых выполнено условие
,
так как
.
Следовательно, последнему логарифмическому
неравенству удовлетворяют такие числа
х, для которых выполнено условие
![]() ,
откуда
,
откуда
![]() .
Ответ:
.
Ответ:
![]() .
.
Пример 6. Решить
неравенство
![]() .
.
Решение: данное неравенство равносильно системе
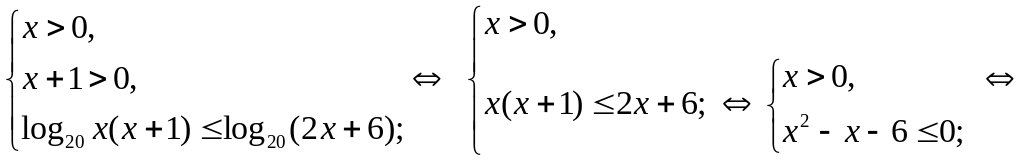
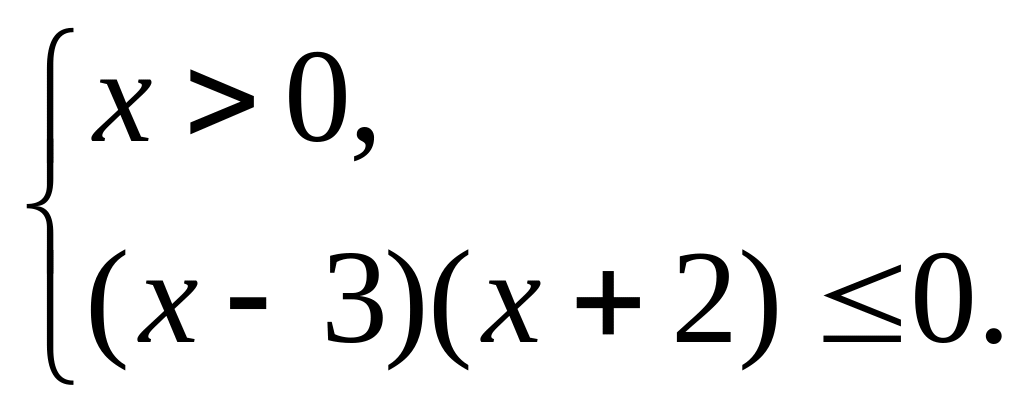
Решением последней
системы является промежуток![]() .
Ответ:
.
Ответ:
![]() .
.
УПРАЖНЕНИЯ.
1. Решить уравнения:
1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() ;
6)
;
6)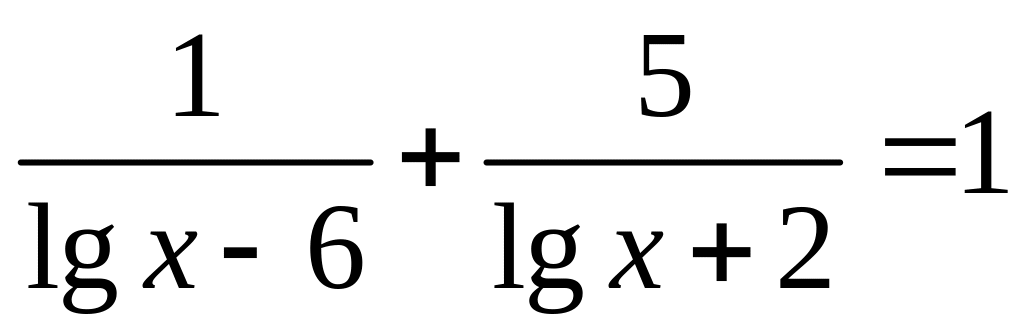 .
.
2. Решить неравенство:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ.
Решить уравнение:
1)![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() ;
9)
;
9)
![]() ;
10)
;
10)
![]() .
.
Практическая работа № 7.
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ.
Цель: отработать определения и основные свойства тригонометрических функций, методы преобразования логарифмических выражений с помощью основных формул тригонометрии.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ.
Рассмотрим единичную
окружность, то есть окружность с центром
О и радиусом, равным 1. На единичной
окружности отметим точку
![]() .
При повороте начального радиуса около
центра О на угол
.
При повороте начального радиуса около
центра О на угол
![]() радиан точка
перейдет
в некоторую точку
радиан точка
перейдет
в некоторую точку
![]() .
.
Синусом угла
![]() называется отношение ординаты точки к
радиусу окружности, то есть
называется отношение ординаты точки к
радиусу окружности, то есть
![]() .
.
Косинусом угла
называется отношение абсциссы точки к
радиусу окружности, то есть
![]() .
.
Тангенсом угла
называется отношение ординаты точки к
ее абсциссе, то есть
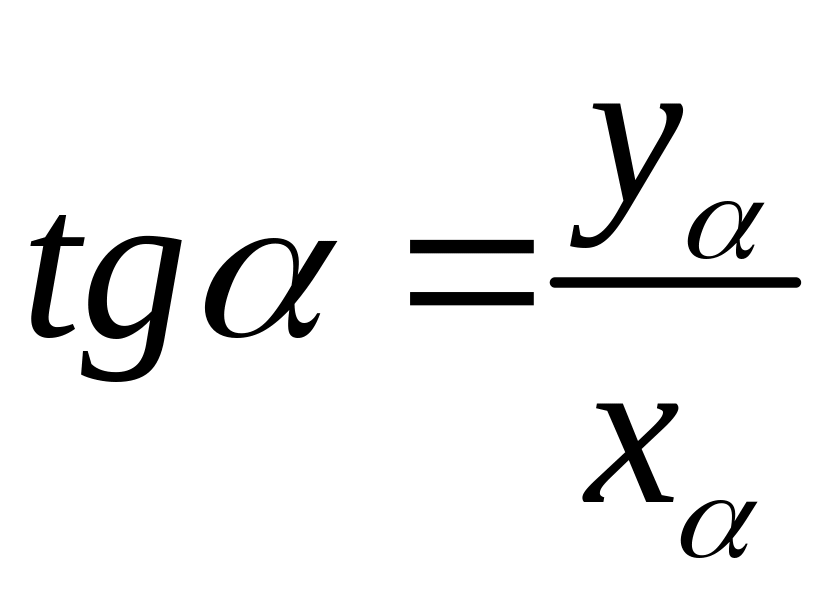 .
.
Котангенсом угла
называется отношение абсциссы точки к
ее ординате, то есть
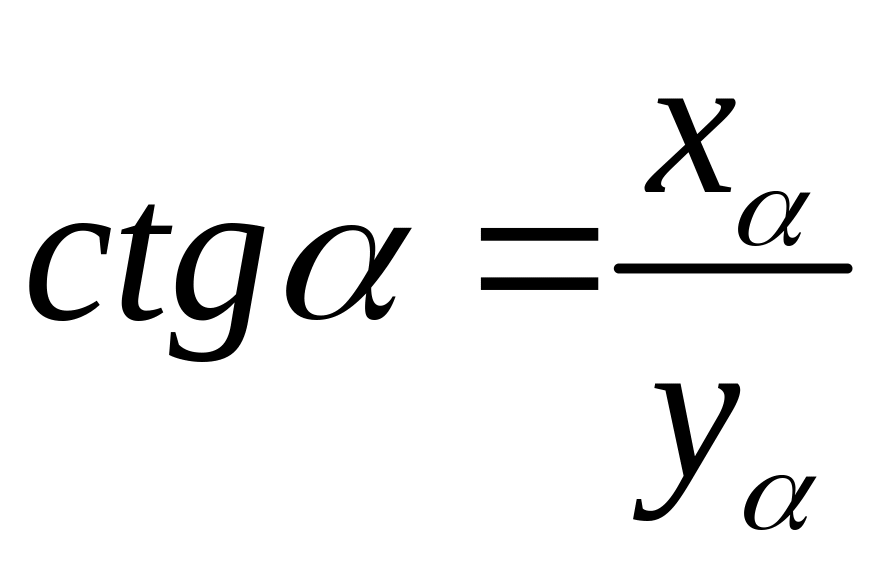 .
.
Знаки значений синуса, косинуса, тангенса и котангенса.
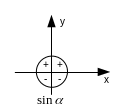
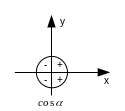
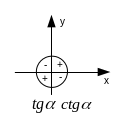
Основные тригонометрические тождества.
1.
![]() .
2.
.
2.
![]() .
.
3.
![]() .
4.
.
4.
![]() .
.
5.
![]() .
6.
.
6.
![]() .
.
Формулы сложения двух аргументов тригонометрических функций.
![]()
![]()
![]()
![]()
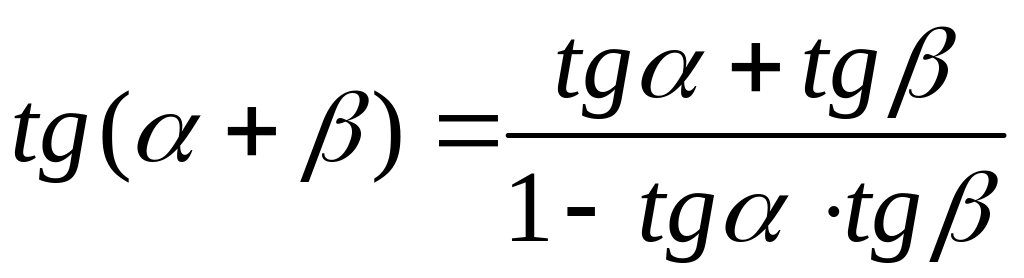
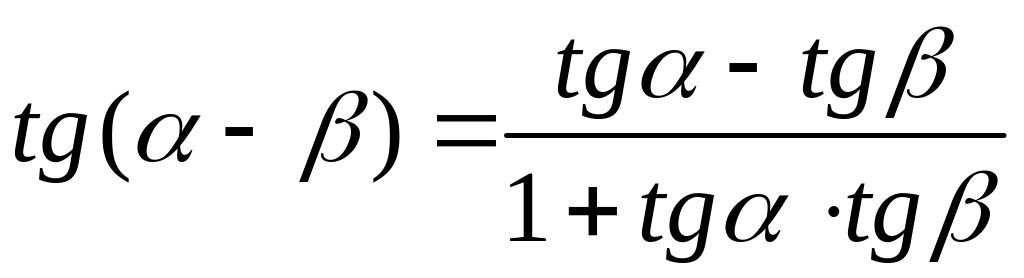
Формулы суммы и разности синусов и косинусов.
![]()
![]()
![]()
![]()
Формулы двойного аргумента.
![]()
![]()
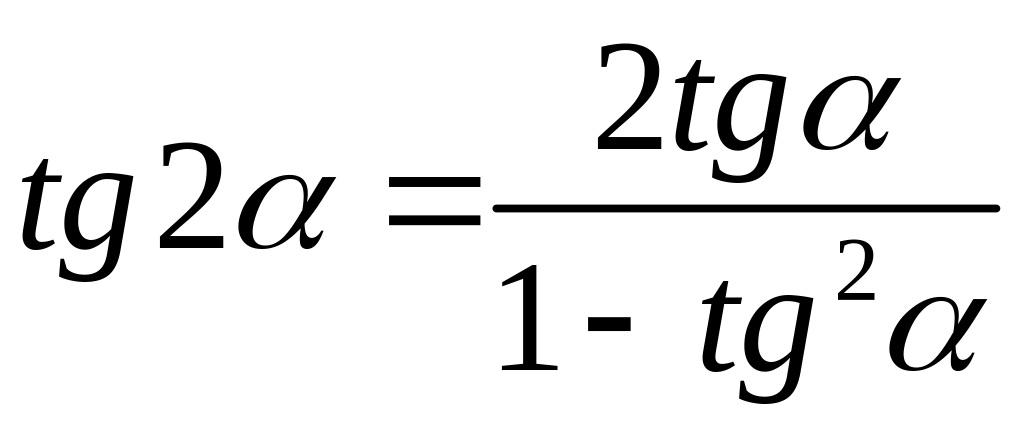
Формулами приведения
называются соотношения, с помощью
которых значения тригонометрических
функций аргументов
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
выражаются через значения
,
выражаются через значения
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Для запоминания этих формул удобно пользоваться следующим правилом:
при переходе от функций углов , к функции угла название функции изменяется: синус на косинус, тангенс на котангенс и наоборот;
при переходе от функций углов , к функции угла название функции не изменяется.
считая острым углом (
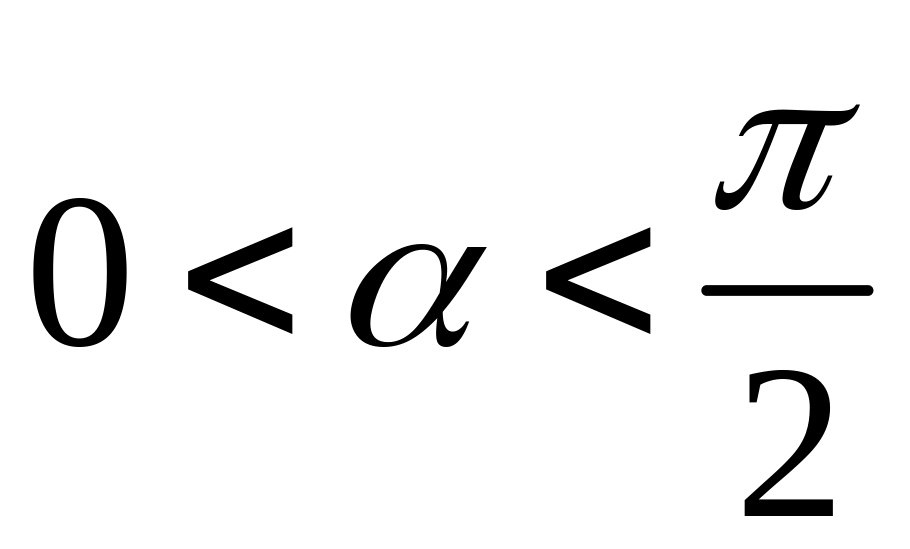 )
перед функцией угла
ставят знак, какой имеет приводимая
функция.
)
перед функцией угла
ставят знак, какой имеет приводимая
функция.
Пример 1. Вычислить
значение
,
если
![]() ,
,
![]() .
.
Решение:
из основного
тригонометрического тождества
,
![]() ,
,
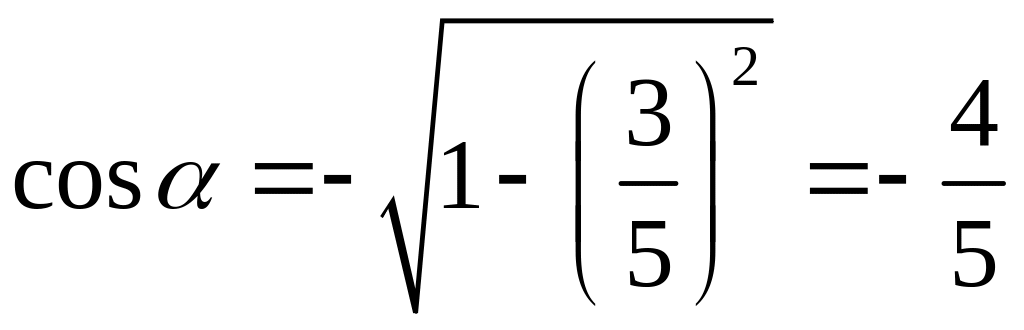 (перед радикалом стоит знак «минус»,
так как во II
четверти
(перед радикалом стоит знак «минус»,
так как во II
четверти![]() ).
).
Пример 2.
Определить знак выражения
![]() .
.
Решение:![]() так как 3650
– угол I
четверти, в которой
положителен, аналогично
так как 3650
– угол I
четверти, в которой
положителен, аналогично
![]() (I
четверть),
(I
четверть),
![]() (III
четверть),
(III
четверть),
![]() (IV
четверть),
(IV
четверть),
![]() (IV
четверть).
(IV
четверть).
Пример 3.
Упростить выражение
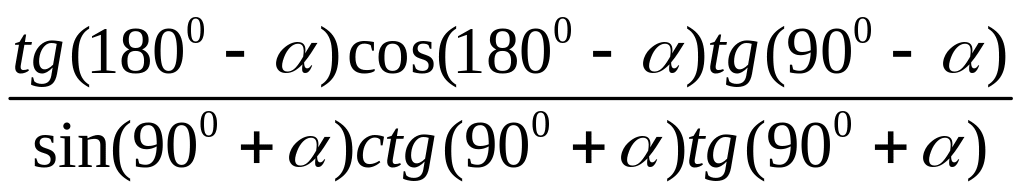 .
Решение:
используя
формулы приведения, получим
.
Решение:
используя
формулы приведения, получим
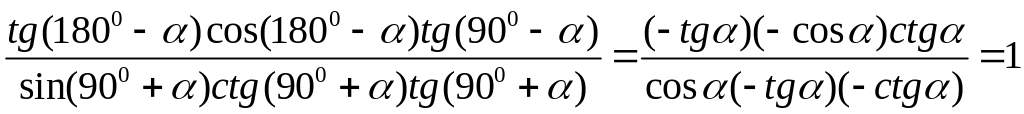 .
.
Пример 4.
Упростить выражение
![]() .
.
Решение:
используя
основные тригонометрические тождества,
получим
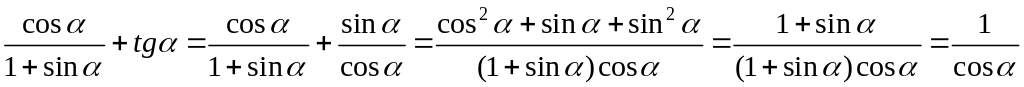 .
.
