Упражнения.

1) Построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, K (рис. 6).

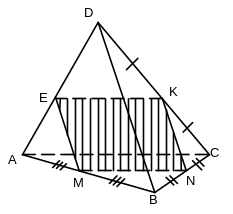
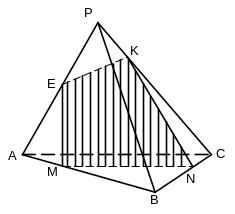
Рис. 6 Рис. 7

2) Построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, K; NM || AC (рис. 7).

3) Построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, K. EKNM – искомое сечение (рис. 8).

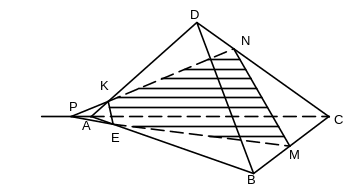
Рис. 8

4) Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его ребер (рис. 5).

5) Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся вершинами куба. Найти периметр сечения, если ребро куба равно (рис. 6).

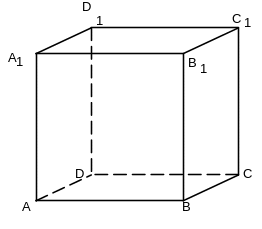
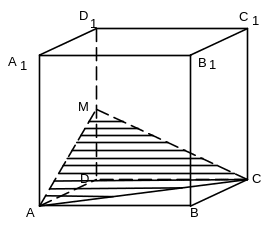
Рис. 6 Рис. 7

6) Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся либо вершинами куба, либо серединами его ребер. (рис. 7).

7) Даны тетраэдр SABC и точки M и N, причем точка М лежит на ребре SC, а точка N – на ребре АВ. Постройте пересечение плоскостей ABM и SCN.

8) Дан куб ABCDA₁B₁C₁D₁, причем К лежит на ребре АА₁, L – на ребре СС₁ и М – на ребре DC. Постройте сечение куба плоскостью, проходящей через точки К, L, М.

9) В тетраэдре SABC постройте сечение плоскостью, проходящей через три точки, лежащие на ребрах SA, АС и ВС.

10) В тетраэдре SABC постройте сечение плоскостью, проходящей через вершину S и точки М и N, лежащие соответственно на ребрах АВ и АС.

Литература.

1. Апаносов П. Т., Орлов М. И. Сборник задач по математике. – М.: Высшая школа, 1987.

2. Атанасян Л. С. Геометрия. – М.: Просвещение, 2005.Математика для техникумов. Алгебра и начала анализа./ Под. Ред. Г. Н. Яковлева, Ч. 1. – М.: Наука, 1987.

3. Богомолов Н. В. Математика. – М.: Дрофа, 2005

4. Богомолов Н. В.Сборник задач по математике. – М.: Дрофа, 2005.

5. Математика для техникумов. Геометрия./Под. Ред. Г. Н. Яковлева, Ч. 1. – М.: Наука, 1987.

6. Математика для техникумов. Алгебра и начала анализа./ Под. Ред. Г. Н. Яковлева, Ч. 1. – М.: Наука, 1987.

7. Погорелов А. В. Геометрия. – М.: Просвещение, 1990.

85