14.Виды графиков

--По способу построения графики делятся на:

Диаграммы Это графики количественных отношений. Диаграммы применяются для наглядного сопоставления в различных аспектах (пространственном, временном и др.) независимых друг от друга величин: территорий, населения и т.д. При этом сравнение совокупностей производится по какому-либо существенному варьирующему признаку.

Линейные-Они чаще всего используются для изображения динамических рядов и при изучении связи между явлениями.

При изображении состава, структуры того или иного явления нередко используют секторные диаграммы.

Столбиковые диаграммы применяются для изображения динамики или структуры.

Ленточную диаграмму используют для сравнения, а также для характеристики отдельных частей совокупности.

Статистические карты - графики количественного распределения по поверхности. представляют собой условные изображения статистических данных на контурной географической карте, т.е. показывают пространственное размещение или пространственную распространенность статистических данных.

--По форме графич образа.

-Линейные –плоскостные –объемные –фигурные –фоновые

--По цели использования

-для хар-ки структуры -для сравнения –оценки динамики –хар-ки вариации –оценки взаимосвязей

15.Статистические ряды распределения представляют собой упорядоченное распределение единиц данной совокупности на группы по определенному варьирующему признаку. Ряд распределения характеризует структуру или состав изучаемого явления, а также позволяется рассматривать однородные совокупности и закономерности, распределения границ и признаков явлений.

-Если ряд построен по атрибутивным, качественным признакам, то он назначается атрибутивным. (распределение населения по полу, занятости и т.д. )

-Ряд распределения построен по количественному признаку называется вариационным. (распределение работников фирмы по стажу работы). Вариационные ряды могут быть построены в порядке возрастания или убывания. Они также имеют следующие характеристики.

Варианта (признак) – x; Частота (вес) – f; Частоть

Частота или вес показывает, сколько таких признаков (вариант) находится в данной совокупности, т.е. как часто встречается данный признак в совокупности.

з/п в размере 300-400 руб. получают 3 человека.

Частоть – это показатели относительных величин, т.е. это проценты или доли в совокупности.

Вариационные ряды в зависимости от характера вариации (признака) делятся на дискретные и непрерывные.

Ряд распределения может быть:

-ранжированный ряд (возрастающий или убывающий),

-дискретный (варианты имеют значения целых чисел. число членов семьи - 2,3, 4,5 и т.д.)

-интервальный (значения вариант даются в виде интервалов. размер зарплаты 100-200, 200-300 и т.д.)

16.Построение рядов

1. интервальные ряды – это таблица состоящая из 2-х граф(сток) интервалов признака вариация которого изучается и число ед совокупности попадающих в данный интервал или долей этого числа от общей числ-ти сов-ти.

2. дискретные ряды – это таблица состоящая из 2-х граф(или строк): конкретных значений варьирующего признака(вариант) и числа единиц сов-ти с данным значением признака(частот) или долей этого числа от общей чист-ти сов-ти (частностей).

Ряды распред-ния графически можно изобразить при помощи полигона, гистограммы и кумуляты. На оси абсцисс отклад-тся зн-ния вариантов, на оси ординат значения частот или частостей. Дискрет.ряд на графике изображается в виде полигона распред-ния в форме кривой. Интервал.ряд грф-ки изобр-тся в виде гистограммы. Гистограмма может быть преобразована в полигон распр-ния, для чего середины верхних сторон прямоугольников соединяются отрезками прямых.

17.Абсолютные величины – это суммарные обобщающие показатели, характеризующие размеры, объемы и уровни общественных явлений в конкретных условиях места и времени. Такие как ВВП, ВНП, Различают два вида абсолютных величин:

-индивидуальные (характеризуют размеры признака у отдельных единиц совокупности). Например, стипендии отдельного студента, Индивидуальные получают непосредственно в результате статистического наблюдения;

-Суммарные (характеризуют итоговое значение признака по определенной изучаемой совокупности).

Абсолютные статистические показатели представляют собой именованные величины, т.е. имеют определенную единицу измерения. В зависимости от сущности исследования абсолютные величины делятся на: Натуральные; Условно-натуральные; Стоимостные; Трудовые.

Натуральные абсолютные величины выражены в тонах, литрах, килограммах, т.е. являются простыми. Условно-натуральные выражаются в пересчете определенных показателей. Например, в топливной промышленности топливо пересчитывается в условное топливо.

Стоимостные – денежные единицы измерения. Трудовые измерители (человеко/дни, человека/ч) учитывают общие затраты производительности труда на предприятиях.

18.Относительная величина – это обобщающий показатель, полученный в результате сравнения двух абсолютных величин. Величина, с которой сравнивают (знаменатель) называется базой сравнения (основание), а сравниваемая величина (числитель) называется текущей (отчетной) пок-тель.

Относительные величина в зависимости от базы сравнения могут быть выражены в:

• Коэффициентах;

• Процентах (если база сравнения равна 100);

• Промилях (если база сравнения равна 1000);

• Именованных величинах (человек/км²

По своему содержанию относительные величины делятся на виды:

1. относительная величина прогноза (% выполнения плана)

2. Относительная величина структуры

3. Относительная величина динамики

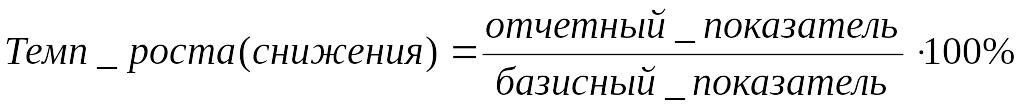
4. Относительная величина сравнения: сравнивается одноименные показатели в различных территорий и объектов (например, добыча угля).

5. Относительная величина интенсивности: здесь сравниваются разноименные показатели в разрезе различных территорий и объектов. Это всегда именованная величина (например, потребление продуктов питания на душу населения);

6. Относительная величина координации (соотношение отдельных частей целого между собой,).

Относительная величина динамики используется для характеристики изменения явления во времени. Вычисляются путем отношения величины текущего периода к величине одного из прошлых периодов. Расчет показателей с постоянной и переменной базой.

ОВД= текущей показатель \ предыдущей (или базиный) показатель

Базисные-сравнение осущь с одним и тем-же базисным уровнем (первым годом)

Цепные –сравнение осуществляется с предыдущем уровнем

19.Средняя величина – это обобщающий показатель, характеризующий однотипные общественные явления по одному количественному признаку в конкретных условиях места и времени. Например, средняя продолжительность жизни. Первым условием применения средних величин является тот факт, что все средние должны опираться на массовые общественные явления. Вторым условием применения средних является тот факт, что групповые средние должны дополняться общими средними (ср. урожайность пшеницы в области и средняя в РФ). Третьим условием является то, что все показатели средних должны определяться по однородной совокупности.

Виды: степенные, структурные. Выбор зависит от цели исследования, экон сущности, хар-ра данных

Средняя арифметическая простая равна сумме показателей (уровней), деленной на число показателей (уровней).

Средняя арифметическая взвешенная принимается в тех случаях, когда известны отдельные значения признака и их веса (fi), т.е. частота повторения признака.

Средняя арифметическая взвешенная равна сумме произведений признака на вес, деленной на сумму веса.

Если показатель в виде интервала то необходимо определить середину интервала по средней арифметической простой, а затем производить последующий расчет.

21.Основные свойства средней арифметической.

1. Если из всех вариантов ряда вычесть или ко всем вариантам добавить постоянное число, то средняя арифметическая соответственно уменьшится или увеличится на это число. .

2. Если все варианты ряда умножить или разделить на постоянное число, то средняя арифметическая соответственно увеличится или уменьшится в это число раз. .

3. Если все частоты увеличить или уменьшить в постоянное число раз, то средняя от этого не изменится. .

4. Сумма отклонений всех вариантов ряда от средней арифметической равна 0. (Нулевое свойство средней). .

5. Общая средняя совокупности равна средней арифметической из частных средне взвешенных по объемам частных совокупностей. , где - средняя арифметическая частных групп, - численность соответствующих групп, - общая средняя.

6. Сумма квадратов отклонений всех вариантов ряда от средней арифметической меньше суммы квадратов их отклонений от любого другого постоянного числа.

7. 

Средний квадрат отклонений вариантов ряда от произвольного числа А равен дисперсии плюс квадрат разности между средней и этим числом А