1.3. Корені многочленів

Нехай задано многочлен .

Означення. Число називають коренем многочлена ), якщо

.

Теорема Безу. Остача від ділення многочлена на многочлен спеціального вигляду дорівнює числу .

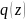Доведення. Застосуємо теорему про ділення многочлена з остачею до многочленів та Тоді існують такі та , що

, ,

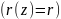причому або або степінь менший за степінь многочлена .

Підставимо в попередню рівність :

.

Наслідок. Для того щоб число було коренем многочлена , необхідно й достатньо, щоб ділився на без остачі.

Доведення. Необхідність.

Нехай корінь многочлена , тобто . Застосуємо до і теорему про ділення з остачею. За теоремою Безу 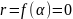. Отже, ділиться на без остачі.

Достатність доведіть самостійно.

У зв’язку з тим, що пошук коренів пов’язаний з теорією подільності, виникає питання найбільш оптимального ділення многочлена на многочлен . Для цього опишемо і обґрунтуємо схему ділення,яку називають схемою Горнера.

Задамо . Поділимо на .

Нехай

Треба знайти числа та r. Для цього порівняємо в останній рівності коефіцієнти за рівних степенів z:

……………………………………………………………………………………….

Результати подамо як схему Горнера:

				…
				…

За схемою Горнера можна розв’язувати такі задачі:

1) ділення (знайти частку і остачу) многочлена на ;

2) знаходження значення многочлена при ;

3) пошук значення похідних без знаходження їх самих;

4) випробовування чисел на корені;

5) знаходження кратності кореня;

6) розкладання многочлена за формулою Тейлора.

Розглянемо поняття k-кратного кореня многочлена.

Означення. Число α називають k-кратним коренем многочлена , якщо ділиться на і не ділиться на .

Щоб отримати умову існування k-кратного кореня, треба знати поняття похідної від многочлена.

Многочлен являє собою комплексну функцію комплексної змінної, оскільки змінна і коефіцієнти при степенях – комплексні числа. Хоча формально поняття границі для комплексної функції комплексної змінної не відрізняється від поняття границі для дійсної функції, фактично воно стає більш жорстким. Це пов’язано з тим, що околом точки для дійсної змінної є інтервал, а околом у комплексній області є відкритий круг. Тому ми не можемо використати знання з математичного аналізу за перший курс. Зважаючи на це введемо поняття похідної многочлена (воно узгоджується з відповідними поняттями функції комплексної змінної).

Означення. Похідною многочлена називають многочлен .

Виходячи з означення похідної для многочлена можна довести такі правила знаходження похідної:

1) .

2) .

3)

Теорема. Нехай α – k-кратний корінь многочлена Тоді α є корінь кратності k-1 для його похідної

Доведення. Припустимо, що α – k-кратний корінь, тоді

Потрібно довести, що

і .

Виходячи з правил обчислення похідних маємо

.

Це означає, що

Залишилося довести, що .

Позначимо

Припустимо супротивне:

Тоді .

За припущенням , тоді і , а це суперечить тому, що не . Маємо суперечність. Теорему доведено.