79

Передмова

У даному виданні уміщено матеріал із алгебри та геометрії, обов’язковий для студентів факультету прикладної математики. Виклад курсу побудовано таким чином, що формалізовані алгебричні поняття набувають геометричної інтерпретації.

Перший розділ присвячено многочленам. Це питання належить до перших, найдавніших задач алгебри, яку розглядали як науку про розв’язування алгебричних рівнянь. У цьому розділі встановлено зв’язок між теорією подільності і коренями многочлена. Наведено основну теорему алгебри і наслідків з неї, властивості коренів многочленів із дійсними коефіцієнтами.

Для того щоб перейти до геометричної інтерпретації многочленів від двох і трьох змінних, у другому розділі уміщено додаткову інформацію про лінійні простори, розглянуто узагальнення понять лінійного простору, координат вектора та їх перетворень. Далі ці абстрактні поняття набувають геометричної інтерпретації в тривимірному і двовимірному геометричному просторі.

У третьому розділі конспекту лекцій описано різні способи задання ліній і поверхонь на площині та в просторі. Особливу увагу приділено алгебричним лініям, порядок яких не змінюється в разі переходу до іншого базису.

У четвертому розділі охарактеризовано алгебричні лінії і поверхні першого порядку. Доведено, що їх геометричними образами є прямі та площини. Розглянуто також умови паралельності й збіжності прямих і площин.

У п’ятому розділі описано геометричні образи многочленів другого порядку від двох змінних, побудовано загальну теорію кривих другого порядку.

Розділ шостий можна вважати вступом до сучасної алгебри. У межах понять ХІХ ст. не можна було з’ясувати основне питання тодішньої алгебри – умов існування коренів алгебричного рівняння. Потрібні були нові поняття і підходи. Алгебра перестала бути наукою про алгебричні рівняння.

Сучасна алгебра – це наука, про алгебричні структури. У шостому розділі розглянуто елементи сучасної алгебри (групи, кільця, поля).

Теорію лінійних операторів, евклідів простір описано в сьомому, дев’ятому, десятому розділах.

Білінійним і квадратичним формам та їх застосуванню присвячено восьмий і десятий розділи.

1. Теорія многочленів

1.1. Поняття многочлена, алгебра многочленів

Існують два погляди на поняття многочлена: формально-алгебричний і теоретико-функціональний.

Означення (формально-алгебричне). Многочленом відносно змінної z називають суму цілих невід’ємних степенів z, взятих з деякими коефіцієнтами.

Означення (теоретико-функціональне). Многочлен – це функція спеціального вигляду:

Змінну z і коефіцієнти вважатимемо комплексними. Найбільш поширені такі форми запису многочлена:

– за зростаючими степенями;

– за спадними степенями.

Означення. Степенем многочлена називають найвищий показник, із яким z входить до многочлена з коефіцієнтом, який не дорівнює 0.

Над многочленами здійснюють дві основні алгебричні операції: додавання і множення. Застосуємо форму запису многочлена за зростаючими степенями.

Означення. Сумою многочленів і називають многочлен із коефіцієнтами такими, що .

Означення. Добутком і 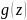називають многочлен , коефіцієнти якого обчислюють за таким правилом: . Із цього правила випливає правило множення многочленів як двох сум.

Означення (формально-алгебричне). Два многочлени називають рівними, якщо вони мають однакові коефіцієнти при однакових степенях z.

Означення (теоретико-функціональне). Дві функції (у тому числі й многочлен) називають рівними, якщо: 1) у них однакові області визначення; 2) за однакових значень аргументу вони набувають однакових значень.

Властивості операцій:

1) – комутативність додавання;

2) – асоціативність додавання;

3) – комутативність множення;

4) – асоціативність множення;

5) – дистрибутивність.

Зрозуміло, якщо многочлени рівні у формально-алгебричному сенсі, то рівні вони і в теоретико-функціональному. Обернене не очевидно. Ми доведемо цей факт пізніше, застосувавши наслідок основної теореми.

З’ясуємо питання про існування операцій, обернених додаванню і множенню. Для цього застосуємо поняття оберненої операції до загальної внутрішньої операції .

Візьмемо за операцію операцію додавання: . Встановимо, чи існує для заданих й 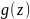такий многочлен , що . Позначимо 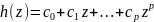. Тоді . Звідси . Отже, такий многочлен існує.

Візьмемо за операцію операцію множення: . Доведемо, що для множення не існує оберненої операції. Проаналізувавши поняття оберненої операції, дійдемо висновку, що для цього достатньо навести принаймні одну пару многочленів й , для яких не існує такого многочлена , щоб . Такими, наприклад, є , . Але не многочлен. Отже, обернена множенню операція невизначена в множині многочленів.