
- •Рецензент: хоробров в.Р., доцент
- •Введение
- •Алгоритмизация
- •1. Вычисление суммы (суммирование) элементов вектора
- •2. Вычисление произведения элементов вектора
- •Пример 3
- •3. Вычисление произведения двух векторов
- •4. Суммирование (вычитание) матриц
- •5. ВычислениЕ произведения матриц
- •6. Вычисление произведения матрицы на вектор
- •7. Вычисление единичной матрицы
- •8. Транспонирование матрицы
- •A ij пустая ячейка b aji
- •9. Инвертирование элементов вектора
- •10. Алгоритм поиска максимального ( или минималь-ного ) элемента вектора
- •11. Алгоритм сортировки (упорядочивания) элементов вектора или матрицы
- •12. Вычисление полинома по схеме горнера
- •13. Вычисление суммы членов ряда
- •С одержание
4. Суммирование (вычитание) матриц
C = A + B =
j = 1, 2, . . . , N. ( 10 ) |
Рис. 14 |
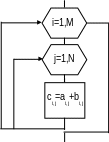
Алгоритм суммирования матриц показан на рис. 14.
Алгоритм вычитания матриц аналогичен рассмотренному, за исключе-нием очевидной замены знака " + " на " - ".
5. ВычислениЕ произведения матриц
Даны две прямоугольные
матрицы A={
}N*M
и B={![]() }M*K
.
}M*K
.
В результате
вычисления произведения матриц A
и B
получим
прямоугольную матрицу C={
![]() }N*K
, в которой
число строк равно числу строк матрицы
A
(т.e.
N),
а число столбцов - числу столбцов матрицы
B
(т.e.
K).
Отметим, что число столбцов матрицы A
равно числу
строк матрицы B
(т.e.
M).
}N*K
, в которой
число строк равно числу строк матрицы
A
(т.e.
N),
а число столбцов - числу столбцов матрицы
B
(т.e.
K).
Отметим, что число столбцов матрицы A
равно числу
строк матрицы B
(т.e.
M).
Например,
C = A*B
= *
* =
= (
11 )
(
11 )
для
Алгоритм для вычисления произведения двух прямоуголь-ных матриц показан на рис. 15. Отметим, что в результате вычисления произведения двух квадратных матриц размерностью (N*N) получим квадратную матрицу такой же размерности.
|
Рис.15 |
6. Вычисление произведения матрицы на вектор
Даны прямоугольная
матрица A={
}N*M
и вектор B={![]() }M
.
}M
.
В результате вычисления произведения матрицы A и вектора B получим вектор C , в котором число элементов равно числу строк матрицы A (т.е. N). Отметим, что число элементов вектора B равно числу столбцов матрицы A (т.e. M).
Формализация данной задачи приводит к следующему выраже-нию:
для
Алгоритм вычисления произве-дения матрицы на вектор показан на рис. 16. |
Рис.16 |
7. Вычисление единичной матрицы
Формализация данной задачи приводит к следующему выраже-нию:
E={
для
Алгоритм вычисления единич-ной матрицы приведен на рис. 17.
|
Рис. 17 |

 Данные
действия над двумя матрицами
A
и B
могут быть
произведены, если размерности обоих
матриц равны, предположим (M*N).
Результатом сумми-рования (вычитания)
будет матрица C
такой же
размерности (M*N).
Данные
действия над двумя матрицами
A
и B
могут быть
произведены, если размерности обоих
матриц равны, предположим (M*N).
Результатом сумми-рования (вычитания)
будет матрица C
такой же
размерности (M*N).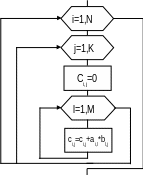 Формализация
данной задачи имеет следующий вид:
Формализация
данной задачи имеет следующий вид: Например,
C
= A*B
=
Например,
C
= A*B
=

