Виды относительных величин.

В зависимости от задач, решаемых с помощью относительных величин, различают несколько их видов.

1. относительная величина планового задания (ОВПЗ)

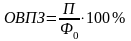
П – устанавливаемый уровень показателя на планируемый период

Ф₀ – показатель предыдущего периода, либо какого-либо другого периода, принятого за базу сравнения

2. относительная величина выполнения плана (ОВВП)

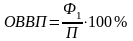
Ф₁ – фактический уровень показателя

3. относительная величина динамики (ОВД)

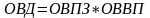
Относительные величины динамики могут быть с постоянной и переменной базой сравнения.

Ряд динамики – годы.

годы	1998	1999	2000	2001	2002	2003	2004
показатель	Y1	Y2	Y3	Y4	Y5	Y6	Y7

Базисные относительные величины (показывают постепенное изменение показателя, база сравнения -постоянная).

ОВД₁=у₂/у₁, ОВД₂=у₃/у_1, ОВД₃=у₄/у₁ и т.д.

Цепные относительные величины динамики (база сравнения переменная, показывают как изменяется величина показателя между двумя соседними периодами времени)

ОВД₁=у₂/у₁, ОВД₂=у₃/у_2, ОВД₃=у₄/у₃ и т.д.

Цепные и базисные ОВД взаимосвязаны между собой:

1. если последующую базисную величину динамики разделить на предыдущую, то получим цепную ОВД.

Пример: у₄/у₁: у₃/у₁= у₄/у₃

2. если перемножить две рядом стоящие цепные ОВД, то получим базисную.

Пример: у₂/у₁∙ у₃/у₂= у₃/у₁

4. относительная величина структуры (ОВС) представляет собой соотношение части и целого

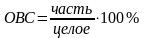
ОВС характеризует структуру, состав той или иной совокупности явлений, а ОВС, вычисленные за ряд лет, являются базой для анализа структурных изменений (сдвигов)

5. относительная величина координации (ОВК) выражает соотношение размеров частей и целого между собой и показывает, сколько единиц одной части приходится на 1/100/100/10000 и т.д. единиц другой его части.

Если целое состоит более, чем из двух частей, то за базу сравнения принимают либо самую маленькую часть целого, либо самую большую часть целого и все остальные части сравнивают с этой базой.

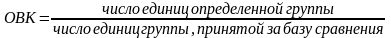
6. относительная величина интенсивности (ОВИ) характеризует степень распространения явления в данной среде. Ее получают в результате соотношения размеров двух качественно различных явлений. Числитель – размер самого явления, знаменатель – объем среды, в которой явление распространяется.

Относятся все демографические коэффициенты.

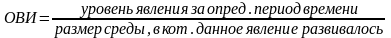
7. относительная величина экономического развития (ОВЭР) (разновидность ОВИ), она характеризует производство продукции на душу населения, эта величина именованная.

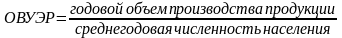
8. относительная величина сравнения представляет собой соотношение величин одноименных показателей, относящихся к разным объектам или к разным территориям. Выражается в коэффициентах и процентах.

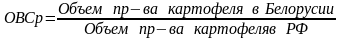
Средние величины

1. Сущность и задачи средних величин.

Средние величины представляют собой наиболее распространенную форму сводных обобщающих показателей. Они дают общую количественную характеристику массового процесса.

Средняя величина отражает средний уровень развития явления, достигнутый к определенному моменту или определенный промежуток времени

Средние представляют значение признаков совокупности в целом одним числом. Они нивелируют индивидуальные различия величин внутри совокупности, т.е. в средних взаимопогашаются случайные отклонения отдельных величин от основного типа. Взаимопогашение происходит в том случае, если берется большая масса явлений, поэтому понятие средней величины связано с законом больших чисел.

Средняя величина правильно характеризует совокупность лишь в том случае, если последняя качественно однородна по изучаемому признаку.

Средние облегчают сравнение показателей в совокупности, обладающих разными численностями. Статистический анализ, который проводится с помощью средних величин, тесно связан с методом группировок.

Средние, вычисленные для отдельной части (группы) изучаемой совокупности называют групповыми (частными) средними. Групповая средняя характеризует типичный размер признака в группе. Совокупности частных средних конкретизируют величину общей средней и дают более детальную характеристику совокупности.

Средняя величина, вычисленная для всей совокупности, называют общей средней. Общая средняя отражает некоторые общие условия, в которых находится разнородная совокупность явлений

2. Виды средних аналитических.

Выбор конкретного виды средней зависит от условий решаемой задачи. При расчете средней величины определяют признак, по которому находят среднее значение. Он называется осредняемым.

Средние величины могут рассчитываться по сгруппированным данным (т.е. по ряду распределения) и по неупорядоченной совокупности. В зависимости от этого различают:

- взвешенные средние;

- невзвешенные (простые) средние.

Все формулы средних аналитических получают из формулы степенной средней.

Формулы средних величин

Взвешенные средние	Простые средние
1. Средняя степенная	1. Средняя степенная
2. Средняя гармоническая (k= –1) агрегатная	2. Средняя гармоническая (k= –1)
3. Средняя геометрическая (k=0)	3. Средняя геометрическая (k=0)
4. Средняя арифметическая (k=1) агрегатная	4. Средняя арифметическая (k=1)
5. Средняя квадратическая k=2	5. Средняя квадратическая k=2

Методика выбора формы средней.

Имеются данные о реализации яблок в килограммах и цене за килограмм яблок в овощных отделах магазинов города:

Номер наблюдения	Цена 1 кг, руб. [x]	Объем реализации, кг в месяц [f]
1	22	300
2	23	400
3	25	350
4	27	200
5	37	400
6	55	250
7	56	300
8	65	250
Итого:		2450

Определить среднюю цену за 1 килограмм яблок.

Логическая формула:

средняя цена товара= выручка (в денежном выражении)/объем реализации (кг.)

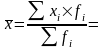=(22·300+23·400+...+65·250)/2450=

37,37(руб.)

Имеются данные о цене за килограмм яблок и выручке от их продажи в овощных отделах магазинов города:

Номер наблюдения	Цена 1 кг, руб. [x]	Объем реализации в денежном выражении (руб.) [x·f]
1	22	6600
2	23	9200
3	25	8750
4	27	5400
5	37	14800
6	55	13750
7	56	16800
8	65	16250
Итого:	-	91550

Логическая формула остается прежней, но изменились исходные данные.

Следовательно, изменится математическая формула.

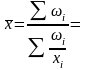
= 91550/(6600/22+9200/23+...+16250/65)=

37,37 (w=x·f)

Имеются данные о выручке и объеме реализации яблок (в килограммах) в овощных отделах магазинов города:

Номер наблюдения	Выручка (руб.) [ ]	Объем реализации, кг [ ]
1	6600	300
2	9200	400
3	8750	350
4	5400	200
5	14800	400
6	13750	250
7	16800	300
8	16250	250
Итого:	91550	2450

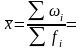
=91550/2450=37,37 (руб.)

Применение средней гармонической

Один рабочий в течение дня затрачивает на изготовление одной детали 2 минуты, второй – 4 минут, третий - 6 минут. Определить средние затраты времени на изготовление одной детали.

Средние затраты времени на 1 деталь = все время/все детали

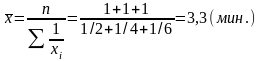
Структурные средние
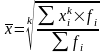
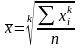
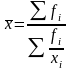
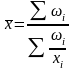
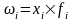
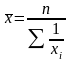
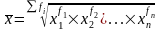
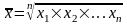
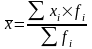
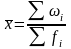
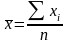
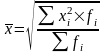
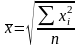
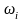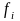