
- •6. ПрактикУм Упражнения и задачи по дисциплине "эконометрика" Упражнения и задачи к теме "Введение в эконометрику"
- •4. Пусть теоретическая ковариация случайных величин и отлична от 0, т.Е. . Имеется набор наблюдений , . Известно также, что .
- •Найти выборочную ковариацию , используя определение и альтернативную формулу для ее вычисления.
- •Найти выборочный коэффициент корреляции .
- •Найти выборочную ковариацию , используя определение и альтернативную формулу для ее вычисления.
- •Найти выборочный коэффициент корреляции .
- •Используя t-критерий, проверить значимость при 5%-ом уровне значимости. Упражнения и задачи к теме "Парный регрессионный анализ"
- •Упражнения и задачи к теме "Множественная линейная регрессия"
- •Упражнения и задачи к теме "Некоторые аспекты построения моделей множественной регрессии"
- •Упражнения и задачи к теме "Проверка выполнимости условий Гаусса-Маркова"
- •Типовые задания для практических занятий по дисциплине "Эконометрика"
- •Методические указания по выполнению работы
- •Вариант № 2
- •Вариант № 3
- •Задание № 2 Изучение явлений гомоскедастичности и гетероскедастичности Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант № 2
- •Вариант №3
- •Вариант № 2
- •Вариант № 3
- •Исходные данные
- •Исходные данные
- •Вариант № 3
- •Исходные данные
- •Задание № 2 Тестирование модели на автокорреляцию остатков Вариант № 1
- •Исходные данные
- •Вариант № 2
- •Исходные данные
- •Вариант № 3
- •Исходные данные
6. ПрактикУм Упражнения и задачи по дисциплине "эконометрика" Упражнения и задачи к теме "Введение в эконометрику"
1. Доказать, что теоретическая ковариация случайных величин обладает следующими свойствами:
 ;
;
 ;
; ;
; где
где
 –
произвольная постоянная;
–
произвольная постоянная; где
–
произвольная постоянная;
где
–
произвольная постоянная; ;
; где
где
 –
произвольные постоянные.
–
произвольные постоянные.
Указание. Для доказательства необходимо использовать свойства математического ожидания и определение дисперсии случайных величин.
2. Доказать, что выборочная ковариация случайных величин обладает следующими свойствами:
 ;
;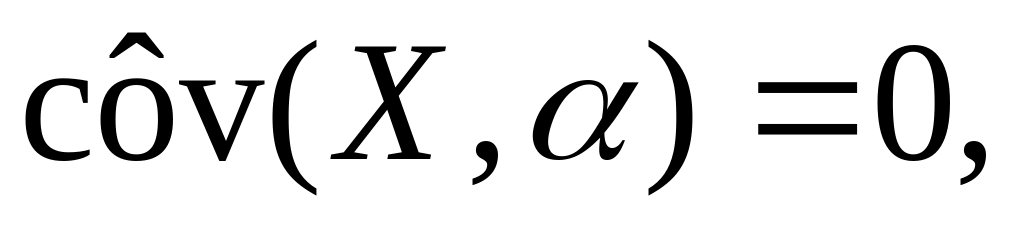 где
где
 –
произвольная постоянная;
–
произвольная постоянная; ;
;
 ,
где
–
произвольная постоянная;
,
где
–
произвольная постоянная; ,
где
–
произвольные постоянные.
,
где
–
произвольные постоянные.
3.
Пусть теоретическая ковариация случайных
величин
![]() и
и
![]() отлична от 0, т.е.
отлична от 0, т.е.
![]() .
Имеется набор наблюдений
.
Имеется набор наблюдений
![]() ,
,
![]() .
Известно также,
что
.
Известно также,
что
![]() .
.
Доказать,
что теоретическая ковариация средних
выборочных
![]() и
и
![]() в
в
![]() раз меньше теоретической ковариации
случайных величин
и
,
т.е.
раз меньше теоретической ковариации
случайных величин
и
,
т.е.
![]() .
.
4. Пусть теоретическая ковариация случайных величин и отлична от 0, т.Е. . Имеется набор наблюдений , . Известно также, что .
Доказать,
что выборочная ковариация случайных
величин
и
является заниженной оценкой теоретической
ковариации этих случайных величин, так
что
![]() .
.
5. Имеются данные по ВВП ( , млрд. у.е.) и доле бюджета страны ( , %), отчисляемой на образование, по 6-ти странам:
|
1 |
2 |
3 |
4 |
6 |
8 |
|
1 |
3 |
9 |
7 |
14 |
14 |
Найти выборочную ковариацию
 ,
используя определение и альтернативную
формулу для ее вычисления.
,
используя определение и альтернативную
формулу для ее вычисления.Найти выборочный коэффициент корреляции
 .
.Используя t-критерий, проверить значимость при 5%-ом уровне значимости.
6. Имеются данные по стажу работы ( , лет) и заработной плате ( , у.е.) 6-ти работников:
|
1 |
3 |
5 |
7 |
8 |
9 |
|
42 |
30 |
21 |
50 |
60 |
49 |
Найти выборочную ковариацию , используя определение и альтернативную формулу для ее вычисления.
Найти выборочный коэффициент корреляции .
Используя t-критерий, проверить значимость при 10%-ом уровне значимости.
7. Имеются следующие данные по группе предприятий о выпуске продукции (Х, тыс. шт.) и себестоимости одного изделия (Y, р.):
|
2,0 |
3,5 |
4,0 |
4,5 |
5,5 |
6,0 |
|
1,9 |
1,7 |
1,8 |
1,6 |
1,5 |
1,4 |
Найти выборочную ковариацию , используя определение и альтернативную формулу для ее вычисления.
Найти выборочный коэффициент корреляции .
Используя t-критерий, проверить значимость при 5%-ом уровне значимости. Упражнения и задачи к теме "Парный регрессионный анализ"
1.
Рассмотрим модель регрессии на константу
![]() .
Пусть в любых двух наблюдениях случайные
компоненты распределены независимо
друг от друга, а дисперсия случайной
компоненты в каждом наблюдении постоянна
и не зависит от номера наблюдения, т.е.
.
Пусть в любых двух наблюдениях случайные
компоненты распределены независимо
друг от друга, а дисперсия случайной
компоненты в каждом наблюдении постоянна
и не зависит от номера наблюдения, т.е.
![]() .
.
Найти по МНК оценку
 параметра
.
параметра
.Найти математическое ожидание
 и дисперсию
и дисперсию .
.Доказать, что

где
![]() - остаток регрессии в i-ом
наблюдении.
- остаток регрессии в i-ом
наблюдении.
Найти
 .
.
2. Рассмотрим
модель регрессии без свободного члена
![]() .
Пусть в любых двух наблюдениях случайные
компоненты распределены независимо
друг от друга, а дисперсия случайной
компоненты в каждом наблюдении постоянна
и не зависит от номера наблюдения, т.е.
.
Пусть в любых двух наблюдениях случайные
компоненты распределены независимо
друг от друга, а дисперсия случайной
компоненты в каждом наблюдении постоянна
и не зависит от номера наблюдения, т.е.
.
Найти по МНК оценку
 параметра
параметра
 .
.Найти математическое ожидание
 и дисперсию
и дисперсию
 .
.Проверить, выполняется ли равенство:
 ,
,
где
![]() -
выборочная средняя расчетных значений
зависимой переменной
;
-
выборочная средняя расчетных значений
зависимой переменной
;
![]() -
расчетное значение зависимой переменной
в
-
расчетное значение зависимой переменной
в
![]() -ом
наблюдении,
-ом
наблюдении,
![]() ;
;
![]() -
выборочная средняя наблюдаемых
значений
.
-
выборочная средняя наблюдаемых
значений
.
Найти сумму квадратов ошибок
 ,
где
,
где
 - остаток регрессии в i-ом
наблюдении,
.
- остаток регрессии в i-ом
наблюдении,
.Найти сумму квадратов регрессии
 .
.Найти полную вариацию зависимой переменной
 .
.Проверить, выполняется ли равенство:
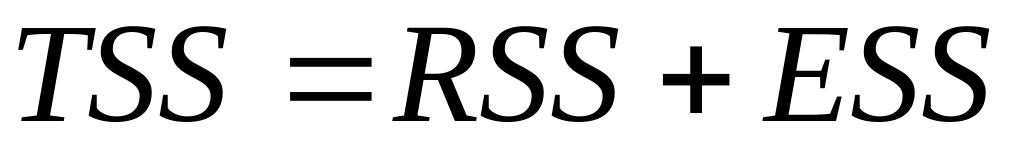 .
.Найти
 ,
,
 ,
,
 .
.
3. Рассмотрим
модель парной линейной регрессии
![]() ,
.
Пусть по выборке объема
найдены МНК-оценки
,
.
Пусть по выборке объема
найдены МНК-оценки
![]() и
и
![]() теоретических коэффициентов регрессии.
теоретических коэффициентов регрессии.
Доказать, что
 ,
где
,
где
 .
.Найти выражение для коэффициентов
 ,
,
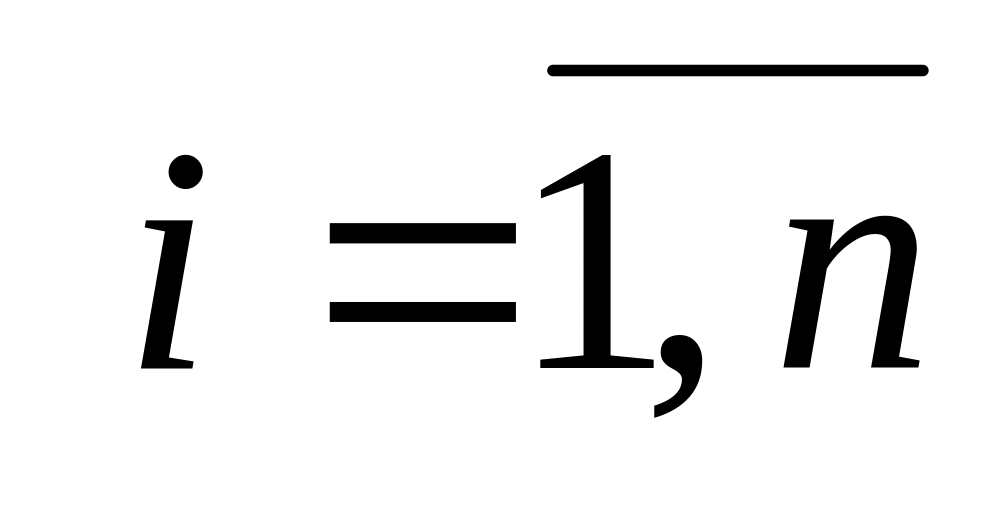 ,
если
,
если
 .
.
4. Пусть , . Проверить справедливость равенств:
 ;
;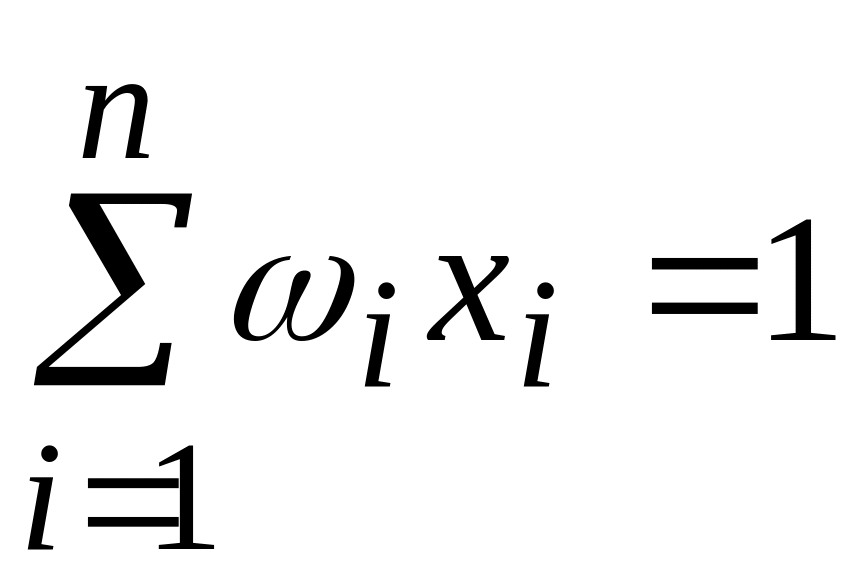 ;
; ;
; .
.
5. Рассмотрим
модель парной линейной регрессии
,
.
Пусть
и
![]() – МНК-оценки параметров
– МНК-оценки параметров
![]() и
и
![]() ,
полученные по выборке объема
,
а случайная компонента
,
полученные по выборке объема
,
а случайная компонента
![]() подчиняется следующим условиям: 1)
подчиняется следующим условиям: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
Доказать, что
 и
и
 .
.Найти теоретическую ковариацию
 .
.Доказать, что
 ,
,
где
;
![]() – расчетное значение переменной
в
-ом
наблюдении,
.
– расчетное значение переменной
в
-ом
наблюдении,
.
Доказать, что
 .
.
6. Рассмотрим модель парной линейной регрессии , . Пусть и – МНК-оценки параметров и , полученные по выборке объема .
Доказать, что ,
где
![]() – выборочная средняя расчетных значений
зависимой переменной
;
– выборочная средняя расчетных значений
зависимой переменной
;
– расчетное значение переменной в -ом наблюдении.
Проверить равенство:

где – остаток регрессии в i-ом наблюдении.
Доказать, что
 .
.
7. Рассмотрим модель парной линейной регрессии , . Пусть случайная компонента подчиняется условиям Гаусса Маркова.
Найти
 ,
,
 и
и
 .
.Проверить, выполняется ли равенство:
 ,
,
где
![]() –
коэффициент
детерминации;
–
коэффициент
детерминации;
![]() –
выборочный
коэффициент
корреляции.
–
выборочный
коэффициент
корреляции.
Проверить, выполняется ли равенство:
 ,
,
где
статистика
![]() имеет распределение Фишера-Снедекора
с
имеет распределение Фишера-Снедекора
с
![]() и
и
![]() степенями свободы;
степенями свободы;
статистика
 имеет распределение Стьюдента с
имеет распределение Стьюдента с
![]() степенями свободы.
степенями свободы.
Проверить, выполняется ли равенство:
 .
.
8. Пусть
для модели парной линейной регрессии
![]() выполняются
все предпосылки МНК;
выполняются
все предпосылки МНК;
![]() – некоторое фиксированное число;
– некоторое фиксированное число;
![]() –
индивидуальное (прогнозное) значение
зависимой переменной, отвечающее
–
индивидуальное (прогнозное) значение
зависимой переменной, отвечающее
![]() ;
;
![]() – расчетное значение зависимой
переменной, отвечающее
.
Доказать, что
– расчетное значение зависимой
переменной, отвечающее
.
Доказать, что
 ;
; ;
; .
.
Рассмотрим парную линейную регрессионную модель
 .
По выборке объема n
= 32 получены
следующие оценки для коэффициентов
регрессии:
.
По выборке объема n
= 32 получены
следующие оценки для коэффициентов
регрессии:
 ,
,
 ,
а также стандартные ошибки этих оценок
,
а также стандартные ошибки этих оценок

 .
Найти доверительные интервалы для
коэффициентов
.
Найти доверительные интервалы для
коэффициентов
 с надежностью
с надежностью
 .
.Рассмотрим парную линейную регрессионную модель . По выборке объема
 получены следующие оценки для
коэффициентов регрессии:
получены следующие оценки для
коэффициентов регрессии:

 ,
а также стандартные ошибки этих оценок
,
а также стандартные ошибки этих оценок

 .
Найти доверительные интервалы для
коэффициентов
.
Найти доверительные интервалы для
коэффициентов
 с надежностью
с надежностью
 .
.Рассмотрим парную линейную регрессионную модель . По выборке объема
 получены следующие оценки для
коэффициентов регрессии:
получены следующие оценки для
коэффициентов регрессии:

 ,
а также стандартные ошибки этих оценок
,
а также стандартные ошибки этих оценок

 .
Являются ли полученные оценки
статистически близкими к 0 при уровне
значимости
.
Являются ли полученные оценки
статистически близкими к 0 при уровне
значимости
 ?
?Рассмотрим парную линейную регрессионную модель
 .
По выборке объема
.
По выборке объема
 получены следующие оценки для
коэффициентов регрессии:
получены следующие оценки для
коэффициентов регрессии:

 ,
а также стандартные ошибки этих оценок
,
а также стандартные ошибки этих оценок
 .
Являются ли полученные оценки
статистически близкими к 0 при уровне
значимости
?
.
Являются ли полученные оценки
статистически близкими к 0 при уровне
значимости
?Рассмотрим парную линейную регрессионную модель . По выборке объема
 получены
следующие оценки для коэффициентов
регрессии:
получены
следующие оценки для коэффициентов
регрессии:
 и
и
 ,
а также стандартные ошибки этих оценок
,
а также стандартные ошибки этих оценок
 ,
,
 .
Является ли полученная оценка
.
Является ли полученная оценка
 статистически близкой к числу 10, а
оценка
статистически близкой к числу 10, а
оценка
 статистически близкой к числу –2 при
уровне значимости
статистически близкой к числу –2 при
уровне значимости
 ?
?Рассмотрим парную линейную регрессионную модель . По выборке объема
 получены следующие оценки для
коэффициентов регрессии:
получены следующие оценки для
коэффициентов регрессии:

 ,
а также стандартные ошибки этих оценок
,
а также стандартные ошибки этих оценок
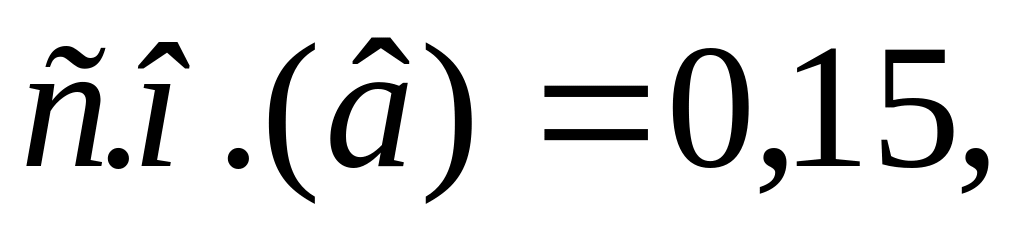
 .
Является ли полученная оценка
статистически близкой к числу – 4, а
оценка
статистически близкой к числу –1,5 при
уровне значимости
.
Является ли полученная оценка
статистически близкой к числу – 4, а
оценка
статистически близкой к числу –1,5 при
уровне значимости
 ?
?Рассмотрим парную линейную регрессионную модель . По выборке объема n = 30 получены следующие суммы квадратов:
 и
и
 .
Найти коэффициент детерминации
.
Найти коэффициент детерминации
 .
Проверить качество регрессионной
модели с помощью F-критерия
при уровне значимости
.
Проверить качество регрессионной
модели с помощью F-критерия
при уровне значимости
 .
.Рассмотрим парную линейную регрессионную модель . По выборке объема n = 23 получены коэффициент детерминации
 и величина
и величина
 .
Найти остаточную сумму квадратов
.
Найти остаточную сумму квадратов
 и регрессионную сумму квадратов
и регрессионную сумму квадратов
 .
Проверить качество регрессионной
модели с помощью F-критерия
при уровне значимости
.
Проверить качество регрессионной
модели с помощью F-критерия
при уровне значимости
 .
.Рассмотрим парную линейную регрессионную модель
 .
По выборке объема
.
По выборке объема
 получено следующее значение коэффициента
детерминации
получено следующее значение коэффициента
детерминации
 .
Проверить качество регрессионной
модели с помощью F-критерия
при уровне значимости
.
Проверить качество регрессионной
модели с помощью F-критерия
при уровне значимости
 .
.Рассмотрим парную линейную регрессионную модель . По выборке объема
 получены следующие суммы квадратов:
получены следующие суммы квадратов:
 и
и
 .
Найти коэффициент детерминации
.
Найти коэффициент детерминации
 .
Проверить качество регрессионной
модели с помощью F-критерия
при уровне значимости
.
Проверить качество регрессионной
модели с помощью F-критерия
при уровне значимости
 .
.Имеются данные о численности населения X (млн. чел.) и числе вузов Y по 7 регионам:
№ региона |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
X |
14,33 |
15,55 |
16,22 |
18,44 |
20,11 |
21,77 |
23,55 |
Y |
7 |
12 |
15 |
16 |
19 |
20 |
24 |
Постройте эмпирическое уравнение регрессии
 .
.
Вычислите стандартные ошибки коэффициентов регрессии
 и
и
 .
.Проверьте статистическую значимость эмпирических коэффициентов регрессии
 и
и
 .
.
С надежностью
 постройте доверительные интервалы для
теоретических коэффициентов регрессии
постройте доверительные интервалы для
теоретических коэффициентов регрессии
 и
и
 .
.Вычислите суммы квадратов , и
 .
Проверьте, выполняется ли равенство:
.
Вычислите коэффициент детерминации
.
.
Проверьте, выполняется ли равенство:
.
Вычислите коэффициент детерминации
.Проверьте статистическую значимость эмпирического уравнения регрессии с помощью F- критерия
 .
.
С надежностью
 постройте доверительный интервал для
среднего (ожидаемого) числа вузов,
отвечающего численности населения 19
млн. чел.
постройте доверительный интервал для
среднего (ожидаемого) числа вузов,
отвечающего численности населения 19
млн. чел.
С надежностью постройте доверительный интервал для числа вузов, отвечающего численности населения 19 млн. чел.
20. Имеются следующие данные о количестве безработных Y (%) в зависимости от уровня урбанизации (доли городского населения) X (%) для 6 экономических регионов:
№ региона |
1 |
2 |
3 |
4 |
5 |
6 |
X |
77,9 |
69,1 |
75,7 |
55,9 |
73,06 |
60,71 |
Y |
10,33 |
15,55 |
11,22 |
18,44 |
14,33 |
17,21 |
Постройте эмпирическое уравнение регрессии .
Вычислите стандартные ошибки коэффициентов регрессии
 и
.
и
.
Проверьте статистическую значимость эмпирических коэффициентов регрессии
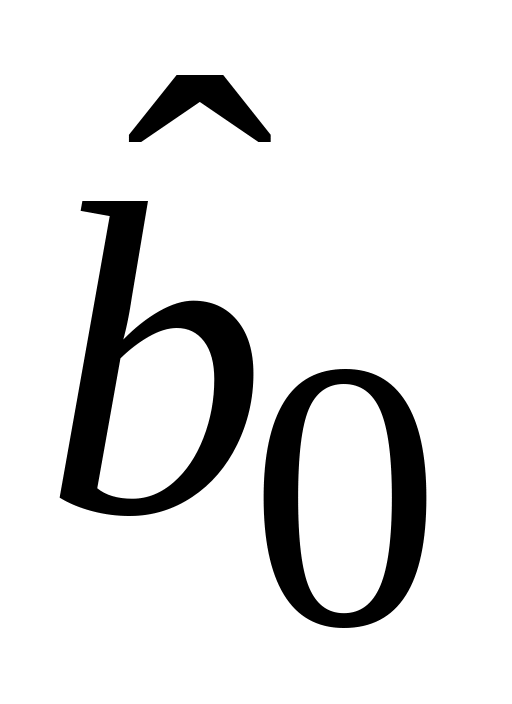 и
и
 .
.
С надежностью
 постройте доверительные интервалы для
теоретических коэффициентов регрессии
постройте доверительные интервалы для
теоретических коэффициентов регрессии
 и
.
и
.Вычислите суммы квадратов , и . Проверьте, выполняется ли равенство:
 .
Вычислите коэффициент детерминации
.
.
Вычислите коэффициент детерминации
.Проверьте статистическую значимость эмпирического уравнения регрессии с помощью F- критерия
 .
.
С надежностью
 постройте доверительный интервал для
среднего (ожидаемого) % безработных,
отвечающего 65%-ому уровню урбанизации.
постройте доверительный интервал для
среднего (ожидаемого) % безработных,
отвечающего 65%-ому уровню урбанизации.
С надежностью постройте доверительный интервал для % безработных, отвечающего 65%-ому уровню урбанизации.
