7.1.3. Теоретическая оптимизация

Теоретическая оптимизация использует методы оптимизации (рис. 15) с формализацией (МОФЦиО) или без формализации цели и ограничения.

Рис. 15. Методы оптимизации ПОС

При применении МОФЦиО детально учитываются все существующие факторы и описываются необходимые зависимости с полной реализацией общей схемы оптимизации (рис. 16). Оптимизация ПОС при помощи МОФЦиО включает два основных (укрупненных) этапа:

• создание целесообразной математической модели оптимизации;

• вычисление оптимальных значений параметров и их изменений во времени с применением этой математической модели.

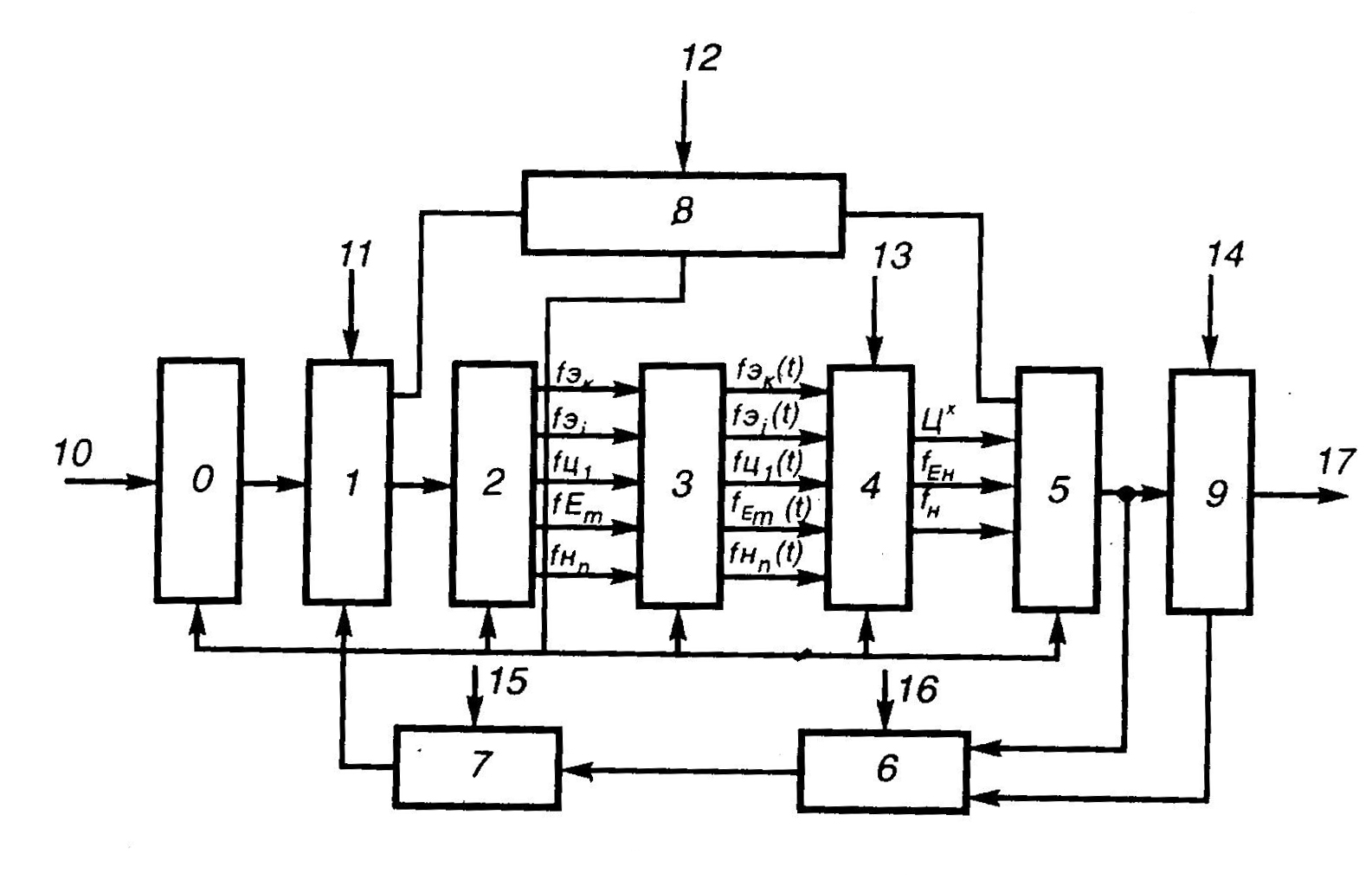
Рис. 16. Типовая структурная схема оптимизации параметров изделий:

0словесная постановка задачи для формализации; 1получение исходной и входной информации; 2составление исходных зависимостей; 3прогнозирование изменений исходных зависимостей; 4составление целевой функции и ограничений; 5разработка программ и вычисление; 6проверка постановки задач; 7коррекция; 8установление части оптимизируемых параметров непосредственным прогнозированием; 9коррекция результатов вычислений; 10задание на оптимизацию; 11,12,13,14,15,16дополнительная информация; 17оптимальные параметры.

Математическая модель оптимизации ПОС является формализованной научной абстракцией, описывающей процесс функционирования объекта в общем случае на всех этапах его существования. Таким образом, при помощи математической модели оптимизации можно рассчитывать оптимальные значения параметров данного объекта. Основой при составлении математической модели оптимизации является математическое описание различных целей создания и применения объекта, ограничений по научно-техническим, производственным и эксплуатационным возможностям (рис. 16).

Расчеты при оптимизации ПОС производятся по целевым функциям. В качестве целевой функции принимают те или иные зависимости.

Целевую функцию часто записывают в виде:

, (1)

при этом эффекты Э (определяются показателем качества) и затраты С допускается выражать в технических, денежных и условных единицах.

Для упрощения задачи иногда можно считать (например, когда фиксированы показатели качества, которые удовлетворяются), и тогда целевая функция принимает вид:

(2)

Если фиксированы затраты , то целевой функцией можно считать

(3)

Иногда целевой функцией является минимум времени выполнения некоторой работы, минимум некоторой функции потери и т.п. Целевой функцией (ЦФ) может служить и сложная функция параметров объема и времени. В качестве ЦФ иногда принимаются зависимости массы, мощности, нагрузки, вида энергии коэффициента полезного действия и другие критерии в технических единицах измерения.

В общем случае оптимизацию можно производить только по одной ЦФ, точнее при оптимизации можно максимизировать (минимизировать) только одну ЦФ. В иных случаях производят многократную оптимизацию по разным ЦФ, каждая из которых не учитывает все цели, и принимают решение после анализа полученных результатов. Также можно некоторые цели рассматривать как ограничения, без включения их в ЦФ.

При оптимизации сложных объектов трудно выбрать и формализовать одну ЦФ с единым критерием оптимальности. В таких случаях задача может быть упрощена, если удается выделить набор локальных критериев , которые являются сравнительно простыми функциями от вектора оптимизируемых параметров, а критерий F(x) – монотонная функция локальных критериев:

(4)

Критерий F(x) называют глобальным критерием. Локальными критериями могут быть частные характеристики объекта, такие, как масса, габаритные размеры, скорость, стоимость, надежность. В частных случаях задачи поиска оптимальных решений можно решать несколькими критериями на множестве F(x) , или графическим путем. Рассмотрим примеры.

Выполнение этапов оптимизации ПОС по МОФЦиО включает:

• выбор вычислительного алгоритма, составление программы для ЭВМ с реализацией выбранного алгоритма, проведение вычислений на ЭВМ по составленным программам;

• проведение анализа результатов, сопоставление их с теоретическими прогнозами и данными натурного эксперимента.

Из сопоставления выясняется, удачно ли выбрана математическая модель и вычисленный алгоритм. При необходимости они уточняются и вычисления повторяются на более совершенной основе.