В методичних вказівках подано методи переходу від неперервної задачі до дискретної шляхом заміни диференціальних рівнянь (розглянуто еліптичні, параболічні та гіперболічні) кінцево-різницевими. Розглянуто питання збіжності і стійкості чисельного розв’язку при застосуванні методу сіток. Наведено алгоритми, блок-схеми та програми (на Турбо- Паскалі ) для виконання лабораторних робіт. Для кожної з п’яти робіт складено індивідуальні завдання і наведено розв’язок контрольного прикладу.

І. Основні поняття

1.1. Класифікація диференціальних рівнянь у частинних похідних

Диференціальні рівняння в частинних похідних мають широке застосування в математичній фізиці, гідродинаміці, акустиці й інших галузях знань. Здебільшого такі рівняння в аналітичному вигляді не розв’язуються. Тому широкого розповсюдження набули методи їхнього наближеного розв’язання, зокрема, метод сіток.

Ми приділимо основну увагу питанню рішення лінійних диференціальних рівнянь другого порядку. Побудова різних схем методу сіток у випадку рівнянь у частинних похідних залежить від типу рівнянь і виду граничних умов. Зробимо кілька зауважень про класифікацію лінійних диференціальних рівнянь другого порядку.

1. Хвильове рівняння

(1.1)

До дослідження цього рівняння приводить розгляд процесів поперечних коливань струни, подовжніх коливань стрижня, електричних коливань у проводі, крутильних коливань вала, коливань газу і т.д. Це рівняння є найпростішим рівнянням гіперболічного типу.

2. Рівняння теплопровідності (дифузії)

(1.2)

До дослідження цього рівняння приводить розгляд процесів поширення тепла, дифузії рідини і газу, деякі питання теорії імовірностей і т.д. Це рівняння параболічного типу.

3.Рівняння Лапласса

(1.3)

До дослідження цього рівняння приводить розгляд задач про електричні і магнітні поля, про стаціонарний тепловий стан, задач гідродинаміки, дифузії і т.д. Це рівняння є найпростішим рівнянням еліптичного типу.

Приступимо тепер до вивчення кінцево-різницевих методів рішення рівнянь у частинних похідних. Як правило, аналітичні методи рішення рівнянь у частинних похідних зв'язані з відокремленням змінних (метод Фур'є). Використання цього методу наштовхується на великі труднощі, якщо область незалежних змінних, де знаходиться рішення, відрізняється від найпростіших (прямокутник, коло). Другою перешкодою для застосування методу Фур'є є залежність коефіцієнтів лінійного рівняння від часу і просторових змінних. Наприклад, залежність коефіцієнта а = a(t, x) у хвильовому рівнянні з функцією a(t, x) досить загального виду вже не дозволить розділити змінні.

Відзначені обмеження застосування аналітичних методів привели, особливо з розвитком обчислювальної техніки, до широкого розповсюдження чисельних методів рішення рівнянь з частинними похідними. Досвід рішення багатьох складних задач науки і техніки чисельними методами підтверджує їхню ефективність.

Рівняння (1.1), (1.2), у яких одна з незалежних перемінних t є часом, називаються нестаціонарними. Рівняння (1.3) для функції и(х, у), що залежить тільки від просторових координат х и у, є стаціонарним.

1.2. Апроксимація частинних похідних

Першим етапом у чисельному рішенні диференціальних рівнянь з частинними похідними є перехід від неперервної задачі до дискретної. Дискретизація задачі — це основа чисельного методу.

Почнемо з того, що розглянемо різниці тільки в напрямку х. Згадаємо, що розвинення в ряд Тейлора функції и(х + h, у) околі точки (х, у) можна записати у вигляді

, (1.4)

де лежить між х и x+h. З останньої рівності одержуємо

Таким чином, якщо записати за допомогою рівностей

(1,5)

то похибка апроксимації (дискретизації) буде

, (1,6)

де .

У формулі (1.5) частинна похідна виражена через праву кінцеву різницю . Виразимо через ліву різницю . Для цього в розвиненні ряду Тейлора замість (х+ h) підставимо (х - h):

, (1.7)

де При цьому одержуємо наближену рівність

(1.8)

яка виконується з похибкою, рівною:

, (1.9)

де .

У подальшому нам будуть потрібні і права (1.5) і ліва (1.8) різниці.

Тепер одержимо різницеве наближення для . Якщо и(х, у) має частинні похідні до четвертого порядку включно, тоді розвинення в ряд Тейлора функцій в околі точки (х, у) можна записати у вигляді

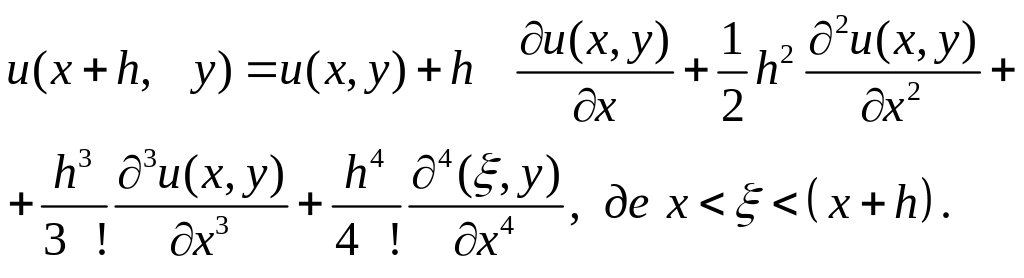
Склавши дві останні рівності одержимо рівність

,

яку позначимо (1.10) і яка виконується з точністю

, (1.11)

де

Тут розглянуто похідні в напрямку х. Такий самий аналіз можна провести для похідних у напрямку у і одержати формули, аналогічні формулам (1.4) – (1.11). Використовуючи ці вирази, можна представити диференціальні рівняння в частинних похідних (1.1) – (1.3) через кінцево-різницеві наближення (кінцево-різницеві схеми).