1.2 Содержание практических заданий
Решить следующие задачи.
Задача 1.
Время безотказной работы объекта подчиняется закону Вейбулла с параметрами В = 0,5; время работы t = 300 часов.
Определить вероятность безотказной работы P(t), частоту отказов f(t), интенсивность отказов λ(t), среднее время безотказной работы Т0.
Задача 2.
Система состоит из двух устройств. Вероятности безотказной работы каждого из них, в течение времени t = 200 часов: P1(200) = 0,75; P2(200) = 0,37.
Найти среднее время работы системы до первого отказа при экспоненциальном законе надежности.
Задача 3.
Время работы устройства до отказа подчинено экспоненциальному закону распределения с параметром λ = 1,5 · 10-5 1/ч.
Определить количественные характеристики надежности устройства: вероятность безотказной работы P(t), частоту отказов f(t), наработку на отказ, если t = 5 000 часов.
Задача 4.
Время работы изделия до отказа подчинено закону распределения Релея. Вычислить количественные характеристики надежности изделия P(t), f(t), λ(t), T0 для t = 1000 часов, если параметр распределения с = 900 часов.
Задача 5.
Среднее число отказов ремонтируемого устройства за время t′ = 300 часов – ncp = 5.
Какова вероятность того, что за время t = 50 часов работы возникнет 3; 4 отказа?
Задача 6.
Пусть время работы изделия до отказа подчинено усеченному нормальному закону с параметрами Т0 = 16 000 часов, σ = 12 000 часов. Вычислить вероятность безотказной работы изделия для t = 15 000 часов.
2 Аналитические методы расчета надежности
2.1 Краткие теоретические материалы
Под расчетом надежности понимают определение численных показателей по тем или иным числовым данным.
При аналитическом методе основные показатели надежности: вероятность безотказной работы P(t), средняя наработка на отказ Т0, определяются по известным интенсивностям отказов элементов, входящих в данную информационную систему. Элементы технической системы соединены последовательно, если отказ любого из элементов приводит к отказу всей системы.
Пусть система состоит из n последовательно соединенных элементов.
Для безотказной работы системы необходимо, чтобы каждый элемент работал безотказно. Так как отказы элементов взаимно независимы, то вероятность безотказной работы системы равна произведению вероятностей элементов.
,
(17)
где Р1, Р2, …, Рn – вероятности безотказной работы элементов; Рi – вероятность безотказной работы i-го элемента; Рс – вероятность безотказной работы системы.
Пусть функции надежности элементов подчиняются экспоненциальному закону распределения, а интенсивности отказов не зависят от времени.
где λ1, λ2,…, λn – интенсивности отказов элементов.
Тогда,
(18)
Надежность системы также подчиняется экспоненциальному закону распределения.
где λс = λ1 + λ2 + … + λn.
Среднее время безотказной работы системы Т0с = 1/λc.
Вероятность безотказной работы системы при последовательном (основном) соединении элементов всегда меньше, чем вероятность самого ненадежного элемента. Она существенно возрастает при увеличении надежности самого ненадежного элемента.
Данные по интенсивностям отказов отдельных элементов радиоэлектронных систем приведены в таблице 1.
Таблица 1 – Данные по интенсивностям отказов
Наименование элементов |
Интенсивность отказов λ·10-6, ч-1 |
Наименование элементов |
Интенсивность отказов λ·10-6, ч-1 |
Резисторы |
0,01 – 1 |
Полупроводниковые диоды |
0,12 – 50 |
Конденсаторы |
0,1 – 16 |
Полупроводниковые триоды |
0,01 – 90 |
Трансформаторы |
0,02 – 6,5 |
Коммутационные устройства |
0,003 – 3 |
Дроссели, катушки индуктивности |
0,02 – 4,4 |
Штепсельные разъемы |
0,01 – 9 |
Реле |
0,5 – 100 |
Соединения пайкой |
0,1 – 1 |
Интегральные микросхемы |
0,001 – 0,01 |
|
|
Пусть система состоит из n параллельно соединенных элементов и отказы элементов взаимно независимы. Отказ системы наступает только тогда, когда отказывают все входящие в систему элементы.
Тогда вероятность отказа системы равна произведению вероятностей отказов элементов.
(19)
где Qi(t) = 1 – Pi(t) – вероятность отказа i-го элемента в течение времени t.
Безотказная работа системы есть событие, противоположное отказу.
Вероятность безотказной работы системы
(20)
Если интенсивности отказов не зависят от времени, то формулы (19) и (20) принимают вид:
(21)
(22)
Если элементы системы имеют одинаковую надежность, т. е.
то вероятность безотказной работы системы
(23)
Средняя наработка на отказ системы
Осуществим замену переменных
Получим:
(24)
Пусть параллельно включены два элемента с неодинаковыми интенсивностями отказов.
Вероятность безотказной работы системы
Средняя наработка системы до отказа
.
При параллельном включении трех элементов с неодинаковой надежностью:
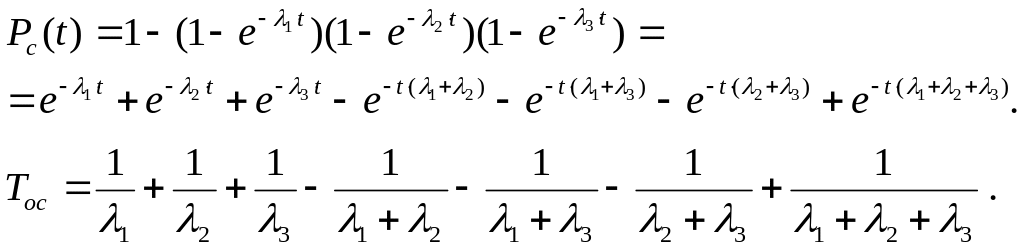
По аналогии запишем формулу для средней наработки на отказ системы с неодинаковыми элементами в общем виде:
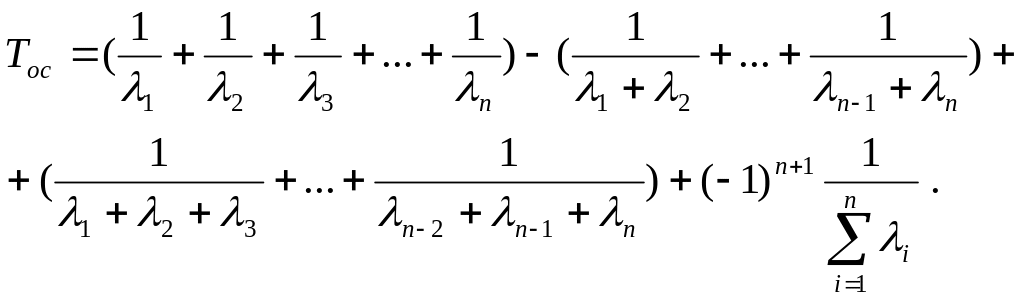(25)
При увеличении числа параллельно соединенных элементов вероятность безотказной работы системы возрастает.
Пример 7.
– вероятность
безотказной работы одного элемента.
Подключим параллельно к этому элементу другой элемент с той же надежностью. Вероятность безотказной работы двух параллельно включенных элементов
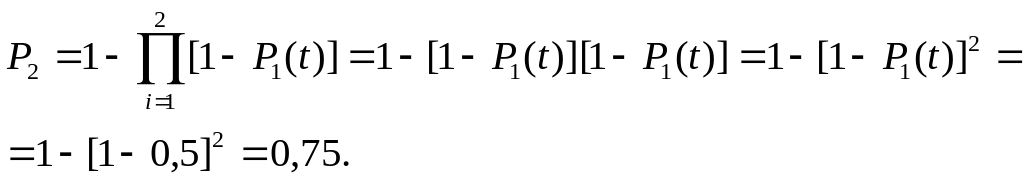
Если параллельно подключить три элемента с одинаковой надежностью, то вероятность безотказной работы системы
При четырех параллельно соединенных элементах с одинаковой надежностью
На рисунке 1 изображены системы с основным (последовательным), параллельным (резервным) и смешанным соединением элементов.
а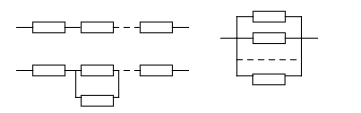
)
б)
P1(t)
P1(t) P2(t) Pn(t)
P2(t)
в)
P1(t) P2’(t) Pn(t)
Pn(t)
P2”(t)
Рисунок 1 – Системы с различными типами соединений элементов
При смешанном соединении сначала по соответствующим формулам находят надежность цепи из К последовательно соединенных элементов, затем надежность системы из m параллельных ветвей.
При определении вероятности безотказной работы системы с произвольным соединением элементов используется метод минимальных путей.
Минимальный путь – это такой минимальный набор работоспособных элементов, исключение любого из которых (т. е. отказ) переводит систему из состояния работоспособности в состояние отказа. У системы с произвольной структурой может быть несколько минимальных путей. Последовательное соединение из n элементов имеет один минимальный путь. Параллельное соединение из n элементов имеет n минимальных путей, проходящих через каждый элемент.
Пример 8.
На рисунке 2 изображена мостовая схема, где P1, P2, P3, P4, P5 – вероятности безотказной работы элементов схемы.
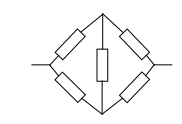Минимальные пути:
∆σς∆
1) P1, P4;
Р1 Р4 2) P1, P3, P5;
3) P2, P5;
4) P2, P3, P4.
Р3
Р2 Р5
Рисунок 2 – Мостовая схема
Схема рисунка 2 преобразуется в схему рисунка 3, состоящую из четырех параллельно включенных ветвей.
Рисунок 3 – Схема из четырех параллельно включенных ветвей
Вероятность безотказной работы системы
