Тема 2. Законы распределения и аналитические методы расчета надежности

Тема:	Законы распределения и аналитические методы расчета надежности
Учебные цели: – изучить законы распределения и аналитические методы расчета надежности; – выработать навыки работы с законами распределения и аналитическими методами расчета надежности.
Требования квалификационной характеристики: уметь использовать основные понятия и методы теории надежности технических систем.
Учебно-материальное обеспечение: компьютерный класс загруженным программным редактором MathCAD.

Прежде чем приступить к выполнению заданий, необходимо ответить на следующие вопросы:

1. Чем определяется закон распределения, используемый при оценке надежности

2. Распределение Вейбулла

3. Экспоненциальное распределение

4. Распределение Релея

5. Распределение Пуассона

6. Нормальное распределение

7. Что понимают под расчетом надежности

8. Какие показатели надежности используются при аналитическом методе расчета надежности

9. Вероятность безотказной работы системы при последовательном соединении элементов

10. Вероятность безотказной работы системы при параллельном соединении элементов в систему.

11. Вероятность безотказной работы системы при параллельном соединении двух элементов в систему

12. Вероятность безотказной работы системы при параллельном соединении трех элементов в систему

13. Схемы системы с основным (последовательным) ,параллельном (резервном) и смешанном соединении элементов в систему

1 Законы распределения, используемые при оценке надежности

1.1 Краткие теоретические или справочные материалы

Закон распределения определяется видом аналитических функций, описывающих показатели надежности: P(t), f(t), λ(t). Закон распределения случайной величины выбирается в зависимости от свойств объекта, условий его работы, характера отказов.

Согласно распределению Вейбулла, вероятность безотказной работы определяется по формуле

(1)

где λ₀ и В – параметры.

Частота отказов

(2)

Интенсивность отказов

λ = λ₀ · B · t^B-1. (3)

Среднее время безотказной работы

(4)

где – табулированная гамма-функция.

Закону Вейбулла хорошо подчиняется распределение отказов в объектах, содержащих большое количество однотипных неремонтируемых элементов (полупроводниковых приборов, микромодулей и т. д.).

Особенностью распределения Вейбулла является то, что с изменением параметра В меняется характер зависимости показателя надежности от времени. При В < 1 интенсивность отказов будет монотонно убывающей функцией, при В > 1 – возрастающей.

Данное свойство позволяет соответствующим подбором параметров λ₀ и В обеспечить хорошее совпадение результатов опытных данных с аналитическими выражениями параметров надежности.

Поведение системы на участке приработки хорошо описывается законом распределения Вейбулла с параметром В < 1, а на участке старения – В > 1.

Пример 1.

Время безотказной работы объекта подчиняется закону Вейбулла с параметрами В = 1,5; время работы t = 100 часов.

Определить вероятность безотказной работы P(t), частоту отказов f(t), интенсивность отказов λ(t), среднее время безотказной работы Т₀.

Решение.

Экспоненциальное распределение является частным случаем распределения Вейбулла при В = 1.

Интенсивность отказов λ = const.

Вероятность безотказной работы

(5)

Наработка на отказ

(6)

Экспоненциальное распределение хорошо описывает поведение системы в период нормальной эксплуатации, когда λ = const.

Это распределение не учитывает износа элементов системы.

Экспоненциальное распределение типично для большинства сложных объектов, содержащих большое количество различных неремонтируемых элементов, имеющих преимущественно внезапные отказы из-за наличия скрытых дефектов. Данное распределение применяется также к ремонтируемым объектам с простейшим потоком отказов.

Пример 2.

Система состоит из двух устройств. Вероятности безотказной работы каждого из них, в течение времени t = 100 часов: P₁(100) = 0,95; P₂(100) = 0,97.

Найти среднее время работы системы до первого отказа при экспоненциальном законе надежности.

Решение.

Вероятность безотказной работы системы

Р_с(100) = Р₁  (100) Р₂  (100) = 0,95  0,97 = 0,92,

откуда λ_с = 0,83  10^-3 1/ч.

Среднее время безотказной работы

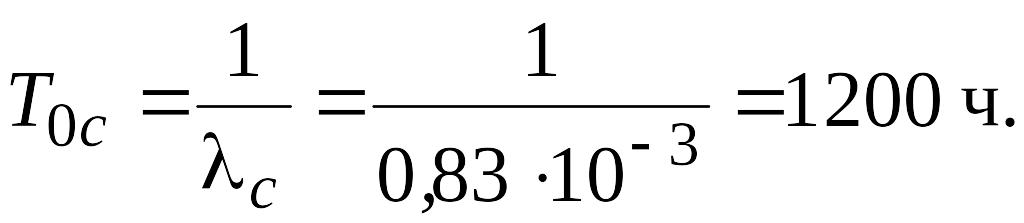
Пример 3.

Время работы устройства до отказа подчинено экспоненциальному закону распределения с параметром λ = 2,5 · 10^-5 1/ч.

Определить количественные характеристики надежности устройства: вероятность безотказной работы P(t), частоту отказов f(t), наработку на отказ, если t = 2 000 часов.

Решение.

3. Наработка на отказ, или среднее время безотказной работы,

Распределение Релея достаточно полно описывает поведение элементов и объектов с явно выраженными эффектами износа и старения.

Вероятность безотказной работы при этом распределении

(7)

где с – параметр распределения.

Частота отказов

(8)

Интенсивность отказов

. (9)

Средняя наработка на отказ

(10)

Пример 4.

Время работы изделия до отказа подчинено закону распределения Релея. Вычислить количественные характеристики надежности изделия P(t), f(t), λ(t), T₀ для t = 500 часов, если параметр распределения с = 700 часов.

Распределение Пуассона применяется для оценки надежности ремонтируемых изделий с простейшим потоком отказов.

(11)

где К – число отказов за время t; λ – интенсивность потока отказов; P_K(t) – вероятность того, что за время t произойдет К отказов.

Пример 5.

Среднее число отказов ремонтируемого устройства за время t′ = 500 часов – n_cp = 10.

Какова вероятность того, что за время t = 100 часов работы возникнет 2; 3 отказа?

.

Нормальное распределение или распределение Гаусса используется для вычисления надежности объектов, для которых типичен износ. Отказы объектов носят постепенный характер, вследствие старения элементов.

Плотность вероятности момента отказов

Она зависит от двух параметров: среднего значения времени работы до отказа Т₀ и среднеквадратичного отклонения наработки на отказ σ.

Плотность нормального распределения имеет колоколообразную форму, симметричную относительно среднего значения Т₀.

Вероятность безотказной работы

(12)

где Ф – табулированный интеграл Лапласа.

Интенсивность отказов

(13)

Нормальная плотность распределения отлична от нуля при t < 0. Этот недостаток несущественен, если Т₀ >> σ. При этом условии частью кривой распределения при t < 0 можно пренебречь. Если это условие не выполняется, то использование нормального распределения приводит к погрешностям.

Часть кривой распределения при t < 0 отсекают. Получают усеченное нормальное распределение.

Формулы к усеченному нормальному распределению следующие.

Вероятность безотказной работы:

(14)

Интенсивность отказов:

(15)

Среднее время безотказной работы:

(16)

Пример 6.

Пусть время работы изделия до отказа подчинено усеченному нормальному закону с параметрами Т₀ = 6 000 часов, σ = 2 000 часов. Вычислить вероятность безотказной работы изделия для t = 5 000 часов.

Решение.

Интенсивность отказов при нормальном и усеченном нормальном распределениях резко возрастает с течением времени, что характерно для стареющих устройств.