1.2 Содержание практических заданий

Решить следующие задачи.

Задача 1.

Одновременно испытываются 40 машин.

В течение 1000 часов непрерывной работы машин получены следующие данные.

За первый интервал работы ∆t₁ = 200 часов вышло из строя 0 машин.

За второй интервал работы ∆t₂ = 200 часов вышло из строя 1 машина.

За третий интервал работы ∆t₃ = 200 часов вышло из строя 0 машин.

За четвертый интервал работы ∆t₄ = 200 часов вышло из строя 0 машин.

За пятый интервал работы ∆t₅ = 200 часов вышла из строя 1 машина.

Определить вероятность безотказной работы машин в течение 1000 часов.

Задача 2.

На испытания поставлены N = 300 изделий. За время t = 1 000 часов отказало n = 100 изделий. За последующие ∆t = 100 часов отказало еще ∆n = 200 изделий. Определить вероятность безотказной работы в течение 1000, 1100 часов, частоту отказов, интенсивность отказов.

Задача 3.

На испытании находилось 3 000 неремонтируемых изделий. Число отказов n_i фиксировалось через каждые 300 часов работы (∆t = 300 часов). Данные об отказах сведены в таблицу.

Таблица 2 – Данные об отказах

∆ti, ч	0-300	300-600	600-900	900-1200	1200-1500	1500-1800
ni	100	80	72	25	10	36
∆ti, ч	1800-2100	2100-2400	2400-2700	2700-3000
ni	35	74	25	34

Определить вероятность безотказной работы в течение 3 000 часов и среднее время безотказной работы. Общее число отказавших элементов – 491.

2 Показатели надежности восстанавливаемых систем

2.1 Краткие теоретические материалы

Для восстанавливаемых систем характерно чередование времени исправной работы и времени восстановления (ремонтов).

Система, проработав случайное время t_p1, выходит из строя. После отказа происходит восстановление, и система работает вновь время t_p2 до отказа. Этот процесс продолжается неограниченно. Полагаем, что время восстановления пренебрежимо мало по сравнению со временем работы. Можно считать, что восстановление происходит мгновенно. Отказавший, испорченный элемент немедленно заменяется новым. Элемент после восстановления имеет такую же надежность, что и в начальный момент.

Пусть интервалы времени безотказной работы между двумя соседними отказами распределены по экспоненциальному закону. Тогда вероятность того, что за промежуток времени t в системе произойдет n отказов, определится по формуле Пуассона:

, (n = 0, 1, 2, 3, …),

где λ – среднее число отказов в единицу времени или интенсивность отказов, λ = const;

λ = Λ, где Λ – параметр потока отказов. Этот параметр определяется по статистической формуле:

, (12)

где N – общее число отказавших элементов, или число восстановлений, остается неизменным. Отказавшие элементы заменяются новыми.

Поток отказов восстанавливаемой системы является простейшим, пуассоновским.

Для ремонтируемых объектов удобным для практики критерием надежности является среднее время работы между двумя соседними отказами или наработка на отказ Т₀.

Значения этого параметра определяются по результатам обработки статистического материала, полученного в ходе эксплуатации или экспериментов.

Если устройство проработало суммарное время t_∑ и имело при этом n отказов в работе, то наработка на отказ

. (13)

Если испытывались N однотипных объектов, то необходимо просуммировать время исправной работы по всем объектам и разделить его на общее число отказов:

. (14)

Для простейшего потока параметр потока отказов определяются по формуле:

. (15)

Пример 4.

Наблюдалась работа трех экземпляров однотипной аппаратуры. За период наблюдений зафиксировано по первому экземпляру аппаратуры 6 отказов, по второму – 10, по третьему – 7.

Наработка первого экземпляра – 4 800 часов, второго – 6 260 часов, третьего – 5 500 часов.

Определить среднее время работы аппаратуры .

Решение.

1. Суммарное время работы трех образцов аппаратуры

t_∑ = 4 800 + 6 260 + 5500 = 16 560 часов.

2. Суммарное количество отказов

n = 6 + 10 + 7 = 23.

3. Средняя наработка на отказ, или среднее время работы между отказами,

Пример 5.

Приемник к началу наблюдений за отказами проработал 470 часов. К концу наблюдений время работы составило 18 500 часов. Зарегистрировано 15 отказов.

Определить среднюю наработку на отказ.

Решение.

1. Суммарное время работы приемника

t_∑ = 18500 – 470 = 18 030 ч.

2. Средняя наработка на отказ

Пример 6.

В результате эксплуатации N = 100 ремонтируемых объектов получены следующие статистические данные об отказах

Таблица 3 – Статистические данные об отказах

ni	46	40	36	32	30	28	26	24
∆t · 103, ч	2	2	2	2	2	2	2	2

n_i – число отказов в интервале времени ∆t.

Найти параметр потока отказов и среднюю наработку на отказ

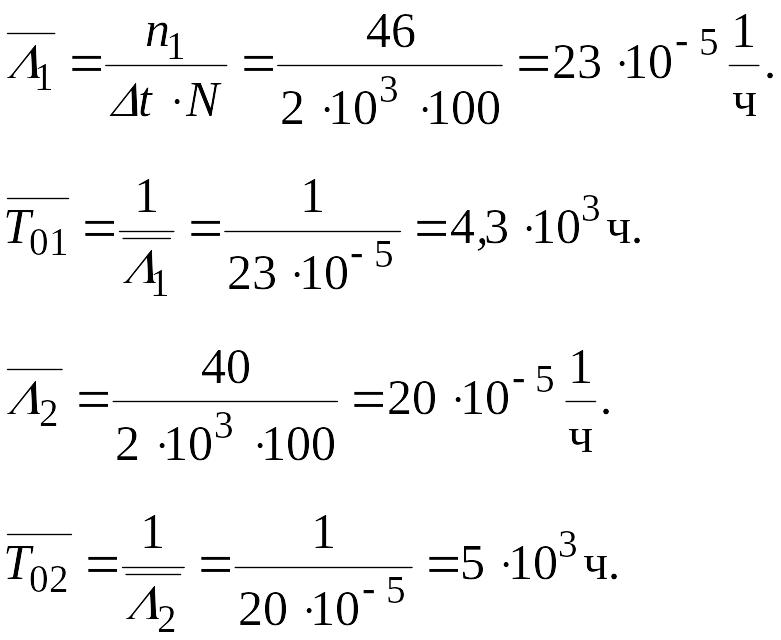
Восстановление отказавшего элемента часто требует времени, которым нельзя пренебречь. Среднее время восстановления системы Т_в – это математическое ожидание продолжительности восстановления системы после отказа, т. е. среднее время вынужденного, нерегламентированного простоя, вызванного отысканием и устранением отказа.

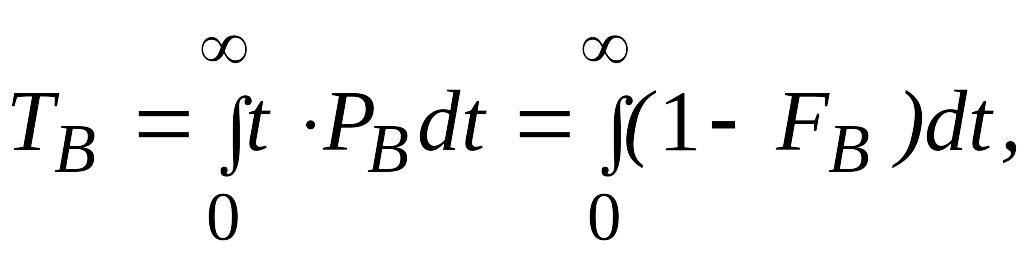(16)

где Р_в – плотность вероятности времени восстановления; F_в – функция распределения времени восстановления.

Основной характеристикой восстанавливаемой системы является коэффициент готовности. Коэффициент готовности К_г для установившегося режима эксплуатации определяется как вероятность того, что система будет исправна в произвольно выбранный момент в промежутках между плановыми техническими обслуживаниями

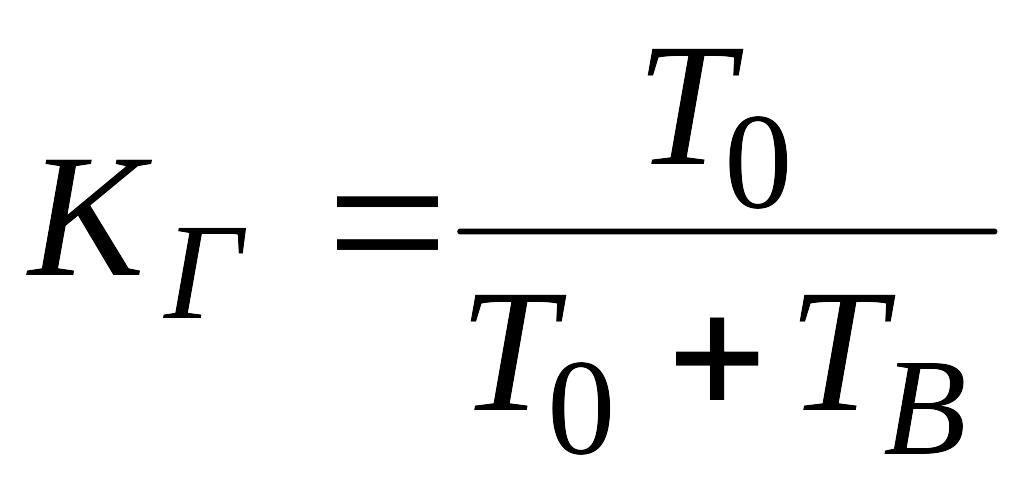. (17)

Формулы для статистических оценок времени восстановления и коэффициента готовности имеют вид:

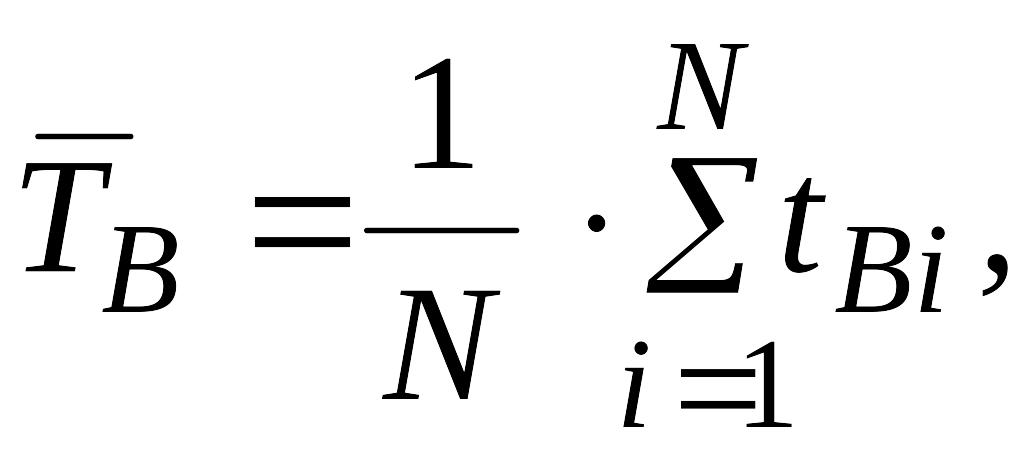(18)

, (19)

где N – число восстановлений системы;

t_Вi – время восстановления (ремонта) системы после i-го отказа.

Пример 7.

В результате испытаний 35 ремонтируемых объектов в течение t = 1 000 часов была получена интенсивность отказов . Закон распределения отказов – экспоненциальный. Время ремонта является случайной величиной, принимающей значение t_В1 = 3 часа с вероятностью Р₁ = 0,6, значение t_В2 = 3,2 часа с вероятностью Р₂ = 0,2 и значение t_В3 = 3,5 часа с вероятностью Р₃ = 0,2.

Найти вероятность безотказной работы в течение 1 000 часов, среднее время работы между соседними отказами , среднее время восстановления , коэффициент готовности .

Решение.

1. .

2.

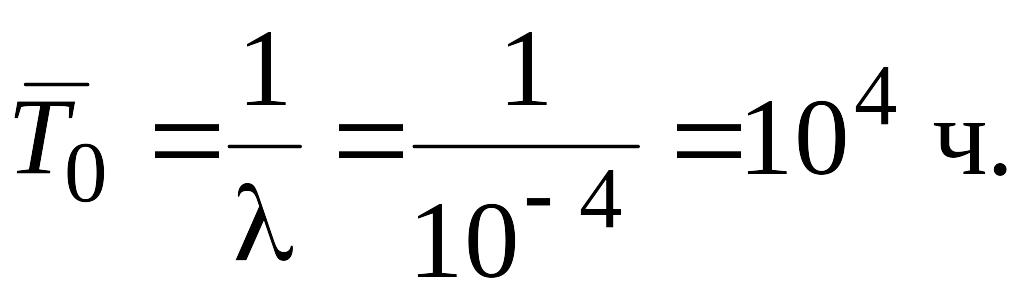
3.

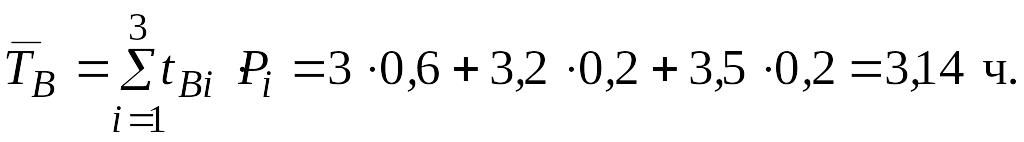
4.

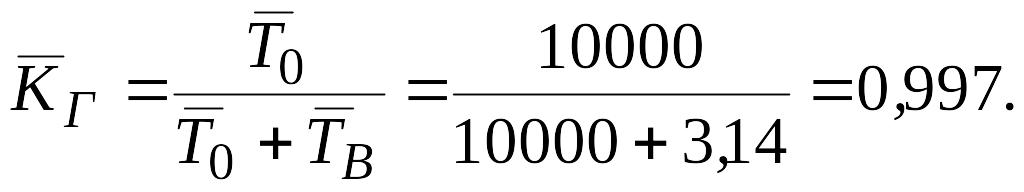
Пример 8.

Приемник к началу наблюдения за отказами проработал 458 часов. К концу наблюдения наработка составила 2 783 часа. Всего зарегистрировано 5 отказов. Среднее время ремонта составило 1,5 часа.

Определить среднюю наработку на отказ и коэффициент готовности .

Решение.

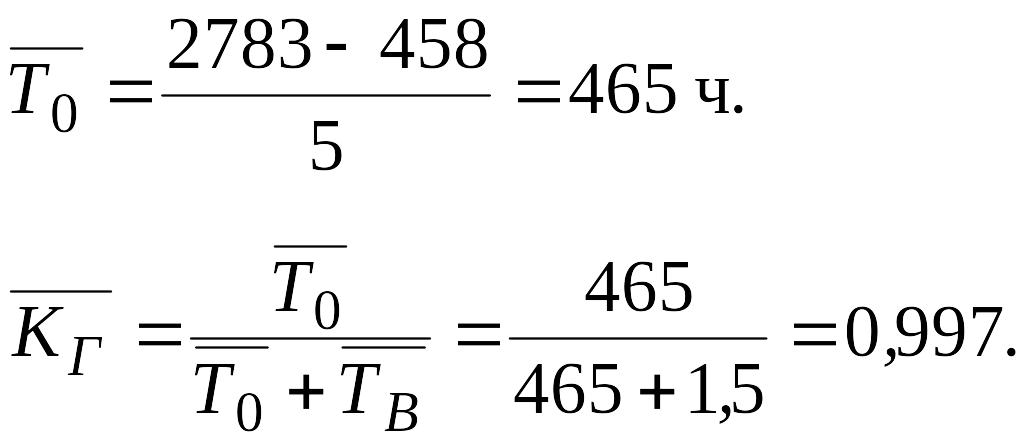
Коэффициент технического использования – это отношение времени пребывания объекта в работоспособном состоянии к сумме времени пребывания в работоспособном состоянии, времени простоев, обусловленных техническим обслуживанием, и времени ремонтов.

,

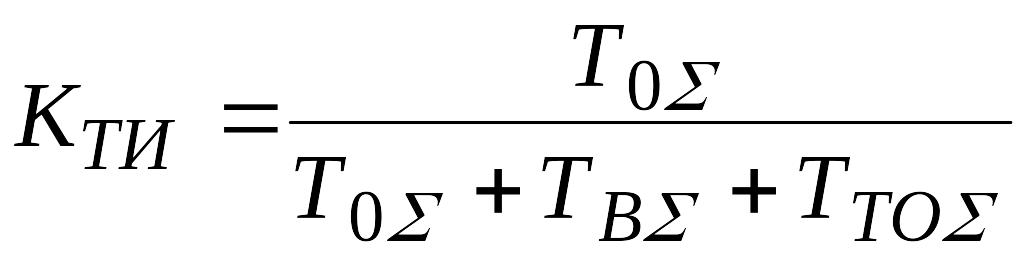где Т_0∑ – суммарная наработка;

Т_В∑ – суммарное время простоев из-за ремонтов;

Т_ТО∑ – суммарное время простоев из-за техобслуживания.

Пример 9.

При эксплуатации объекта в течение года его суммарная наработка составила Т_0∑ = 7 400 часов, суммарное время ремонтов – Т_В∑ = 480 часов, суммарное время технического обслуживания – Т_ТО∑ = 880 часов.

Определить коэффициент технического использования К_ТИ.

Решение.

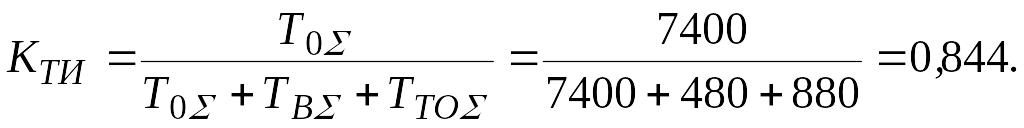
Пример 10.

Имеется 5 комплектов однотипной аппаратуры, работающих в одинаковых условиях. Число отказов, промежутки времени исправной работы между соседними отказами, время восстановления по каждому комплекту приведены в таблице.

Определить среднюю наработку на отказ и коэффициент готовности одного комплекта, таблица 3.

Таблица 4 – Комплекты и количество отказов

Номер комплекта	ti, ч										Количествоотказов	Твсрч
	tp1	tB1	tp2	tB2	tp3	tB3	tp4	tB4	tp5	tB5
1	29	0,9	46	0,7	54	0,8	25	1	34	1,2	6	0,92
2	48	0,96	60	0,8	56	1,4	36	1,15	-	-	4	1,08
3	68	1,2	64	0,95	52	1,3	-	-	-	-	3	1,15
4	34	1,3	51	0,78	56	1,25	42	1,35	-	-	5	1,17
5	52	1,25	26	1,35	38	0,98	48	1,18	-	-	4	1,19

Решение.

1. Общее время исправной работы

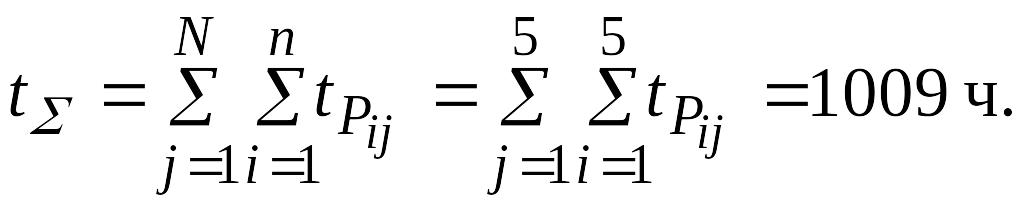
2. Общее число отказов

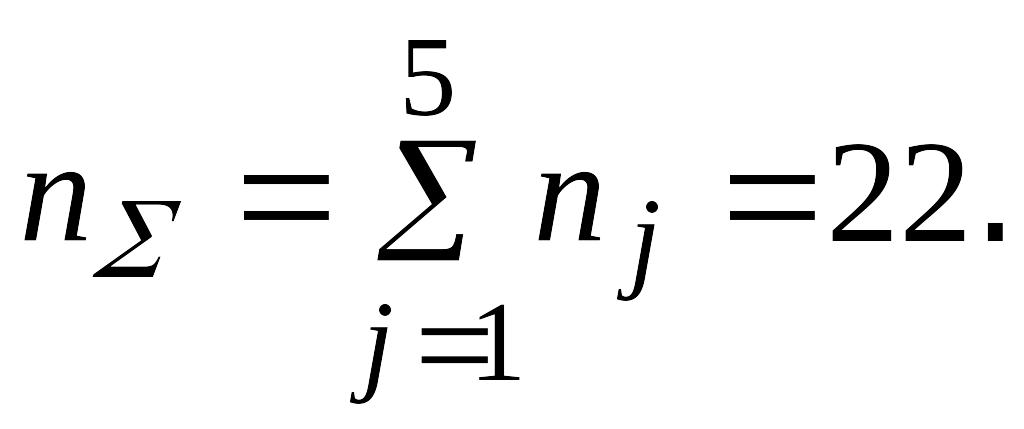
3. Средняя продолжительность ремонта

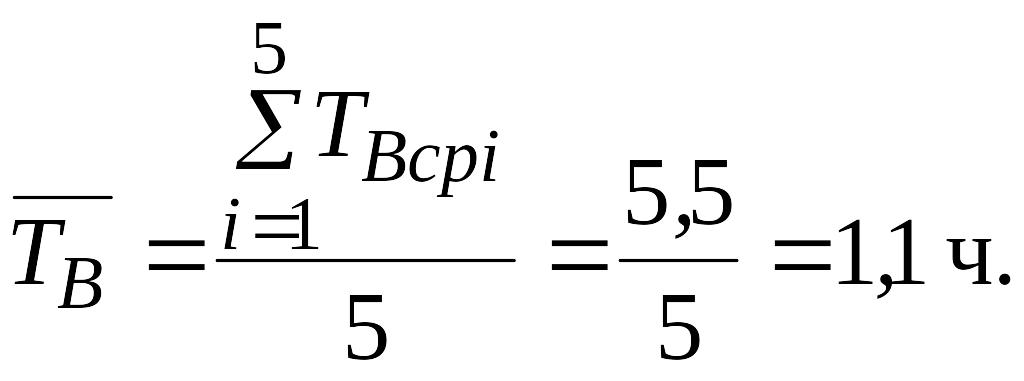
4. Средняя наработка на отказ

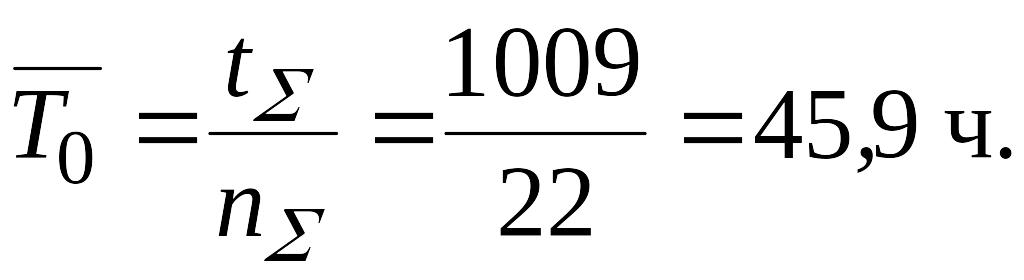
5. Коэффициент готовности