10. Ожидаемые значения риска

Ожидаемые значения (expected values) являются способом объединения вероятности и последствий риска в понятном виде. Расчет ожидаемого значения риска является простым умножением вероятности на число, соответствующе последствиям. Так как результат является в большей степени количественным, чем обычные субъектив­ные значения вероятности и последствий, то правильнее будет складывать ожидаемые значения, чтобы получить суммарный риск проекта.

С помощью ожидаемых значений мы можем осуществить оценку благоприятных воз­можностей и рисков, связанных с проектом. Ожидаемое значение также дает хорошую ориен­тацию в отношении количества денег, которые могут быть затрачены на исключение риска.

Допустим, что есть вероятность 10% возникновения риска, который бы имел послед­ствия для проекта, равные $10 000. Ожидаемое значение этого риска будет равно $1000. Если можно полностью избежать этого риска, потратив $900, то такое решение считалось бы хорошим.

Другой способ взглянуть на ожидаемое значение - это представить проект выпол­няющимся многие сотни раз. При вероятности риска 10%, он, вероятно, возникнет в 10% проектов. Средняя стоимость его для всех проектов будет равна 10% последствий суммарного риска.

Также интересно посмотреть на наилучшую и наихудшую ситуации для проекта. Это простой аналитический метод, позволяющий понять крайние возможные исходы, которые могут получиться. Он полезен при рассмотрении толерантности к риску отдельных лиц или групп. При вычислении ожидаемого значения для наилучшей ситуации предполагается воз­никновение всех положительных рисков без учета отрицательных. При вычислении ожидаемого значения для наихудшей ситуации считается, что возникнут все отрицательные риски.

Матожидание = сумма вероятностей*результат.

Дисперсия = среднее арифметическое от суммы квадратов отклонений величин xi от их среднего арифметического.

Событие риска	Последствия	Вероятность	Ожидаемое значение
Стоимость проекта	-2,000,000		-2,000,000
Доход от проекта	2,200,000		+2,200,000
Непрохождение приемочного теста	-100,000	10%	-10,000
Невыполнение гарантийных обязательств	-40,000	15%	-6,000
Дополнительные заказы	75,000	30%	+22,500
Штрафы за позднее выполнение	-50,000	5%	-2,500
Вознаграждение за раннее выполнение	100,000	30%	+30,000
Ожидаемый итог проекта (сумма всех ожидаемых значений)			234,000
Наилучшая ситуация (все хорошие риски происходят, и не происходит ни одного плохого риска)			375,000
Наихудшая ситуация (все плохие риски происходят, и не происходит ни одного хорошего риска)			10,000

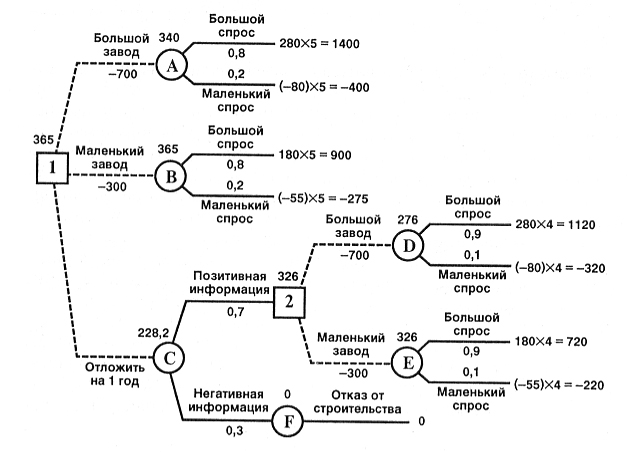
В более сложных ситуациях используется метод, называемый анализом дерева решений.