4. Інтервали можливих змін запасів дефіцитних ресурсів, в межах яких двоїсті оцінки уі залишаються на рівні оптимальних значень

а) Зміна запасу 1-го ресурсу: _ΔА: А´=А+_ΔА

Х ⁰ = ( )

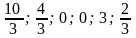Х ⁰ = (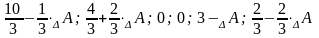 ) – всі значення є невід’ємними

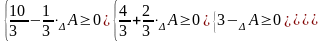
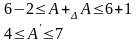
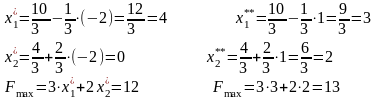
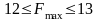(тис. $)

б) Зміна запасу 2-го ресурсу: В′ = В + _ΔВ

“Старе” Х ⁰ = ( )

“Нове” Х ⁰ = ( ) – значення х _і⁰ – невід’ємні

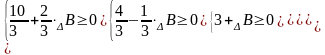
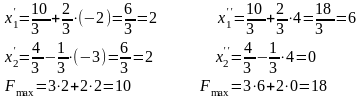
(тис. $)

Тема*: Зведення задачі длп до задачі лінійного програмування

Підприємство виготовляє продукцію 3-х видів А, В, С, для чого використовує три види ресурсів І. ІІ, ІІІ. Норми витрат ресурсів на одиницю продукції, запаси ресурсів на підприємстві, ціну і собівартість кожного виду продукції наведено в таблиці:

Вид ресурсу	Норми витрат на одиницю продукції за видами			Запас ресурсу
	А	В	С
І ІІ ІІІ	1 2 1	2 4 1	4 2 2	360 520 220
Ціна продукції	90	110	150
Собівартість	50	60	84

Розрахувати оптимальний план виробництва продукції кожного виду з використанням ресурсів, щоб рентабельність виробництва продукції була максимальною.

• Математична модель задачі:

Цільова функція – функція рентабельності виробництва продукції

max Z =

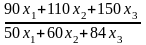
Система обмежень 1·x₁ + 2 x₂ +4 x₃ ≤ 360,

2·x₁ + 4 x₂ +2 x₃ ≤ 520,

1·x₁ + 2 x₂ +2 x₃ ≤ 220, x_j ≥ 0

• Позначимо 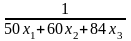= y₀ і введемо заміну змінних y_j= y_{0 ·}x_j (j=1_,2,3).

• Тоді ЦФ матиме вигляд: Z = 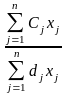= 90 y₁ + 110 y₂ + 150 y_3.

Отримали ЦФ, що виражена лінійною залежністю.

• Оскільки y_j = y_{0 ·} x_j ( j=1_,2,3 ), то х_j = .

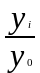Підставимо виражені через нові змінні значення х_j до системи обмежень :

1·y₁ + 2 y₂ +4 y₃ ≤ 360 y₀ ,

2·y₁ + 4 y₂ +2 y₃ ≤ 520 y₀ ,

1·y₁ + 2 y₂ +2 y₃ ≤ 220 y₀ , y_1, y_2, y₃ ≥ 0.

1·y₁ + 2 y₂ +4 y₃ - 360 y₀ ≤ 0 ,

2·y₁ + 4 y₂ +2 y₃ - 520 y₀ ≤ 0,

1·y₁ + 2 y₂ +2 y₃ - 220 y₀ ≤ 0 , y_1, y_2, y₃ ≥ 0.

• Долучаємо до системи обмежень додаткову умову – введені підстановки

= y₀ =

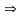
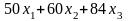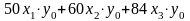= 1

50·y₁ + 60·y₁ + 84·y₁ =1

За умовою невідємності змінних y_j 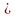0 ( j=1,2,3_,), y₀ 0.

• Виконані перетворення приводять до такої моделі задачі:

Z max = 90 y₁ + 110 y₂ + 150 y_3.

1·y₁ + 2 y₂ +4 y₃ - 360 y₀ ≤ 0 ,

2·y₁ + 4 y₂ +2 y₃ - 520 y₀ ≤ 0,

1·y₁ + 2 y₂ +2 y₃ - 220 y₀ ≤ 0,

50·y₁ + 60·y₁ + 84·y₁ =1.

y_1, y_{2 ,}y₃ ≥ 0, y₀ >0.

Отримали задачу ЛП, розвязками якої будуть Y^* = ( y₀^*; y₁^*; y₂^* ;…; y_n^*)

• Оптимальне значення початкової задачі визначають за формулою:

х_j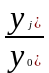^*= (j=1_,2,3)