4 Головна та побічна діагоналі

Матриці, у яких число рядків дорівнює числу стовпців, називаються квадратними, у таких матриць є головна й побічна діагоналі. Ці поняття широко використовуються при обробці матриць.

Головна діагональ – це елементи, розташовані на діагоналі, що проходить із лівого верхнього кута в нижній правий кут матриці.

Рисунок 1 – Головна діагональ матриці

В елементах матриці, що належать головній діагоналі, номер рядка і збігається з номером стовпця j. Таким чином, умовою знаходження елемента матриці на її головній діагоналі є виконання рівності i=j. При i>j елементи знаходяться під, а при i<j – над головною діагоналлю.

До побічної діагоналі квадратної матриці належать елементи, розташовані на діагоналі, що проходить із її верхнього правого кута в лівий нижній кут.

Рисунок 2 – Побічна діагональ

Припустимо, що число стовпців і число рядків матриці дорівнює n. Тоді для елементів матриці, розташованих на її побічній діагоналі, справедливі наступні рівності:

i=1, j=n;

i=2, j=n-1;

i=3, j=n-2;

…

i=n, j=1.

Аналіз цих рівностей дозволяє одержати співвідношення, що зв'язує номери рядка й стовпця елемента побічної діагоналі: 1=n-j+1.

При i>n-j+1 елементи лежать під, а при i<n-j+1 – над побічною діагоналлю.

6 Ввід матриці

Матриця – це таблиця чисел, розташованих на перетині заданого числа рядків і стовпців. Тому зручніше за всі її елементи вводити в пам’ять комп'ютера (і виводити на екран) елемент за елементом кожного рядка.

При такому введенні даних кожний елемент рядка повинен відділятися від сусіднього одним або більшим числом пробілів, а наприкінці кожного рядка (у тому числі й останнього), коли набрані всі її елементи, варто натиснути клавішу Enter. Остання операція переносить набрані значення поточного рядка в оперативну пам'ять комп'ютера й переводить курсор у початок наступного рядка.

Нижче наведений фрагмент програми, яка реалізує ввід матриці М, що складається з n_st рядків і n_cl стовпців (колонок):

for i:=1 to n_st do

for j:=1 to n_cl do

read(M[i,j]); {зчитування елемента матриці}

Якщо уважно вводити дані, тобто щоб в результаті в кожному рядку виявилося б не більше n_st елементів, то введення всіх елементів матриці було б правильним. Однак, якщо в якому-небудь рядку після n_cl елемента помилково ввести одне або більше чисел, то вони будуть введені як відповідні елементи наступного рядка, відбудеться зсув всіх наступних елементів, і в підсумку матриця буде введена неправильно.

Для зменшення впливу таких помилок необхідно, щоб програма після введення n_cl елемента кожного рядка переводила покажчик екрана на початок наступного рядка. Це можливо здійснити оператором readln.

for i:=1 to n_st do

begin

for j:=1 to n_cl do

read(M[i,j]); {зчитування елемента матриці}

readln; {встановлення вказівника на початок нового рядка після зчитування елемента в стовпці з номером n_cl}

end; {for_i}

7 Виведення матриці

Для виведення елементів матриці у вигляді рядків і стовпців рекомендується застосовувати наступний блок програми:

for i:=1 to n_st do

begin

for j:=1 to n_cl do

write(M[i,j]:4); {виведення елемента матриці}

writeln; {встановлення вказівника на початок наступного рядка після виведення елемента в стовпці з номером n_cl}

end; {for_i}

Цей фрагмент здійснює виведення матриці за рядками: спочатку виводиться перший рядок, під ним виводиться другий й так далі. Можна, звичайно, здійснити виведення матриці й за стовпцями. Однак у цьому випадку відповідна частина програми буде більше складною:

for j:=n_cl downto 1 do

begin

for i:=1 to n_st do

begin

writeln(M[i,j]:4*j);

GoToXY(WhereX-j*4, WhereY+1);

end; {for_i}

GoToXY(WhereX, WhereY-n_st);

end; {for_j}

GoToXY(whereX, WhereY+n_st);

У цьому фрагменті функції WhereX, WhereY визначають координати поточного положення курсору, а процедура GoToXY встановлює курсор у позицію із заданими координатами.

Приклад 1:

Задано двовимірний масив (матриця) розмірності m×n, елементами якої є цілі числа. Виконати «дзеркальне відображення» елементів матриці відносно вертикальної осі симетрії (поміняти місцями елементи першого стовпця з останнім, другого з передостаннім тощо).

program VertMirrow;

uses Crt;

const m=10; {число рядків}

n=15; {число стовпців}

type

TMatr=array[1..m,1..n] of integer;

var

Matr: TMatr; {вихідна матриця}

B:integer;

i,j: integer;

beign

clrscr;

writeln('Введіть поелементно матрицю');

for i:=1 to m do

begin

for j:=1 to n do

read(Matr[i,j]); {зчитування елемента матриці}

readln; {встановлення вказівника на початок нового рядка після зчитування елемента в стовпці з номером n}

end; {for_i}

{“Дзеркальне” відображення матриці відносно вертикальної осі симетрії}

for j:=1 to n div 2 do {беремо стовпці від 1-го до середнього}

for i:=1 to m do {міняємо місцями симетричні стовпці}

begin

B:=Matr[i,j];

Matr[i,j]:=Matr[i,n-j+1];

Matr[i,n-j+1]:=B;

end;

writeln('Перетворена матриця');

for i:=1 to m do

begin

for j:=1 to n do

write(Matr[i,j]:4); {виведення елемента матриці}

writeln; {встановлення вказівника на початок наступного рядка після виведення елемента в стовпці з номером n}

end; {for_i}

end.

Приклад 2:

Задана квадратна матриця порядку n, елементами якої є цілі числа. Вивести значення елементів на друк, зробивши обхід за «спіраллю», як показано на рисунку:

Розглянемо схему, яка відображає закономірності змінення індексів для виконання обходу за «спіраллю».

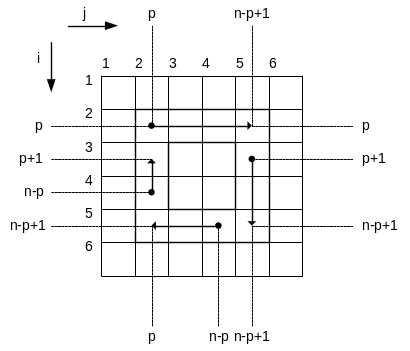
Програма, що відповідає наведеній схемі буде мати наступний вигляд:

program VertMirrow;

uses Crt;

const n=10; {порядок квадратної матриці}

type

TMatr=array[1..n,1..n] of integer;

var

Matr: TMatr; {вихідна матриця}

p:integer;

i,j: integer;

beign

clrscr;

writeln('Введіть поелементно матрицю');

for i:=1 to n do

begin

for j:=1 to n do

read(Matr[i,j]); {зчитування елемента матриці}

readln; {встановлення вказівника на початок нового рядка після зчитування елемента в стовпці з номером n}

end; {for_i}

{запис елементів матриці за “спіраллю”}

for p:=1 to (n+1) div 2 do

begin

{запис елементів верхнього рядка р-го “витка”}

for j:=p to n-p+1 do write(Matr[p,j]:4);

{запис елементів правого стовпця р-го “витка”}

for i:=p+1 to n-p+1 do write(Matr[i,n-p+1]:4);

{запис елементів нижнього рядка р-го “витка”}

for j:=n-p downto p do write(Matr[n-p+1,j]:4);

{запис елементів лівого стовпця р-го “витка”}

for i:=n-p downto p+1 do write(Matr[i,p]:4);

end;

writeln('Перетворена матриця');

for i:=1 to n do

begin

for j:=1 to n do

write(Matr[i,j]:4); {виведення елемента матриці}

writeln; {встановлення вказівника на початок наступного рядка після виведення елемента в стовпці з номером n}

end; {for_i}

end.