Из треугольника авр:

Х_Р =Х_А + cos (АР); У_Р = У_А + sin (АР).

Из треугольника ВСР: (.13)

Х_Р =Х_С + cos (СР); У_Р = У_С + sin (СР).

При решении прямой засечки по таблицам логарифмов формулы (9), (12) и (13) логарифмируются.

При вычислении прямой засечки по измеренным углам по таблицам логарифмов промежуточный контроль осуществляется путем сравнения логарифмов стороны , полученных при решении треугольников АВР и ВСР. Если засечка выполнялась с помощью теодолита, то значения логарифмов стороны не должны различаться более чем на 60 единиц пятизначного логарифма или не более чем на 100 единиц при засечке с помощью буссоли.

Прямая засечка считается выполненной правильно, если расхождения в координатах точки Р, полученных с пунктов А и С, не превышают 20 м при измерении углов теодолитов (КТД-1) и 25 м при измерении углов буссолью. За окончательное значение координат принимают их среднее значение с округлением до целых метров.

Для вычисления прямой засечки по измеренным углам на ЭКВМ выведем рабочие формулы определения координат вершины Р из одного треугольника. Очевидно, что из второго треугольника координаты точки Р будут получены по тем же формулам с заменой соответствующих обозначений.

Формулы имеют вид:

Х_Р =Х_А + cos (АР); У_Р = У_А + sin (АР),

но (АР) = (АВ) – α, следовательно,

Х_Р =Х_А + [ cos (АВ) cos α +sin (АВ) sin α];

У_Р = У_А + [ sin (АВ) cos α – cos (АВ) sin α].

Зная, что

; ,

после подстановки получим:

Х_Р =Х_А + [ (Х_В – Х_А) cos α +(У_А-У_В) sin α];

У_Р = У_А + [ (У_А-У_В) cos α – (Х_В – Х_А) sin α]. (14)

Из треугольника АВР по теореме синусов определим

,

но γ = 180⁰ – (α + β), поэтому

,

.

После подстановки формулы (3.14) примут вид:

,

.

Вынесем в числителе за скобки sin α и разделим числитель и знаменатель на sin α sin β.

Получим: ;

.

После преобразований получим в окончательном виде рабочие формулы:

;

. (15)

При вычислении прямой засечки расхождение в длине стороны ВР не должно превышать:

- по измеренным углам на ЭКВМ - 3 м;

- при вычислении с помощью счислителя СТМ - 10 м.

Форма бланка для решения задач с помощью ЭКВМ может изме­няться в зависимости от возможности машины и подготовки вычисли­теля. Даже в этой форме графа котангенсов необязательна.

Пример 5

Позиция радиолокационной станции привязывается прямой засеч­кой по измеренным углам от пункта ГГС "Широкое", сигн. и пунктов СГС N 4, пир. и N 5, пир. Абрис привязки на рис. 14. Углы измеряются теодолитом ТТ-3. Вычисления выполняются с помощью ЭКВМ на бланке (табл.2).

ЭКВМ дает возможность решить задачу только с одной промежуточной записью - числителя. Имея перед собой программу последовательности нажатия клавиш и исходные данные, можно вообще не пользоваться вычислительным бланком.

Рис. 14. Абрис для прямой засечки

Таблица 2

Решение прямой засечки с помощью ЭКВМ

Название (номер) точки (пункта)	Угол	Абсциссы хА хВ хР	ctga ctgb ctga + ctgb	Ординаты yА yВ yР
Широкое В N 4, пир. Р АРСОМ В N 4, пир. С N 5, пир. Р АРСОМ	78 36,8 66 13,1 46 21,2 95 37,0	25 624,5 27 822,7 28 328,6 27 822,7 29 970,0 28 234,0	0,20139 0,44067 0,64206 0,95384 0,09834 1,05218	18 268,7 19 562,2 15 250,8 19 562,2 17 946,8 16 056,9
хРср = 28281,3 yРср = 15653,9

Разновидностью прямой засечки по измеренным углам является случай, когда между пунктами А, В и С отсутствует видимость (рис. 15, а).

а

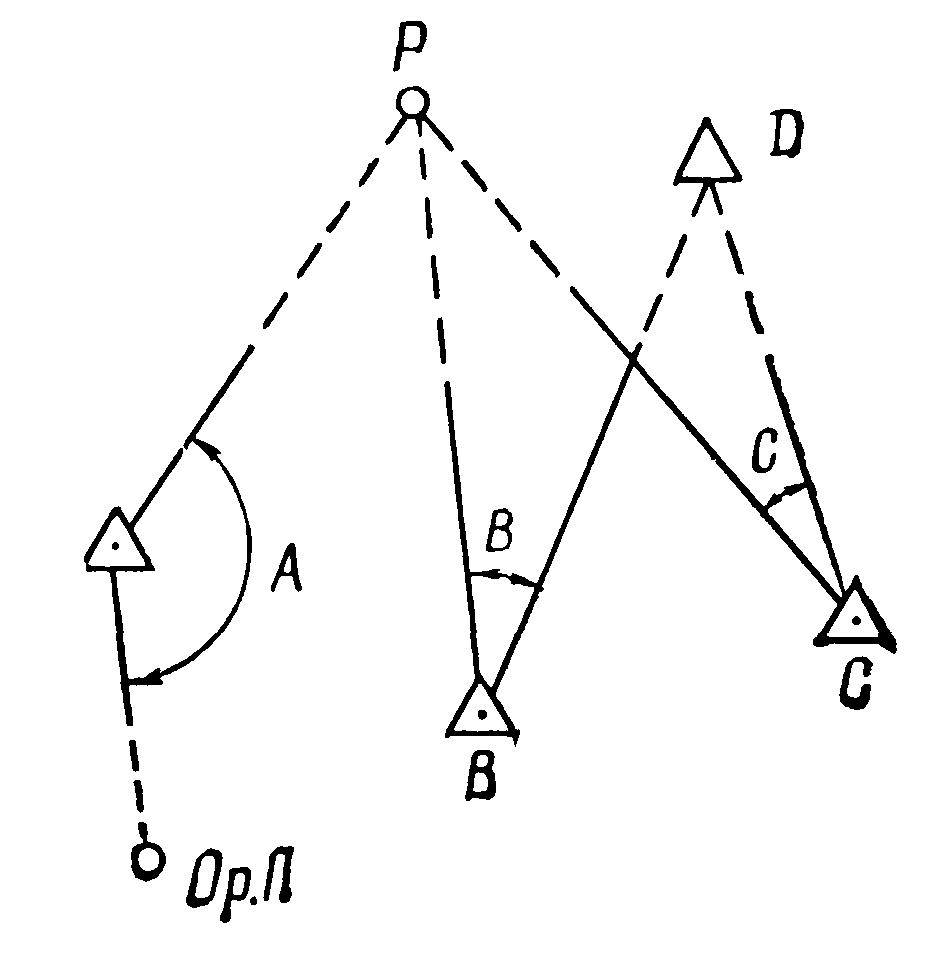
б

Рис. 15. Разновидность прямой засечки по измеренным углам:

а - от общего ориентира ; б- от разных ориентиров

Но с каждого из этих пунктов наблюдается четвертый пункт D и дирекционные углы (АD), (BD) и (CD) известны или могут быть вычислены решением ОГЗ и по измеренным А, В и С можно получить дирекционные углы направлений с исходных пунктов на определяемую точку (АР), (ВР) и (СР).

В этом случае засечка вычисляется в следующем порядке:

1. Решением обратных геодезических задач по координатам пунктов А, В, С и D вычисляют дирекционные углы (АВ), (ВС), (АD), (BD) и (CD).

2. По дирекционным углам (АD), (BD) и (CD) и измеренным углам на пунктах А, В и С находят дирекционные углы направлений АР, ВР и СР.

На рис. 10, а изображены два случая положения пункта D относительно направлений АР, ВР и СР.

В первом случае: (АР) = (АD) + А;

(ВР) = (ВD) + В; (16)

(СР) = (СD) + С.

Во втором случае:

(АР) = (АD) + А;

(ВР) = (ВD) + В; (17)

(СР) = (СD) + С.

В общем случае, если измеренный угол будет правым относительно направления на пункт D, он вычитается, если левым, - складывается.

3. По разности дирекционных углов сторон треугольников АВР и ВСР определяют внутренние углы α₁, β₁, и α₂, β₂ :

α₁ = (АВ) – (АР); α₂ = (ВС) – (ВР) ;

β₁ = (ВР) – (АВ) ± 180⁰; β₂ = (СР) – (ВС) ± 180⁰. (18)

Дальнейшие вычисления выполняются так же, как и при прямой засечке при наличии видимости между исходными пунктами.

Если отсутствует общий ориентир (пункт D), но с каждого из исходных пунктов А, В и С наблюдаются пункты с известными координатами или ориентирные пункты (рис.15,б), дирекционные углы направлений на которые могут быть получены из каталогов, прямая засечка решается в том же порядке.

Прямой засечкой ориентированным прибором называется способ определения координат привязываемой точки Р (рис.16) по дирекционным углам направлений на нее (АР), (ВР) и (СР) с трех исходных пунктов А, В и С.

На каждом исходном пункте прибор ориентируется по дирекцион­ному углу, определенному гироскопическим, геодезическим или аст­рономическим способом. С лимба ориентированного прибора считыва­ются непосредственно дирекционные углы на привязываемую точку Р (АР), (ВР) и (СР).

Рис. 16. Прямая засечка ориентированным прибором

Порядок вычисления засечки по таблицам логарифмов аналогичен вычислению засечки по измеренным углам. При этом значения углов α₁, β₁, α₂, β₂, γ₁, γ₂ определяются как разность соответствующих дирекционных углов направлений с исходных пунктов.

Прямая засечка ориентированным прибором вычисляется на ЭКВМ по формулам иного вида, чем при решении засечки по измеренным уг­лам. При этом исключается необходимость вычисления внутренних уг­лов треугольника и время, затрачиваемое на решение задач, значи­тельно сокращается. Найдём эти формулы.

По формулам решения обратной геодезической задачи имеем:

; ,

или У_Р – У_А = (Х_Р – Х_А) tg (АР);

У_Р – У_В = (Х_Р – Х_В) tg (ВР). (19)

Из разности формул (19) имеем

У_В – У_А = Х_Р tg (АР) – Х_А tg (АР) -Х_Р tg (ВР) + Х_В tg (ВР),

откуда . (20)

Получив абсциссу точки Р, по формуле (3.18) определим ординату У_Р:

y_P = (x_P - x_A) tg(AP) + y_A .

Рабочие формулы решения прямой засечки на ЭКВМ по дирекцион­ным углам из двух треугольников будут иметь вид:

;

; (3.21)

y_P = (x_P - x_A) tg(AP) + y_A ;

y_P = (x_P - x_B) tg(BP) + y_B ;

y_P = (x_P - x_C) tg(CP) + y_C .

Если дирекционные углы (АР), (ВР) и (СР) близки к 90 или 270^о, т.е. их тангенсы неограниченно возрастают, целесообразно решать задачу по формулам котангенсов дирекционных углов:

Х_P = (y_P - y_A) tg(AP) + Х_A ;

Х_P = (y_P - y_B) tg(BP) + Х_B ;

Х_P = (y_P - y_C) tg(CP) + Х_C .

Полярной засечкой называется способ определения координат привязываемой точки Р по дирекционным углам (АР), (ВР) и расстояниям и с двух исходных пунктов А и В (рис.17).

Рис. 17. Полярной засечкой

Расстояния измеряют с помощью квантового топографического дальномера КТД-1. Дирекционные углы (АР) и (ВР) определяют гироскопическим или астрономическим способом, если исходные пункты не имеют ориентирных направлений и нет взаимной видимости между ни­ми. Если ориентирные направления или взаимная видимость между ис­ходными пунктами А и В есть, то дирекционные углы (АР) и (ВР) определяют геодезическим способом. В этом случае измеряют углы α и β.

Координаты точки Р вычисляют решением двух прямых геодезических задач. Засечка считается выполненной правильно, если расхождение в коор-динатах точки Р, полученных с пунктов А и В, не превышает 20 м. За окон-чательный результат принимают среднее значение координат, округленное

до 1 м.

ВЫВОДЫ