
Среднее Заочное отделение / 6 семестр / Основы технической эксплуатации сетей телекомуникаций / ОТЭСТ в-6
.pdf
Контрольная работа по дисциплине «Основы технической эксплуатации сетей телекоммуникаций»
Вариант 6
Задание №1 Решить задачу и ответить на теоретический вопрос
Задача
В районе обслуживания АТСК за 6 лет произошло N = 2210 отказов. В 73 случаях связь восстановили за 8.0 ч, в 84 - за 5.0 ч., в 182 - за 3.0 ч., в 213 - за 2.0 ч., 287 - за 1,0 ч., в 531 -
за 0,8 ч., в 840за 0.5 ч. Рассчитать основные показатели надёжности (интенсивность отказов X, среднее время восстановления связей Тв, среднее время наработки на отказ То, коэффициент готовности Кг, вероятность P(t) безотказной работы в интервале t, коэффициент оперативной готовности Rг) для основного периода эксплуатации в интервалы времени, указанные в таблице. Сделать вывод о надёжности и эффективности работы АТСК. Ответить на теоретический вопрос.
Таблица 1 – |
Исходные данные к заданию 1 |
|
|
№ варианта |
|
Заданный интервал времени t, час |
Теоретический вопрос |
6 |
|
4 |
классификация отказа по причинам |
|
возникновения |
||
|
|
|
|
Решение:
Рассчитаем параметр интенсивности отказов по формуле:
|
|
|
|
X = |
|
N |
|
, |
|
|
|||
|
|
|
k |
×ТГ |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
где k – |
количество лет; |
|
|
|
|
|
|
|
|
|
|
|
|
Тг – |
число часов в течении года (Тг = 8760 ч); |
|
|
||||||||||
N – |
количество отказов в течении k лет. |
|
|
|
|
|
|||||||
|
|
X = |
2210 |
|
|
= 0,042отказ/ ч |
|||||||
|
|
6 ×8760 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
Определим среднее время восстановления связей по формуле |
|||||||||||||
|
|
|
|
∑N Tвi |
|
|
∑N tвi |
× ni |
|
||||
|
|
TВ = |
|
i=1 |
|
|
|
= |
|
i=1 |
|
, |
|
|
|
|
N |
|
|
|
N |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
где tвi – |
среднее время восстановления связи для i-го случая; |
||||||||||||
|
ni – |
количество случаев, в которых связь была восстановлена за tвi часов. |
|||||||||||
TВ = 73 ×8 + 84 ×5 +182 ×3 + 213 × 2 + 287 ×1 + 531× 0,8 + 840 × 0,5 = 1,406ч 2210
(1)
(2)
Определим среднее время наработки на отказ по формуле:
1

TO = k ×TГ - TВ × N
N
TO = 6 × 8760 -1,406 × 2210 = 22,38ч 2210
Определим коэффициент готовности по формуле:
|
K Г |
= |
|
TO |
|
|
|
|
TO |
+ TВ |
|
||||
|
|
|
|
|
|||
K Г |
= |
|
22,38 |
|
= 0,94 |
||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
22,38 + 1,406 |
|
|||||
Определим вероятность безотказной работы в интервале времени t по формуле
P(t) = e- X ×t
P(t) = 2,72-0,042×4 = 0,845
Рассчитаем коэффициент оперативной готовности по формуле
RГ = K Г × P(t)
RГ = 0,94 × 0,845 = 0,794
(3)
(4)
(5)
(6)
Исходя из расчетов основных показателей надежности, можно сделать вывод, что данная АТС является надежной. Интенсивность отказов в течении 6 лет равна 0,042 отказ/час. Восстановление связи в ней происходит в среднем в течении 1,406 часа. Вероятность пребывания объекта в работоспособном состоянии в интервале времени 4 часа равна 0,845, а надежность – 0,794. Для улучшения характеристик данной АТС следует провести профилактическое обслуживание, выявить элементы оборудования, которые больше всего подвергаются отказам и произвести их ремонт или замену.
Ответ: X = 0,042 отказ / ч ;TВ = 1,406ч ;TО = 22,38ч ; КГ = 0,94 ; P(t ) = 0,845 ; RГ = 0,794 .
Теоретический вопрос: Классификация отказа по причинам возникновения
По причинам возникновения отказы бывают:
а) Конструктивные – возникшие вследствие ошибок конструктора или несовершенства
методов конструирования, нарушения установленных правил и норм проектирования;
б) Производственные – обусловлены нарушением или несовершенством технологиче-
ского процесса изготовления аппаратуры или ее комплектующих изделий (нарушение установ-
ленных норм при производстве изделия, несовершенство применяемого оборудования);
2
в) Эксплуатационные – возникшие вследствие нарушения установленных правил и норм эксплуатации или от непосредственных внешних воздействий (температура, повышенная влажность, удары, падение, повышение напряжения и т.д.).
3

Задание №2
Задача 1 Оборудование состоит из девяти последовательно соединённых блоков, надежность ко-
торых известна. Найти неисправность методом половинного разбиения и изобразить графически процедуру поиска, при этом изложить суть метода. Данные указаны в таблице 2.
Таблица 2 – Исходные данные к заданию 2 (задача 1)
|
№ варианта |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Надежность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
P1 |
|
|
P2 |
|
P3 |
|
P4 |
P5 |
|
|
P6 |
|
|
P7 |
|
P8 |
|
|
P9 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
6 |
|
|
|
|
|
0,05 |
|
0,06 |
|
0,07 |
|
0,08 |
|
0,09 |
|
|
|
0,1 |
0,2 |
|
0,3 |
|
|
0,05 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Решим данную задачу методом половинного разбиения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
«да» |
|
|
|
|
|
|
|
|
|
«да» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4 |
|
|
|
3 |
|
|
|
4 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
P1=0,05 |
|
P2=0,06 |
|
|
P3=0,07 |
P4=0,08 |
|
|
P5=0,09 |
|
|
P6=0,1 |
P7=0,2 |
|
|
|
|
P8=0,3 |
|
|
P9=0,05 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
«да» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
«нет» |
|
|
|
|
|
|
|
|
|
|
|
«да» |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
«да» |
|
|
|
|
||||||||||||
|
|
|
|
«нет» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 1 – Метод половинного разбиения
Этот метод используется при равенстве времени проверок неисправности элементов и их последовательном соединении. Суть метода состоит в том, что при каждом испытании схема или часть схемы разбивается на две равнонадежные части. При проверки неисправности одной из частей схемы получается ответ – исправна («да») или неисправна («нет») проверяемая часть схемы.
Первое испытание проводится в точке 1, т.к. P1+P2+P3+P4+P5+P6 ≈ P7+P8+P9, т.е. левая и правая части от точки 1 испытания приблизительно равнонадежны.
Второе испытание проводится в левой части (точка 2 после 4 блока), если на выходе 6 блока сигнала нет, или в правой части (точка 2 после 7 блока), если на выходе 6 блока сигнал есть.
Третье и четвертое испытание проводятся после результатов получения предыдущих испытаний аналогичным образом. Иллюстрация решения задачи представлена на рисунке 1.
Пусть неисправен элемент 6.
Тогда выполняем следующие действия:
1)Проверяем сигнал на выходе элемента 6. Сигнала нет.
2)Переводим к проверке сигнала на выходе 4 блока. Сигнал есть.
3)Переводим к проверке сигнала на выходе 5 блока. Сигнал есть.
Следовательно, если на выходе 5 блока сигнал был, а на выходе 6 блока – нет, то неисправен 6 блок.
4

Задача 2 Необходимо найти неисправность в оборудовании, состоящем из пяти параллельных
блоков и среднее время на поиск неисправности в рассматриваемом оборудовании, если известен один из параметров надёжности каждого блока λi и время проверки каждого блока τi:
Описать процедуру поиска неисправности графически.
Таблица 3 – Исходные данные к заданию 2 (задача 2)
№ варианта |
λ1 |
λ2 |
λ3 |
λ4 |
λ5 |
τ1 |
τ2 |
τЗ |
τ4 |
τ5 |
6 |
0,1 |
0,8 |
0,2 |
0,7 |
0,2 |
7 |
2 |
6 |
5 |
10 |
Решение:
Решим задачу методом «время-вероятность». Определим условные вероятности отказа каждого элемента по формуле:
|
|
|
qi = |
|
|
λi |
(7) |
||||||
|
|
|
∑i5=1 λi |
|
|||||||||
q = |
|
|
0,1 |
|
|
|
|
|
= |
0,1 |
= 0,05 |
||
|
+ 0,8 |
+ 0,2 + 0,7 + 0,2 |
|
||||||||||
1 |
0,1 |
2 |
|
||||||||||
|
|
||||||||||||
|
|
|
q2 |
= |
0,8 |
= 0,4 |
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
q3 |
= |
0,2 |
= 0,1 |
|
|
|
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|||
q4 = 0,7 = 0,35 2
q5 = 0,2 = 0,1 2
Определим отношение времени к вероятности для каждого блока.
τ1 = |
|
7 |
= 140 |
||||
0,05 |
|||||||
q1 |
|
|
|||||
τ 2 |
= |
|
2 |
|
= 5 |
||
|
|
|
|||||
q2 |
0,4 |
|
|||||
τ 3 |
= |
6 |
= 60 |
||||
|
|
||||||
q3 |
0,1 |
|
|
||||
τ 4 = |
|
5 |
= 14,3 |
||||
0,35 |
|||||||
q4 |
|
|
|||||
5
τ 5 = 10 = 100 q5 0,1
Определим оптимальную последовательность проверки по формуле:
τ i+1 £ τ i |
(8) |
qi+1 qi
Тогда оптимальная последовательность проверки будет следующая
min ¬ τ 2 |
< τ 4 |
< τ 3 |
< τ 5 |
< τ1 |
(9) |
q2 |
q4 |
q3 |
q5 |
q1 |
|
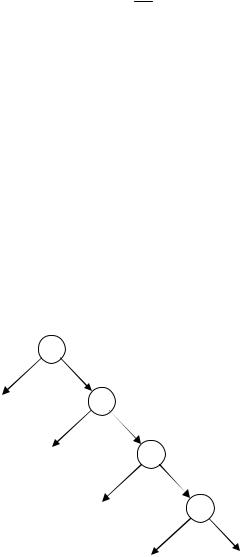
Опишем процедуру поиска неисправности графически
|
«нет» |
|
2 |
«да» |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|||
|
2 |
|
«нет» |
«да» |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||
|
|
|
4 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
«нет» |
|
|
«да» |
||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
«нет» |
|
|
||
|
|
|
|
|
|
|
|
|
|
«да» |
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||
Рисунок 2 – |
Реализация метода «время-вероятность» |
|||||||||||||
Поиск неисправности начинаем со 2 элемента. Если он исправен, переходим к проверке 4 элемента и т.д.
Определим среднее время на поиск неисправности по формуле:
TПН = q1 ×(τ 5 +τ3 +τ 4 +τ 2 ) + q5 ×(τ 5 +τ3 +τ 4 +τ 2 ) + q3 ×(τ 3 +τ 4 +τ 2 ) + q4 ×(τ 4 +τ 2 ) + q2 ×τ 2 (11)
TПН = 0,05 × (10 + 6 + 5 + 2) + 0,1× (10 + 6 + 5 + 2) + 0,1× (6 + 5 + 2) + 0,35 × (5 + 2) + 0,4 × 2 = 8,0мин
Допустим, что в схеме присутствует неисправность блока 5.
Эту неисправность мы распознаем после того, как проверим 2 блок, затем 4, после этого 3 и только потом 5.
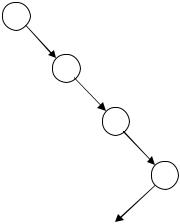
Опишем процедуру поиска неисправности в четвертом блоке графически
6
2
«да» |
|
|
|
|
|
|
|
4 |
«да» |
|
|
||
|
|
|
|
|||
|
|
3 |
«да» |
|||
|
|
|
|
|
||
|
|
|
«нет» |
5 |
||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
||||
Рисунок 3 – Неисправность 5 блока |
||||||
Ответ: ТПН = 8,0 мин; min ← τ 2 |
< τ 4 |
< τ 3 |
< τ 5 |
< τ1 . |
||
q2 |
q4 |
|
q3 |
q5 |
q1 |
|
7
Задание №3 |
|
|
Выполнить теоретическое задание, |
согласно варианта, приведенному в таблице |
|
4. |
|
|
Таблица 4 – Исходные данные |
|
|
|
|
|
№ варианта |
|
Задание |
|
|
|
6 |
Основное назначение ремонтной группы, обслуживающей передатчики ра- |
|
|
диовещания |
|
|
|
|
|
|
|
Ответ:
Основными задачами ремонтной группы, обслуживающей передатчики являются:
-своевременный выезд бригады на объект с целью выяснения причин неисправности оборудования;
-установление наличия неисправности;
-устранение неисправности, своевременный ремонт и настройка передатчиков;
-проверка работоспособности аппаратуры после ремонта;
-обеспечение бесперебойной, эффективной и высококачественной работы передатчи-
ков
-поддержание в норме электрических характеристик оборудования передатчиков;
-поддержание безошибочной работы программного обеспечения передатчиков радио-
вещания;
Ответственность за выполнение данных мероприятий возлагается на руководителя ре-
монтной группы, осуществляющих эксплуатацию радиопередатчиков.
8
Список использованных источников
1Конспект лекций.
2Берганов И.Р. и др. Проектирование и техническая эксплуатация систем передачи. -
М.: Радио и связь, 1989 3 Векша Т.А. Концепция технической эксплуатации сетей электросвязи: Учебное посо-
бие. - Вт.: ВФ УО «ВГКС», 2004 4 Векша Т.А. Основные параметры системы технической эксплуатации: Учебное посо-
бие. - Вт.: ВФ УО «ВГКС», 2004
9
