4.3 Майбутня і сучасна вартість ануїтету

Фінансові операції, що припускають щорічний рівний внесок (або отримання) коштів заради накопичення визначеної суми в майбутньому звичайно називають ануїтетами (англ. annuity – щорічна рента). Класичним прикладом такого роду операцій є накопичення амортизаційного фонду, тобто грошового фонду, що дозволяє придбати нове обладнання замість старого, яке поступово зношується.

Для того, щоб амортизаційні відрахування зіграли свою роль, менеджери повинні точно знати, якою сумою вони будуть розпоряджатися в кінцевому рахунку (у майбутньому) при визначених сумах відрахувань у даний час. Необхідні розрахунки в принципі можна зробити за допомогою формули (4.1), але можна вирішити цю задачу і менш трудомістким способом.

Щоб зрозуміти зміст такого розрахунку розглянемо приклад. Припустимо, підприємство буде вносити щорічно (наприкінці року) на спеціальний амортизаційний рахунок у банку 1 млн. грн. за річною ставкою по депозиту 16 %. Необхідно визначити, якою сумою воно буде розпоряджатися через три роки.

Очевидно, що перший мільйон гривень пролежить у банку, заробляючи відсотки, два роки, другий  рік, третій  анітрошки (з погляду заробляння відсотків). За допомогою формули розрахунку майбутньої вартості (6.1) можна знайти ту величину, до якої встигне зрости кожний із внесків до моменту вилучення загальної суми з рахунка. А потім, склавши ці суми, знайдемо остаточну величину внеску, яким будемо розпоряджатися через три роки. Такий підхід називають визначенням майбутньої вартості ануїтету. Результати розрахунку запишемо в таблиці 4.2.

Таблиця 4.2

Розрахунок майбутньої вартості ануїтету.

Номер щорічного платежу	Час, протягом якого заробляється процентний доход, років	Майбутня вартість річного внеску, млн. грн.
1	2	1. 00(1+0. 16)2=1,346
2	1	1. 00(1+0. 16)1=1,160
3	0	1. 00(1+0. 16)0=1,00
Разом майбутня вартість ануїтету 3, 506

Якщо зобразити цю схему розрахунку у виді універсальної моделі, то одержимо рівняння

, (4.6)

де C_fn  майбутня вартість ануїтету за n періодів, грн.;

P_t  платіж, здійснюваний наприкінці періоду t, грн.;

k  рівень доходу (ставка дисконтування), долі одиниці;

n  число періодів, протягом яких надходить доход, од. часу.

Якщо суми платежів однакові в кожнім періоді, то це рівняння можна переписати в іншому виді:

(4.7)

Оскільки всі платежі однакові по величині, то рівняння це буде справедливим, хоча воно як би змушує платежі першого і останнього років помінятися місцями, оскільки тут платіж першого року з номером t=1 не приносить доходу взагалі, а платіж останнього року, для якого t=n і який у дійсності не приносить ніякого доходу, за цією формулою працює на приріст доходу довше всього. Таке спрощення, що не спотворює результату розрахунку, дозволяє ще більш спростити формулу розрахунку ануїтету.

Результатом такого спрощення стане наступне рівняння

, (4.8)

де A1^f_{n, k}  стандартна майбутня вартість ануїтету в одну гривню наприкінці кожного періоду одержання доходів протягом n періодів і при ставці доходу (ставці дисконту) на рівні k, що розраховується по формулі

(4.9)

Такий ануїтет звичайно називають рівневим чи стандартним (або ануїтет-фактором) . Наростання сум при стандартному (одна гривня) ануїтеті можна визначити за допомогою калькулятора чи спеціальних таблиць. Для визначення майбутньої вартості ануїтету необхідно помножити отриманий коефіцієнт на річну суму грошового потоку.

Основою всіх розрахунків, які проводяться при обґрунтуванні й аналізі інвестиційних проектів, є зіставлення витрат, які необхідно здійснити сьогодні, і тих грошових надходжень (обумовлених зворотних грошових потоків), які можна одержати в майбутньому.

У рішенні цієї проблеми допомагає підхід, що пропонує визначення поточної (сучасної, дисконтованої) вартості ануїтету. На цій основі досить чітко можна представити, наскільки окупляться сьогоднішні вкладення коштів майбутніми доходами. Зрозуміти зміст такого аналізу легше на конкретному прикладі інвестиційного проекту, що пропонує одержання 1 млн. грн. наприкінці кожного з трьох років. Приведену вартість виходячи зі ставки дисконтування на рівні 0.16 для кожного з майбутніх припливів грошей можна визначити за формулою (4.3). Отримані результати зведемо в табл. 4.3.

Таблиця 4.3. Розрахунок поточної вартості ануїтету

Роки	Зворотні грошові потоки (надходження доходів), млн. грн.	Сучасна вартість майбутніх грошових доходів, млн. грн.
1	1. 000	1, 0/(1+0,16 )1 = 0,862
2	1. 000	1, 0/(1+0,16)2 = 0,743
3	1. 000	1, 0/(1+0,16)3 = 0,641
Разом сучасна вартість ануїтету =2,246

Логіка такого перерахунку буде незмінною для будь-якого числа років надходження коштів, як наслідок використання об’єкту, створеного в результаті інвестицій. Звідси можна вивести загальну формулу розрахунку приведеної сучасної вартості ануїтету

, (4.10)

де C_pn – майбутня вартість ануїтету, грн.;

Р_ft  майбутнє надходження коштів наприкінці періоду t, грн. ;

k  необхідна норма прибутковості по інвестиціях (долі одиниці);

n  число періодів, протягом яких у майбутньому надійдуть доходи від сучасних інвестицій.

У випадку, якщо платежі по ануїтету однакові в кожнім періоді формулу (6.8) можна спростити і представити в наступному виді

_, (4.11)

де  стандартна сучасна вартість ануїтету в 1 грн. наприкінці періоду n років при ставці річної прибутковості на рівні k:

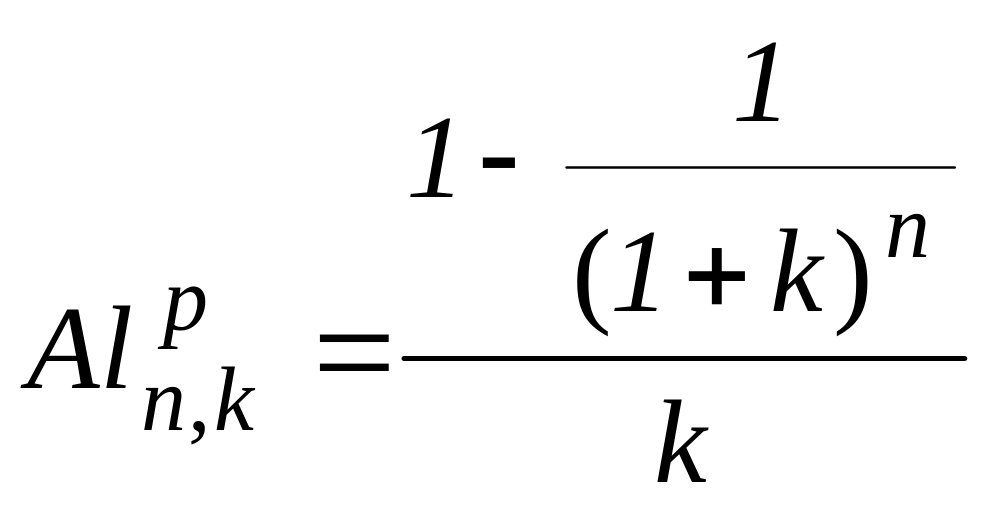(4.12)

Отримане вираження можна перетворити, помноживши чисельник і знаменник на (1+k)ⁿ

(4. 13)

Знайти потрібне значення стандартної сучасної вартості ануїтету в 1 грн. – можна за допомогою електронного калькулятора чи по спеціальних довідкових таблицях, звичайно прикладених до довідково-методичних посібників по ефективності інвестицій, а знайшовши цей коефіцієнт за формулою (4.12) легко визначити поточну (сучасну) вартість ануїтету.

У цілому, резюмуючи вищевикладене, можна виділити кілька основних принципів, яких слід дотримуватись при оцінці будь-якого виду інвестицій:

а) варто вести розрахунки в грошах однакової цінності, приводячи усі витрати і результати (усі грошові потоки) до єдиної дати в сьогоденні (або в майбутньому);

б) оцінку інвестицій необхідно проводити з огляду їхньої можливості заробити для інвестора доход не менший, ніж забезпечують альтернативні, реально існуючі, доступні інвестору способи вкладення коштів;

в) у загальному випадку вибирати слід ті інвестиції, при яких суми зворотних грошових надходжень будуть перевищувати суми грошових витрат, якщо ті й інші виразити в грошах однакової вартості (тобто приведених до єдиної дати).