Санкт-Петербургский Государственный Университет Телекоммуникаций
имени проф. М.А. Бонч-Бруевича.
ТЭС
Курсовая работа: “Расчет основных характеристик системы передачи информации”
Вариант № 76
Санкт – Петербург
2005 г.
ЗАДАНИЕ
Рассчитать основные характеристики системы передачи информации, структурная схема которой дана на рисунке:
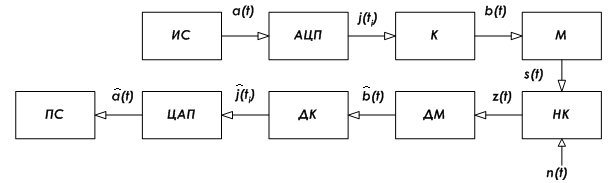
Элементы системы передачи информации:
ИС – источник непрерывного сообщения а(t);
АЦП – аналого-цифровой преобразователь, преобразует сообщение в отсчеты а(ti), квантованные уровни аj(ti) и соответствующие им числа j(ti) – номера уровней,затем образует модулирующий сигнал b(t);
К – кодер, выполняет помехоустойчивое кодирование сигнала b(t);
М – модулятор, создает высокочастотный аналоговый сигнал s(t);
НК – непрерывный
канал, на выходе которого образуется
аддитивная смесь z(t)
сигнала с помехой
;
ДМ – демодулятор,
восстанавливает передаваемый сигнал
,
в результате получают сигнал
,
который может содержать ошибки;
ДК – декодер, обнаруживает ошибки в принятом сигнале
ЦАП – цифро-аналоговый
преобразователь, декодирует сигнал
,
получая номера передаваемых уровней
;
затем восстанавливает квантованные
уровни аj(ti)
и непрерывное сообщение
;
ПС – получатель сообщения.
Исходные данные
№ вар |
76 |
Уровень, а мин, В |
-6,4 |
Уровень, а макс, В |
+6,4 |
Верхняя частота, fв, Гц |
8·103 |
№ уровня, j |
105 |
Вид модуляции |
ФМ |
Энерг. спектр помехи,N0, В2/Гц |
8,15·10-7 |
Способ приема |
1 (оптимальный когерентный прием) |
1. ИСТОЧНИК СООБЩЕНИЙ
Источник создает непрерывное сообщение a(t) – случайный квазибельный стационарный процесс, мощность которого сосредоточенна в области нижних частот, в полосе частот от 0 до fв. Мгновенные значения сообщения равновероятны в интервале от amin до amax.
Функция распределения F(х) мгновенных значений сообщения а(t), плотность распределения wа(x) и построить их графические изображения.
Для отыскания плотности распределения wа(х) сообщения учтем, что все мгновенные значения сообщения равновероятны в интервале от amin до amax
В
Внутри интервала плотность определяется из условий нормировки, вне его равна 0.
Аналитическое выражение для плотности вероятности wа(х), с учетом того, что все мгновенные значения данного случайного процесса в равновероятны, можно записать так:
Здесь С – это константа, её значение можно определить из условия нормировки:
-
условие нормировки
=C(amax-amin)=1
Из этого следует:
C=
В-1
С учетом этого аналитическое выражение для плотности вероятности wа(х):
График плотности распределения имеет вид:
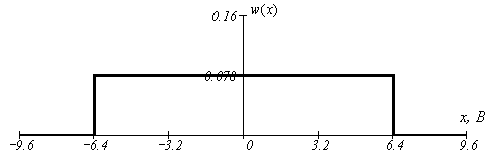
Аналитическое выражение для функции распределения вероятности Fа(х):
А график функции распределения имеет вид:
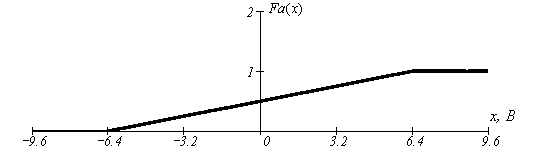
1.2 Расчет математического ожидания m{a(t)} и дисперсии D{a(t)} сообщения a(t).
Математическое ожидание определяется по формуле:
Дисперсия случайного процесса D{а(t)}:
