
- •Вопросы дозиметрии инкорпорированных нуклидов
- •Источники внутреннего облучения
- •Распределение активности естественного происхождения в аэрозольных частицах различных размеров
- •Размеры и скорости осаждения аэрозольных частиц
- •4.2.1.Тканевая доза, обусловленная излучением инкорпорированных радиоактивных нуклидов
- •Дозовые функции точечных изотропных источников в бесконечной тканеэквивалентной среде
- •Оценка поглощенной энергии на основании схем распада нуклидов
- •Кинетика продуктов распада радона на фильтре
- •4.1. Определение удельной активности источников
- •Определение удельной активности толстослойных источников β – излучения
- •Количественная трековая авторадиография β–активных “горячих“ частиц
- •Преобразования источников различной конфигурации в бесконечной среде
4.1. Определение удельной активности источников
α – излучения
Траектории α–частиц в веществе практически прямолинейны, и величина их пробега Rα , например, в воздухе в зависимости от энергии Тα (МэВ) определяется соотношением:
![]() ±10%,
(см);
±10%,
(см);
В других веществах пробег частиц оценивается следующим образом:
![]() ,
где
,
где
![]() (рi
– весовая
доля атомов с весом Аi).
(рi
– весовая
доля атомов с весом Аi).
Для тонкого плоского источника с равномерно распределенными изотропными источниками α–частиц зависимость числа прошедших частиц N(x)через плоский фильтр толщиной х через ед. площадь определяется зависимостью
![]() ,
,
где S – число частиц источника, выходящих с ед. его поверхности (рис.Н).
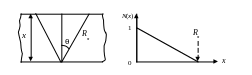
Рис.Н. Геометрии расчета.
Если в плоском слое вещества с толщиной больше Rα равномерно распределен нуклид с удельной активностью А (Бк/см3) излучающий моноэнергетические α – частицы, то из из слоя на глубине x через поверхность источника выходит
![]() .
.
Полное число частиц
![]() ,
выходящих с ед. поверхности источника,
,
выходящих с ед. поверхности источника,
![]() .
.
Определение удельной активности толстослойных источников β – излучения
Выход β – частиц с поверхности толстослойного источника есть величина, определяющая число частиц, выходящих с единицы площади поверхности источника в единицу времени, пропорциональная удельной активности источника. Практически необходимо количественно связать скорость счета N детектора (счетчика) с величиной удельной активности q препарата (объекта):
![]() ,
,
что следует из
соотношения:
![]() ,
где
,
где
n0 – выход β – частиц с единицы поверхности источника с единичной удельной активностью,
S – площадь поверхности источника,
К – поправка на поглощение частиц на пути от поверхности источника до детектора,
ω – доля вышедших из источника частиц, попадающих в счетчик.
Обычно известна величина площади поверхности источника S и параметр к определяется экспериментально; кроме того, необходима информация об угловом распределении выходящих из источника частиц для определения параметра ω, и основная величина n0, зависящая от энергетического спектра β – частиц и атомного номера вещества источника. Соответствующая связь между значением удельной активности источника и выходом β – частиц с его поверхности может быть получено (в предположении независимости коэффициента обратного отражения β – частиц от их энергии) следующим образом: рассматривается бесконечная однородная среда (максимальный пробег электронов значительно меньше линейных размеров среды), каждый элемент объёма которой испускает электроны с энергией Е. На рис. Н показаны три геометрии, в рамках которых последовательно проводится вывод соответствующего соотношения. Определим средний путь l частиц, пересекающих слой dx. В геометрии 1 угловое распределение частиц является изотропным и ток частиц через любую плоскость в среде ~ cosθ (dl = dx/cosθ).
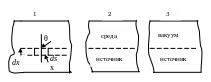
Рис.Н. Геометрии расчета.
Число частиц dn',
пересекающих площадку ds,
в единицу
времени в единичном телесном угле
![]()
![]() ,
где n'
-
полное число частиц, пересекающих ds.
Среднее
расстояние l
частиц, проходящих через слой dx:
,
где n'
-
полное число частиц, пересекающих ds.
Среднее
расстояние l
частиц, проходящих через слой dx:
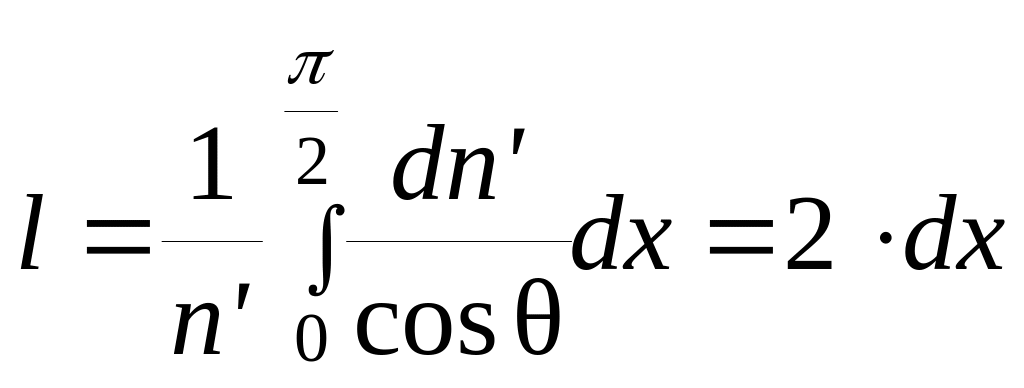 .
.
Если Е1 энергия электронов, испущенная в элементе объёма dv = dsdx,и Е2 – поглощенная энергия в том же объёме, то
![]() и
и
![]() ,
где
,
где
![]() –
средние ионизационные
потери энергии электронов
–
средние ионизационные
потери энергии электронов
в веществе, где равномерно распределен моноэнергетический источник электронов. В условиях бесконечной геометрии Е1 = Е2,, откуда следует:
![]() .
(ф2)
.
(ф2)
В приближении
![]() ,
где R
– средний
пробег электронов с энергией Е,
соотношение (ф2) преобразуется к виду:
,
где R
– средний
пробег электронов с энергией Е,
соотношение (ф2) преобразуется к виду:
![]() .
(ф3)
.
(ф3)
С учетом геометрии 2, где в верхнем полупространстве среды источники отсутствуют (в итоге источников вдвое меньше), соотношение (ф3) принимает вид:
![]() .
(ф4)
.
(ф4)
(последнее соотношение определяет связь между величиной удельной активности и выходом α – частиц.
В геометрии 2 эффект обратного отражения электронов (альбедо) от верхнего полупространства (вклад от верхнего полупространства был просто исключен). Если коэффициент обратного отражения электронов р (р < 1), то с учетом возможности многократного пересечения электронами плоскости раздела в геометрии 2
![]() ,
где n
соответствует
выходу частиц в геометрии 3; в последнем
случае геометрия 3 определяет реальные
условия измерения выхода электронов
из источника:
,
где n
соответствует
выходу частиц в геометрии 3; в последнем
случае геометрия 3 определяет реальные
условия измерения выхода электронов
из источника:
![]() .
(ф5)
.
(ф5)
Если источники в среде являются β – излучающими нуклидами с непрерывным энергетическим распределением n(E), то в соотношении (ф5) величина пробега R заменяется усредненной по спектру n(E) зависимости R(E) (имеет место однозначная связь пробега электрона с его энергией):
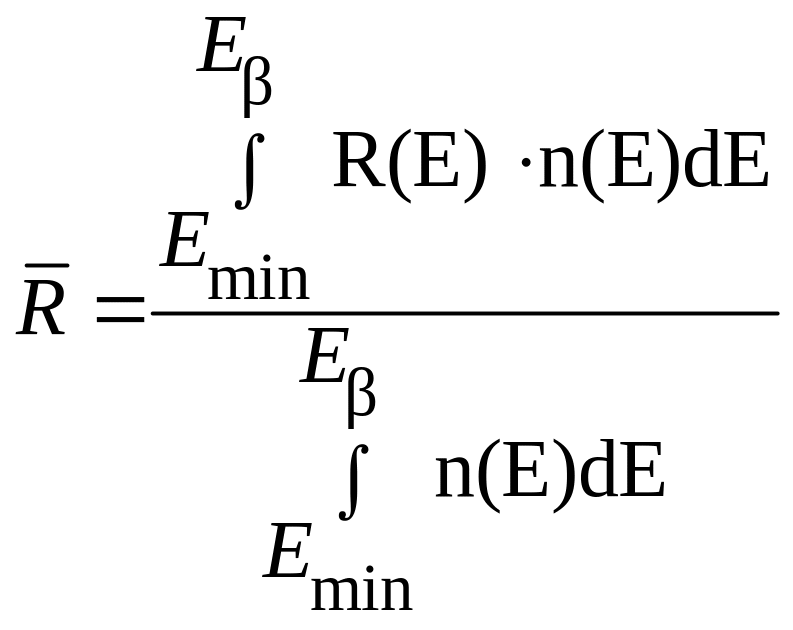 ,
где (ф)
,
где (ф)
![]() -
граничная энергия β
– спектра. Используется также приближение
-
граничная энергия β
– спектра. Используется также приближение
![]() средняя
энергия β – спектра.
средняя
энергия β – спектра.
Соотношение для оценки удельной активности β – нуклидов
на основании функции ослабления частиц β – спектра.
Пусть q
– удельная
активность β
– нуклида
в среде с плотностью ρ. Из 1 см3
изотропно
излучается qρ
частиц в сек. На глубине х
от поверхности
источника выделим объём dV
= s·dx,s
– площадь источника. В относительный
телесный угол ω испускается
![]()
частиц и при 100% эффективности регистрации скорость счета от выделенного элемента объёма
![]() ,
где
,
где
μ – коэффициент ослабления β –частиц. Полное число частиц, регистрируемое детектором
![]() .
.
