Кинетика продуктов распада радона на фильтре

Распад двух нуклидов

Имеется два нуклида, первый из которых – материнский нуклид;при его распаде образуется второй нуклид – дочерний (рис. цц)

Рис. цц. Радиоактивный распад связанных нуклидов

Система дифференциальных уравнений, соответствующая приведенной выше схеме связанных нуклидов следующая:

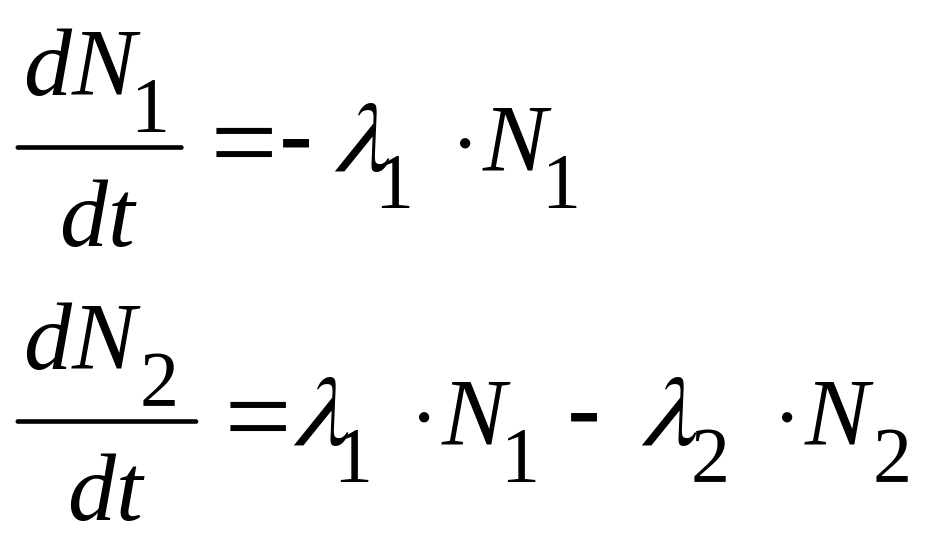(6.6)

где N₁ и N₂ – количество нуклидов,

λ₁ и λ₂ – соответствующие постоянные распада, с^-1.

При начальных условиях t = 0: N₁ = N₀₁ и N₂ = N₀₂ решение системы имеет вид:

.

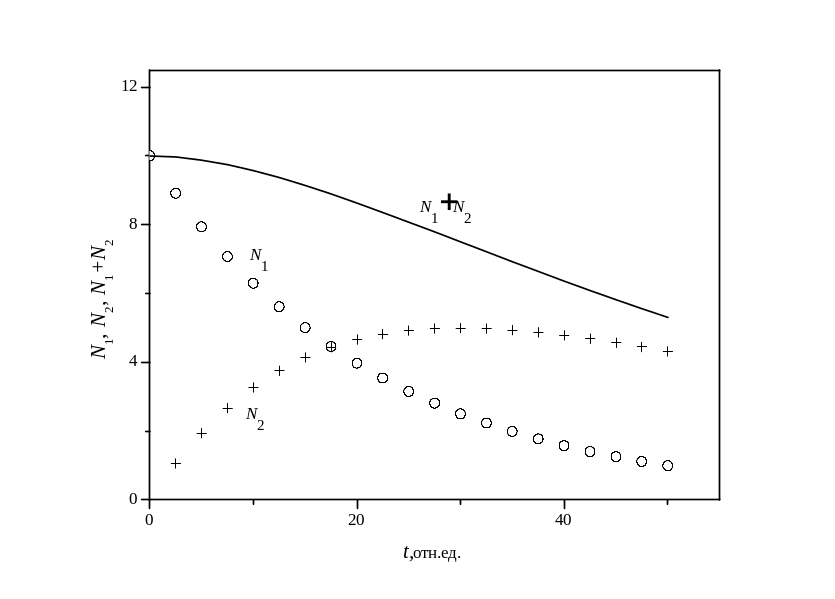
На рис. ИИ показано изменение количества нуклидов N₁ и N₂ от времени; начальное значение дочернего нуклида при t = 0 N₀₂ = 0.

Некоторые частные случаи:

а) долгоживущий материнский нуклид и короткоживущий дочерний, т.е. λ₁ << λ₂ (напр., ²²⁶Ra (T_1/2  1622 года) → ²²²Rn (3,8дня)); решение (6.6) при t = 0 и N₀₂ = 0 преобразуется к соотношению:

;

при условии t→ ∞, .

б) при соотношении λ₁ >> λ₂ и начальном состоянии t = 0 и N₀₂ = 0

.

Для первого случая при t→ ∞, следует ; если имеется цепочка из более чем двух нуклидов, то . Это условие т.н. радиоактивного равновесия (или векового равновеия).

Воздух содержит радон с его продуктами распада. Эта смесь прокачивается через фильтр со скоростью w; эффективность фильтра предполагается равной единице:η = 1. Накопление дочерних продуктов распада учитывается в соответствии со следующей частью цепочки распада ²²²Rn (указаны периоды полураспада и вид излучаемых частиц):

α β β,α

RaA ─→ RaB ─→ RaC ─→ RaD

~ 3,1 мин. ~ 26,8 мин. ~ 19,9 мин. ~ 22 года.

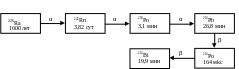
Рис. Упрощенная цепочка распада ²²²Rn

Конечной целью процедуры прокачки и последующего радиометрического определения значений активностей на фильтре является оценка удельной концентрации дочерний продуктов распада ²²²Rn в воздухе.

Если N_а, N_b ,N_c – число атомов RaA, RaB, RaC (в виде аэрозолей), осевших на фильтре за время t, и n_a, n_b ,n_c концентрация соответствующих атомов в воздухе, то система дифференциальных уравнений, определяющих кинетику атомов на фильтре, имеет вид:

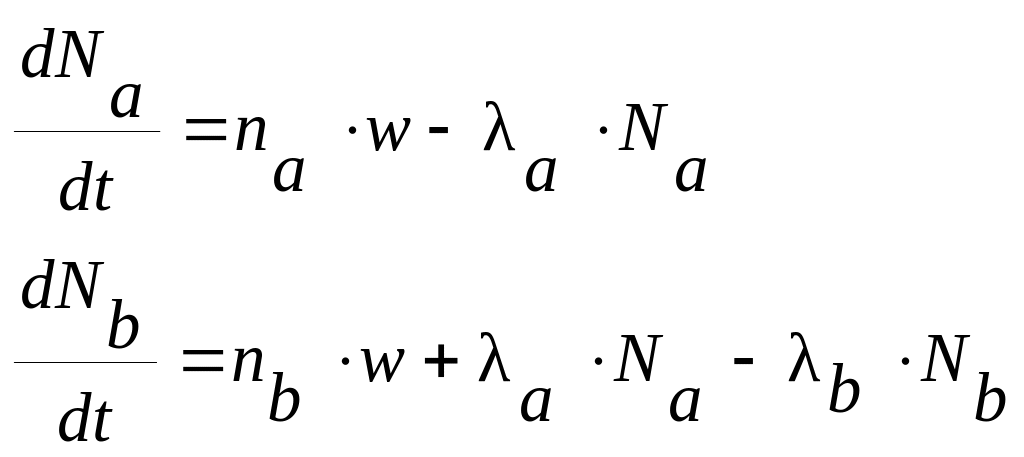(1.1)

,

где, λ_a, λ_b, λ_c,– постоянные распада трех нуклидов.

При начальных условиях: t = 0, N_а, N_b, N_c = 0 решение системы (1.1) следующее:

,

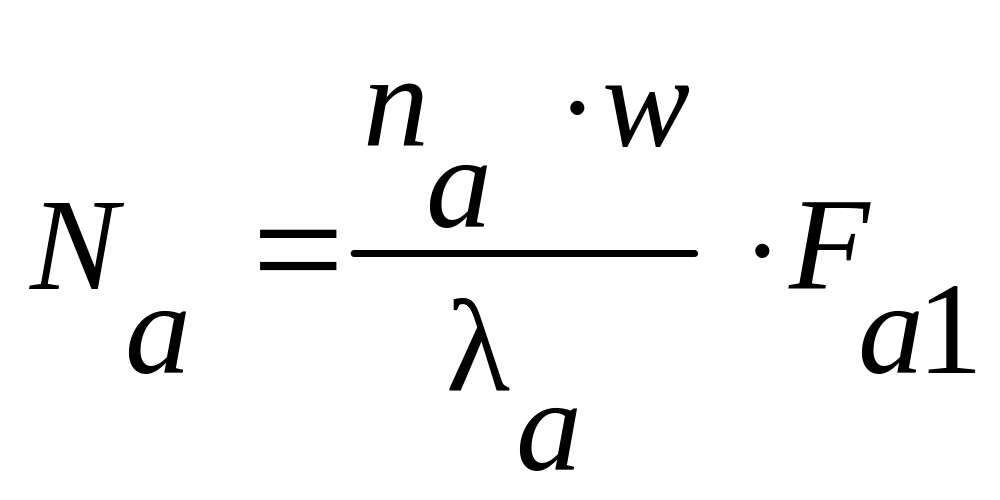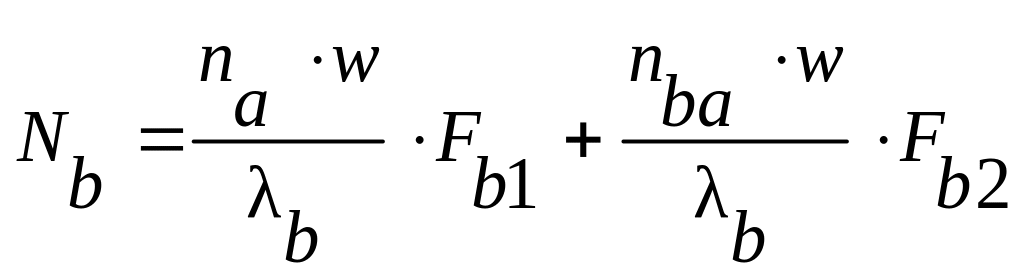, (1.2)

,

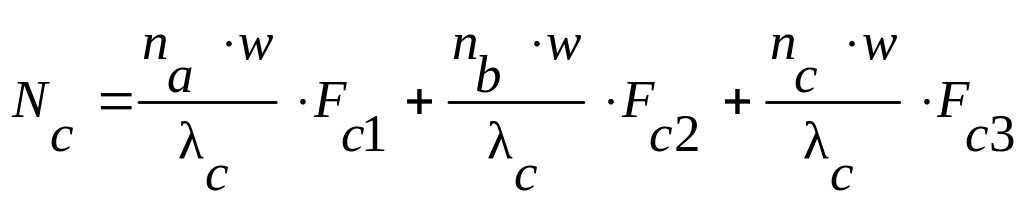где , , , , , – функции времени t и постоянных распада :

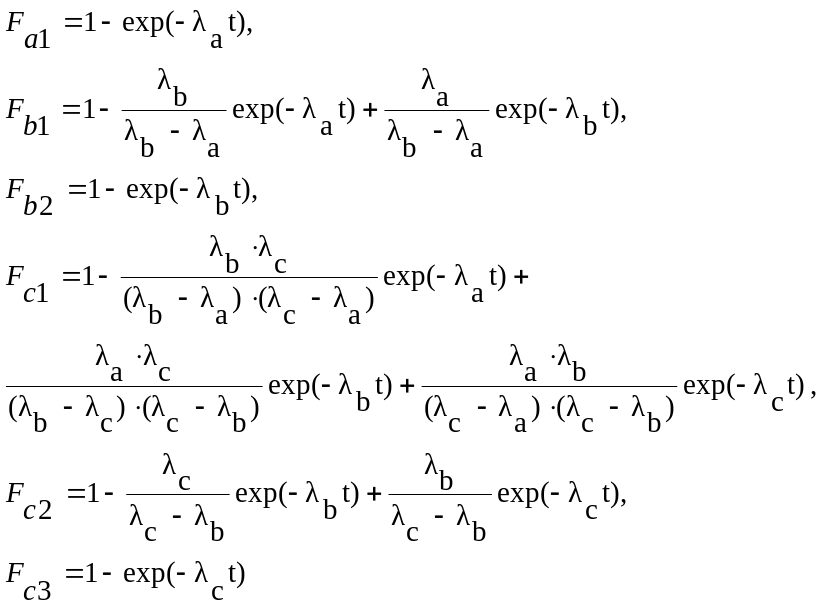(1.3)

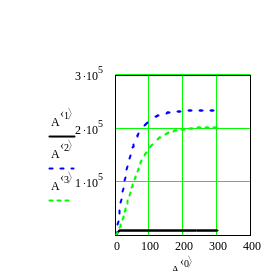
Рис. Зависимость числа атомов на фильтре от времени.

Соответствующие величины активностей

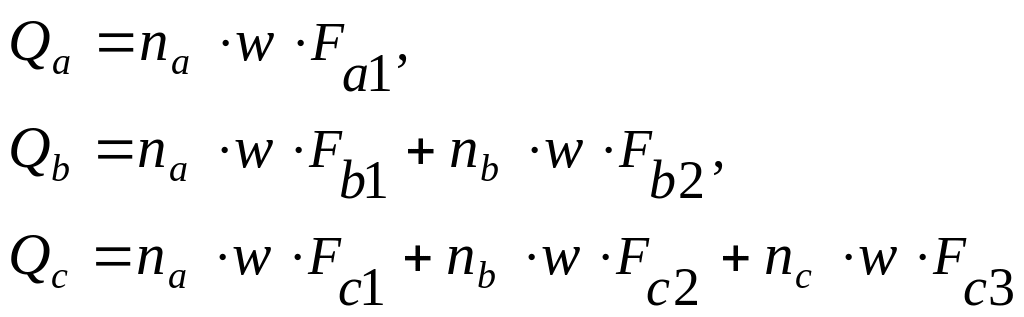(1.4)

При t → ∞ значения функций и

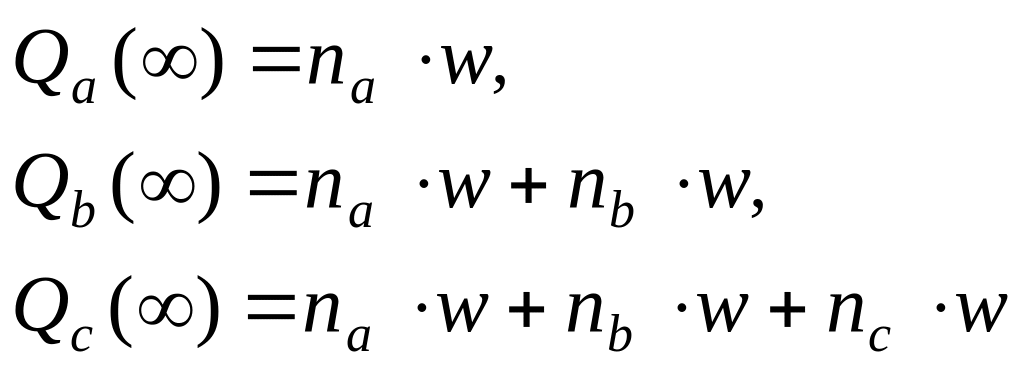(1.5)

С учетом распада RaC полная активность и

(1.5)

При равновесии продуктов распада ²²²Rn в воздухе и .

, откуда следует:

и

При раздельном режиме измерении α – или β – активности из схемы распада следует:

→ β – активность, → α – активность;

и

.

При равновесии дочерних продуктов распада ²²²Rn

по измеренным величинам активностей и однозначно определяется значение и, соответственно, n_a, n_b ,n_c:

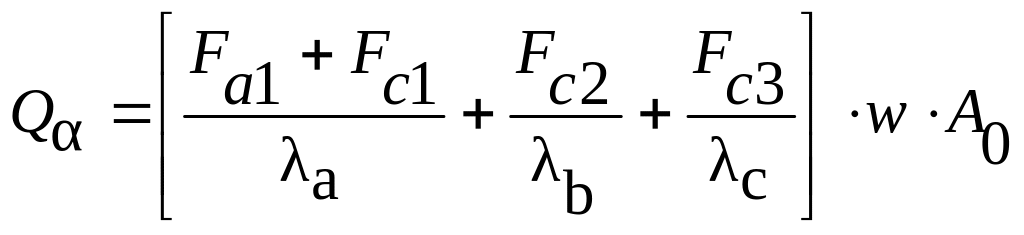
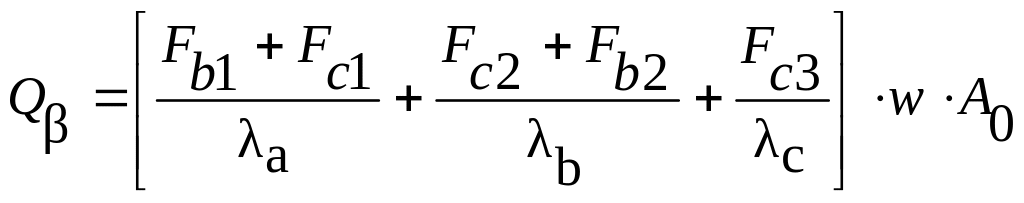_(1.6)

Из соотношений (1.6) может быть рассчитана зависимость

;

Значение этого отношения при t → ∞ и при условии равновесия:

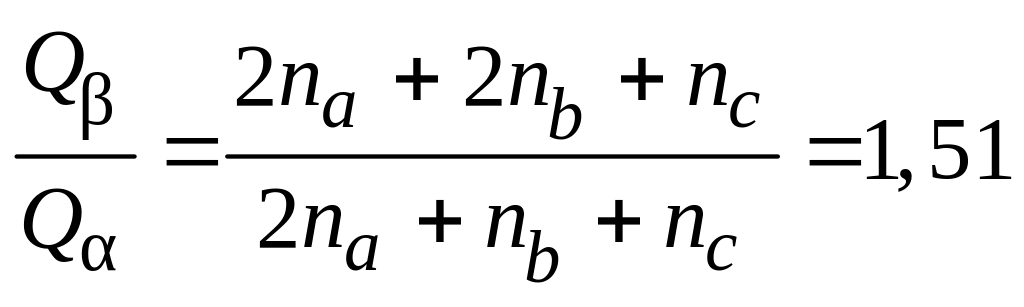_(1.7)

В крайнем случае неравновесия (присутствует только RaA)

1

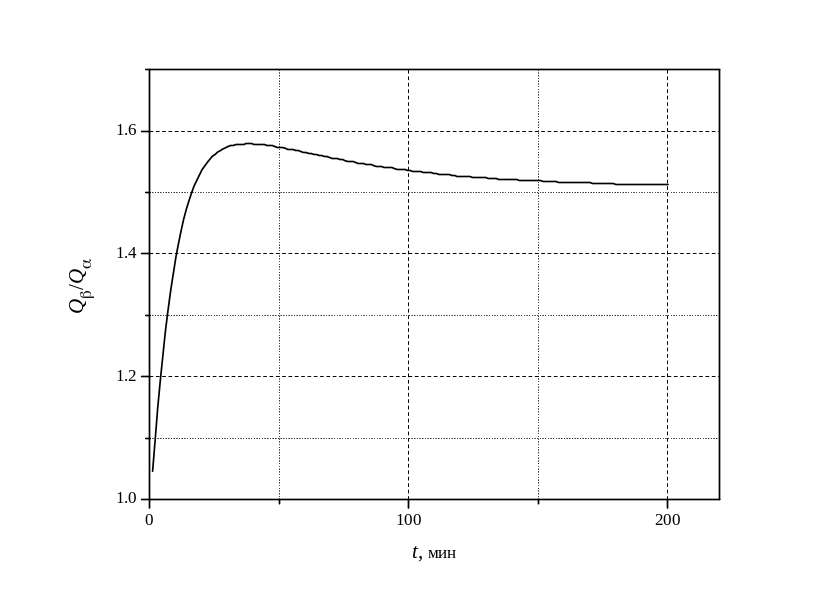
Рис. Зависимость отношения активностей от времени

Кинетика продуктов распада ²²²Rn на фильтре после процесса

прокачки

После окончания прокачки воздуха изменение количества ранее накопленных радионуклидов соответствует системе уравнений:

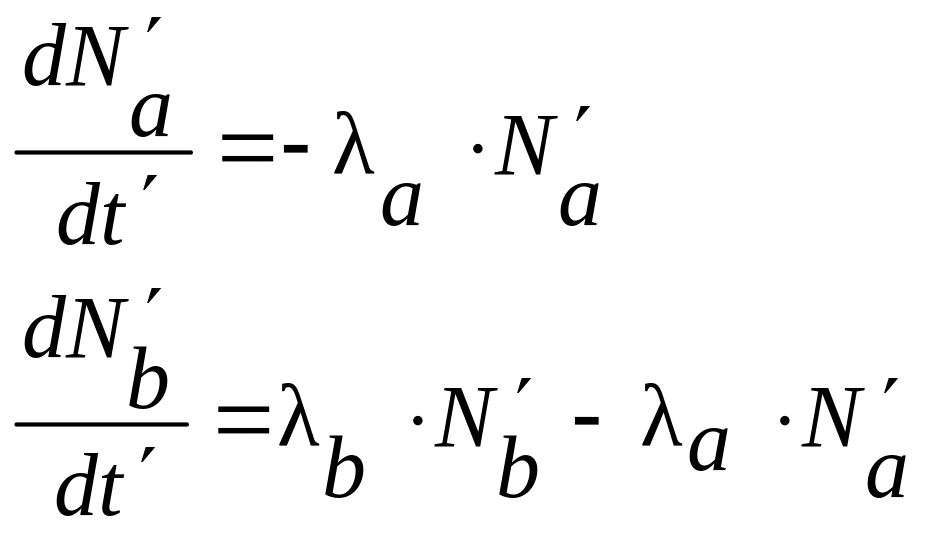(1.8)

.

Начальные условия при :

, где t - время прокачки. Решение системы (1.8) есть функции параметров, , λ_a, λ_b, λ_c, , N_а(t), N_b(t), N_c(t):

;

;

.

Величины α – и β – активности через время выдержки соответственно равны:

;

Измерение концентрации аэрозолей с долгоживущими нуклидами на фоне короткоживущих нуклидов

Самый распространенный способ – выжидание, т.е. активность фильтра измеряется через некоторое время, достаточное для распада короткоживущих аэрозолей.

Если А_Т – активная концентрация долгоживущего аэрозоля (воздушная среда), Q_T – соответствующая активность, то за время t

,

где η – эффективность фильтра, w – скорость прокачки воздуха.

, (1)

где n – концентрация короткоживущих нуклидов в воздухе,

и - постоянная и период полураспада нуклида.

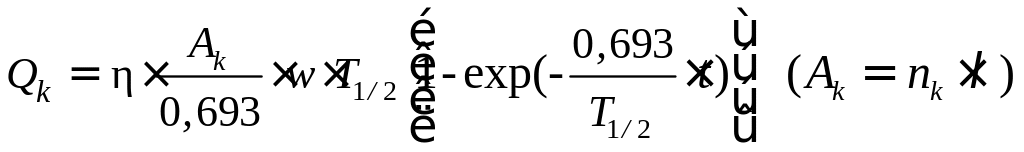(2)

Из соотношений (1), (2) следует:

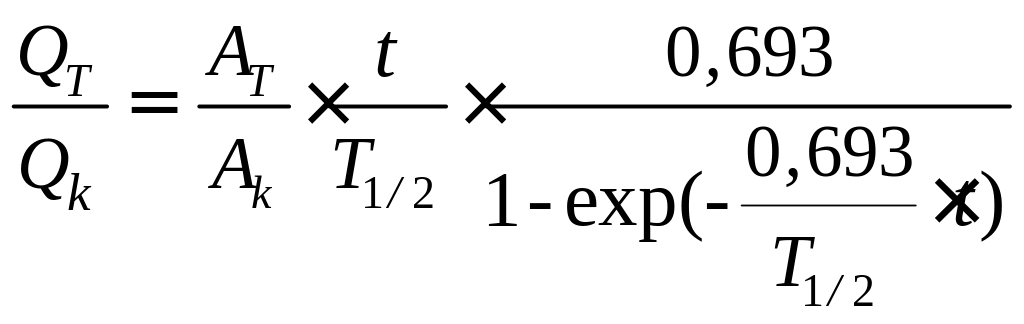(3)

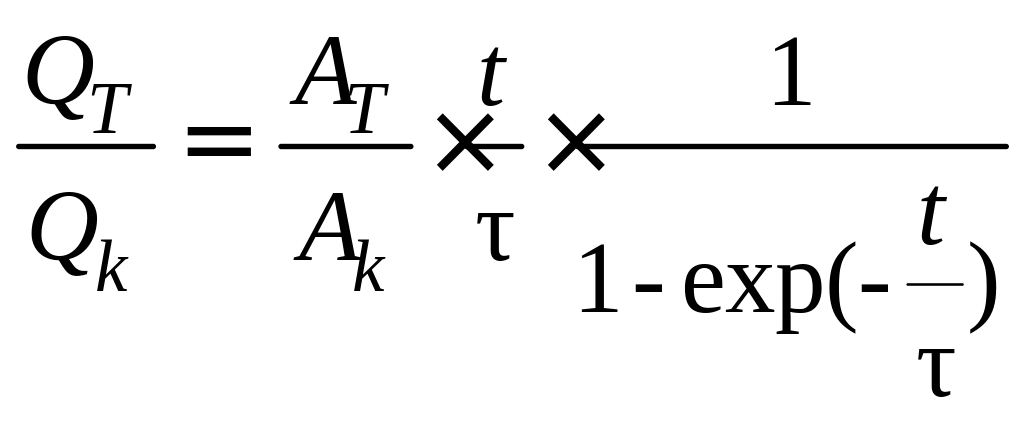
(4)

а) время прокачки мало, т.е. t/τ << 1:

.

б) длительное время прокачки t >> τ:

.

После прокачки активность долгоживущих нуклидов незначительно изменяется относительно короткоживущих, т.е.

где - время после прокачки. Отношение активностей после времени :

Отсюда

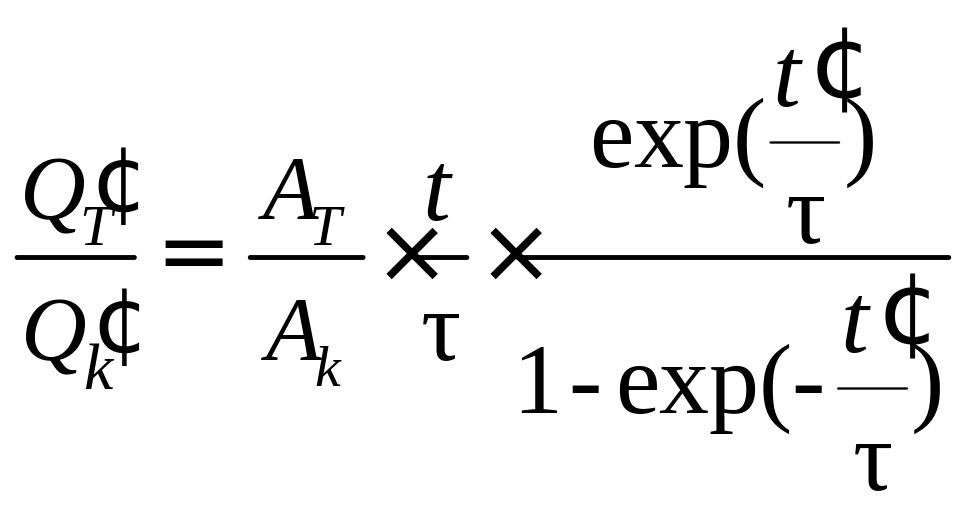
Фильтры

Задачи измерений величин концентрации нуклидов в воздухе решаются различными методами в зависимости от физико-химических свойств аэрозолей. Наиболее широко используемым методом измерений малых концентраций веществ являются реализация явления сорбции на пористых материалах (угли, силикагели и др.); Для аэрозолей с твердыми частицами обычно применяются тканевые материалы (стекловолокно, поливинилхлориды и т.п.), через которые прокачивается исследуемый воздух с аэрозольными радиоактивными частицами. Сконцентрированные на фильтре радиоактивные аэрозоли с целью определения значений активностей, обрабатываются различными радиометрическими методами.

Аэрозольные частицы оседают в фильтре в результате:

● столкновений с волокнами фильтра;

● отклонения от первоначального направления движения, что увеличивает вероятность их захвата;

● электростатического взаимодействия между фильтром и частицами.

При прокачке через фильтр толщиной х воздуха с концентрцией аэрозолей А₀, за фильтром их концентрация снизится до велчины А(х); если аэрозоли одинакового размера, плотность фильтра однородна и скорость прокачки воздуха постоянна, то имеет место соотношение:

,

где k – коэффициент фильтрации, см^-1, зависящий от ряда факторов, основные из которых следующие:

● свойства фильтра;

● форма, размеры и плотность аэрозольных частиц;

● агрегатное состояние частиц;

● концентрация частиц в воздухе;

● скорость прокачки воздуха.

Величина эффективности фильтра η определяется как

,

а величина ε = 1-η – соответствующий коэффициент проскока;

Определение эффективности фильтра может быть реализовано экспериментально методом измерений количества радиоактивных аэрозолей, осажденных в двух идентичных фильтрах при прокачке через них одинакового количества воздуха (рис.кк).

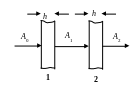
Рис. кк. К определению эффективности фильтра

Для такой геометрии измерений одинаковые эффективности фиьтров η могут быть определены как

,

где Q_1,2 – фиксированные в фильтрах активности, с – константа; из этих отношений следует: и т.к. окончательно

.

Величина проскока ε_n через n параллельных одинаковых фильтров рассчитывается по соотношению:

и, соответственно, .